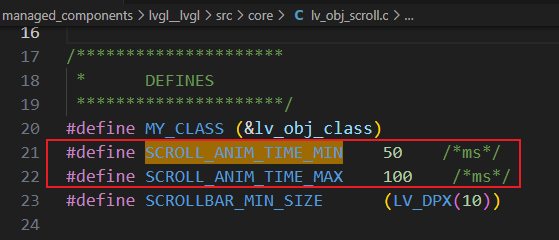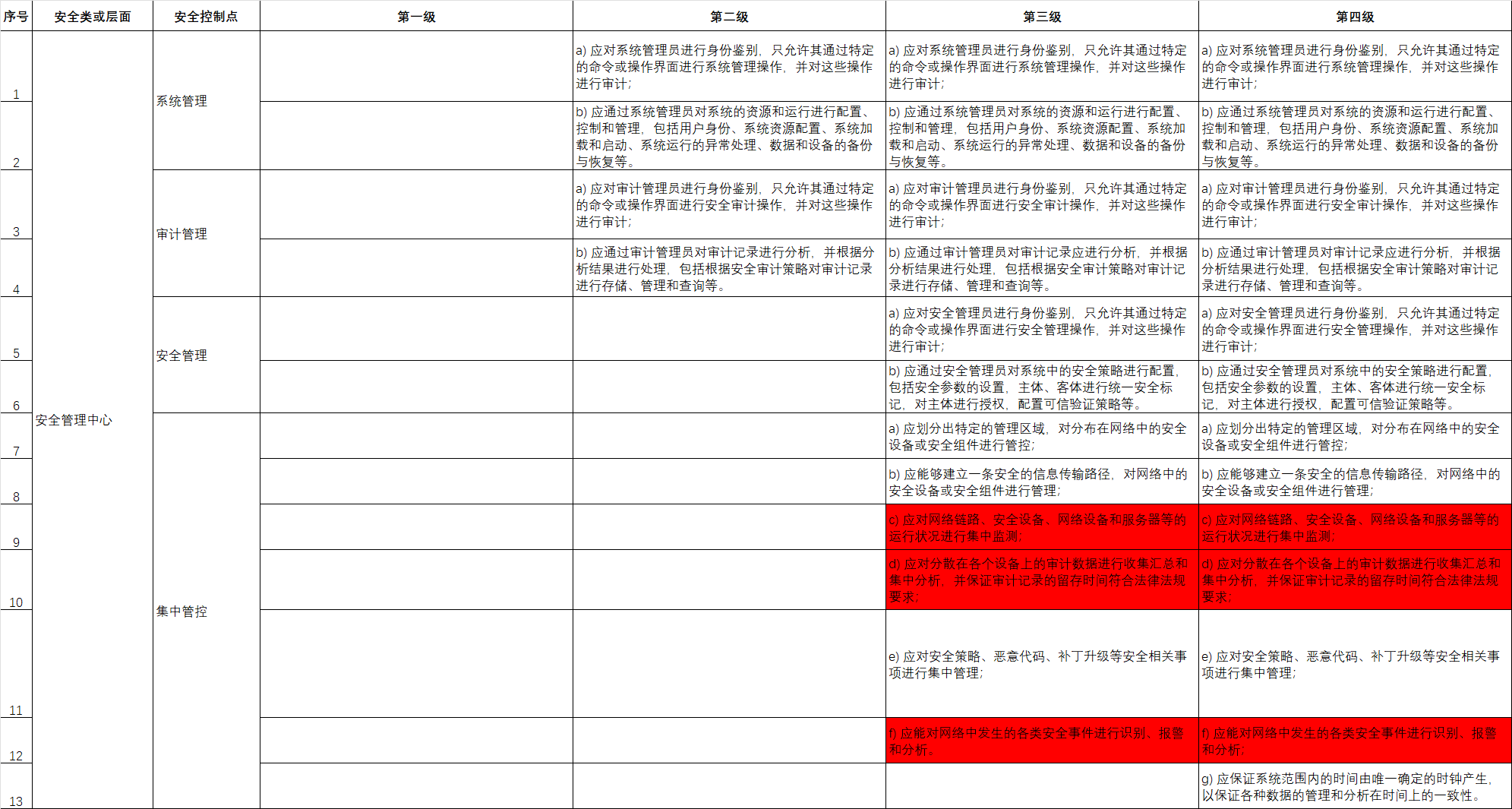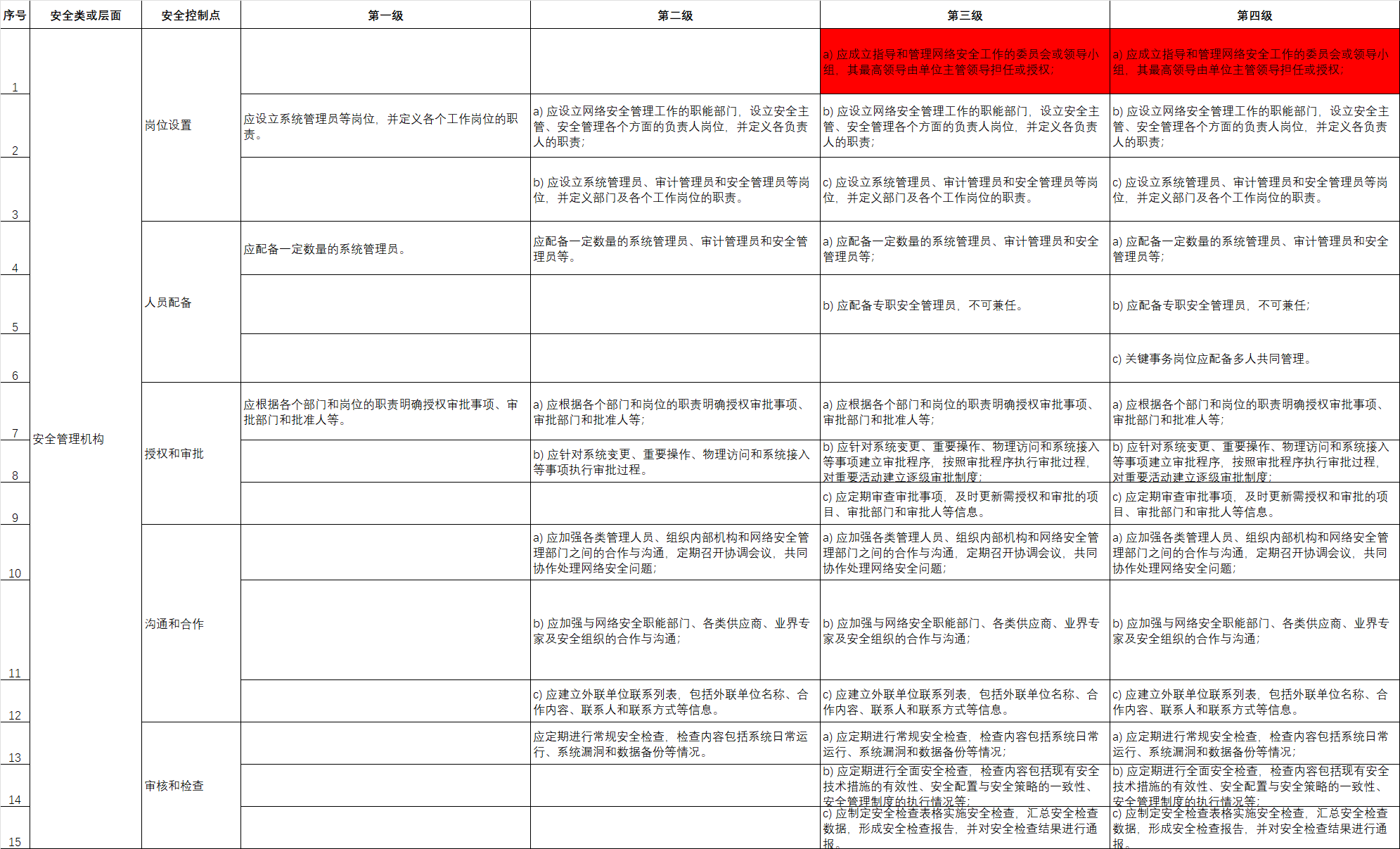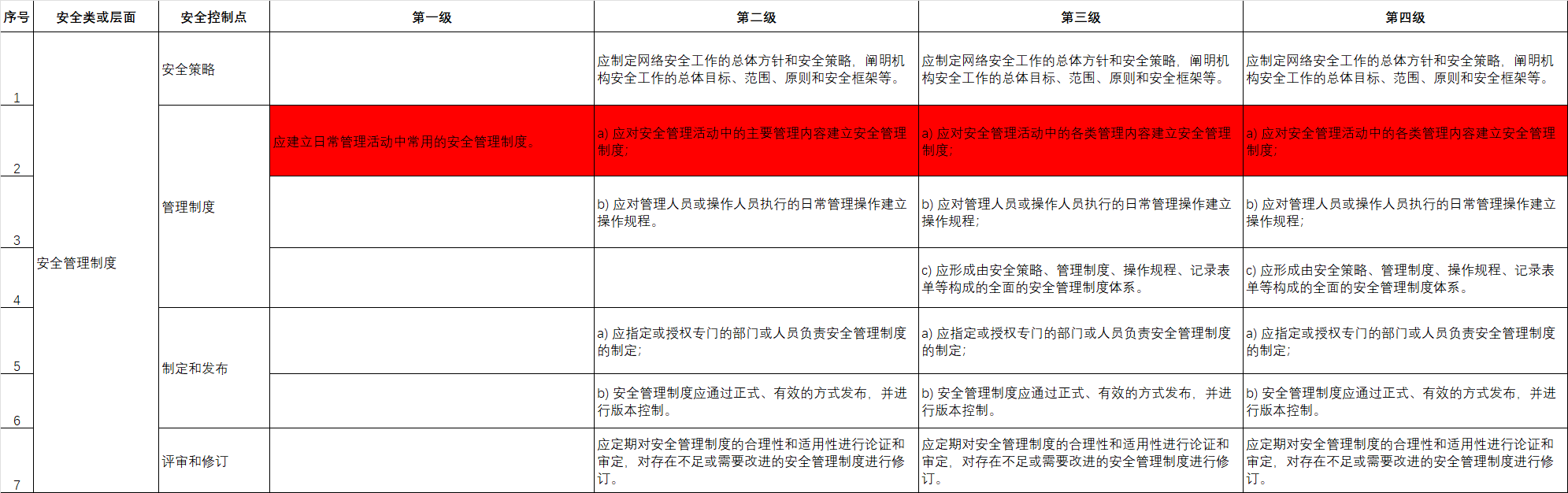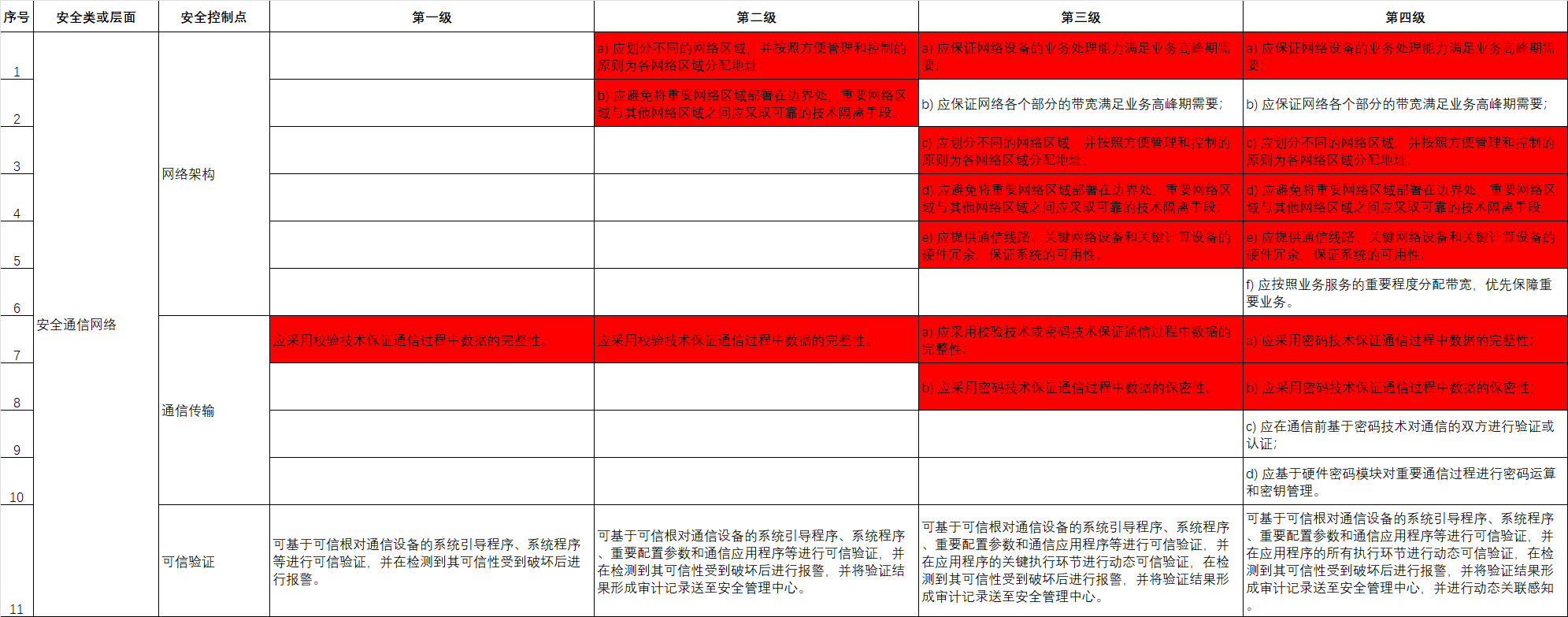
这道题真的做的我鬼火冒,尤其是这个第二问要用到dilworth但是我看讲解完全不知道他们在讲什么,我看了好久才理解,一个数组至少可以由几个不增子序列覆盖就等于严格单调递增的最长子序列的长度,如果是至少可以由几个严格递减子序列覆盖就等于最长单调不减子序列的长度,然后对于第一个问题求最长不增子序列我们将数组中的元素乘以-1,这样就可以求最长不减子序列的长度
要注意的是如果是求严格单调递增子序列用lower_bound,求非严格递增子序列要用upper_bound并且判断该位置是否等于-x如果等于则将该位置后面的一个数变为-x
#include<iostream>
#include<set>
#include<map>
#include<algorithm>
#include<vector>
#include<cmath>
#include<climits>
#include<cstring>
#define int long long
const int N = 1e6+5;
using namespace std;
char* p1, * p2, buf[100000];
#define nc() (p1==p2 && (p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++)
int read()
{int x = 0, f = 1;char ch = nc();while (ch < 48 || ch>57){if (ch == '-')f = -1;ch = nc();}while (ch >= 48 && ch <= 57)x = x * 10 + ch - 48, ch = nc();return x * f;
}
int a[N],b[N];
vector<int>v[N];
signed main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int cnt1 = 0;int cnt2 = 0;int cnt3 = 0;int x;while (cin >> x) {if (!cnt1)a[++cnt1] = -x;else if (-x>=a[cnt1])a[++cnt1] = -x;else {int it = upper_bound(a + 1, a + 1 + cnt1, -x) - a;if (a[it] != -x)a[it] = -x;else a[it + 1] = -x;}if (!cnt2)b[++cnt2] = x;else if (x > b[cnt2])b[++cnt2] = x;else {int it = lower_bound(b + 1, b + 1 + cnt2, x) - b;b[it] = x;}}cout << cnt1 << endl<<cnt2;return 0;
}