这是一篇对 cxy 2025 年同标题集训队论文的分析。该分析会较论文更多地从线性代数角度出发,需要读者有较好的线性代数认识。
基础线性基
考虑在 \(\mathbb{F}_2\) 上定义向量,此时向量加法等价于大整数异或。对于给出的向量组 \(S\),我们希望求出该向量组张成空间(\(\operatorname{span}(S)\))的一个线性基,同时该线性基满足每个向量首个非零元素的位置递减。
求解任意线性空间的线性基可以利用高斯消元做到 \(O(n^3)\) 时间复杂度,但是异或空间可以做到更优。
等价向量组的增量构造
在线性代数中,两个向量组等价当且仅当张成的空间相同,对于给定的向量组 \(S\),和 \(i\neq j\),我们从 \(S\) 中删去 \(S_j\),同时加入 \(S_i\oplus S_j\),得到的新向量组 \(S'\) 和 \(S\) 等价(\(S\cong S'\))。证明考虑原向量组的线性组合,由于向量中的元素全部在 \(\mathbb{F}_2\) 上,因此在线性组合中的系数只需考虑 \(0\) 和 \(1\),对线性组合是否包含 \(S_j\) 分类讨论即可。
接下来给出等价向量组的增量构造。需要构造 \(S'\cong S\),使得 \(S'\) 内的零向量只出现在一段后缀,且非零向量的最高非零位严格递减。假设已经构造出了 \(S'_{1\sim i}\cong S_{1\sim i}\),考虑加入 \(S_{i+1}\),记录指针 \(p=1\),初始令 \(S'_{i+1}=S_{i+1}\),进行讨论,在 \(p=i+1\) 时结束:
-
若 \(S'_{i+1}\) 的最高位高于 \(S'_j\) 的最高位,将 \(S'_{i+1}\) 移到 \(S'_j\) 前,结束整个构造过程。
-
若 \(S'_{i+1}\) 的最高位和 \(S'_j\) 的最高位相同,令 \(S'_{i+1}\leftarrow S'_{i+1}\oplus S'_j\),指针右移。
-
若 \(S'_{i+1}\) 的最高位低于 \(S'_j\) 的最高位,指针右移。
这个过程显然是正确的。考虑最后得到的向量组形如一段非零前缀加上一段全零后缀,此时从极长非零前缀中任取一段子序列,得到的异或和都不相同。不难发现此时这段非零前缀就是原序列的一个线性基,设全零后缀中有 \(c\) 个零向量,则任取 \(2^c\) 中子序列的任意一种异或结果都为零向量。也就是说,原向量组的异或和组成的可重集就是极长非零前缀异或和组成的不可重集复制 \(2^c\) 得到的结果。
线性基的增量构造
上面的过程实际上已经构造出了一个原向量组的线性基(极长非零前缀),时间复杂度为 \(O(|S|m)\),其中 \(m\) 为向量维数,额外空间开销为 \(O(m)\)。
线性基求向量组的最大线性表示
换句话说,就是对于原向量组,找出一个子序列使得异或和最大。
存在简单的贪心过程,考虑线性基 \(w_{0\sim m-1}\)(线性基,\(w_i\) 上存的是最高位为 \(i\) 的向量),从高到低贪心,从 \(ans\oplus w_i\) 和 \(ans\) 中选取较优的一个即可,时间复杂度 \(O(m)\)。
线性基求某个向量被向量组线性表示的方案数
根据上文等价向量组增量构造部分中描述的结论,一个向量被原向量组线性表出的方案数为 \(0\) 或 \(2^c\)。为 \(2^c\) 当且仅当该向量能被线性基线性表出。根据线性代数的经典结论,一个向量能被某个线性无关向量组线性表出当切仅当加入该向量后仍然线性无关,即尝试将该向量插入向量组即可判断能否被线性基线性表出。
线性基求结果小于某个定值的线性表示数量
该问题和求线性基第 \(k\) 小线性表示等强。依然是在线性基上贪心,高位向低位贪心的过程中总是尝试将维护的值和给出的定值变得尽量相等。
线性基解决无向图上最大异或和路径问题
来源:WC2011 最大 XOR 和路径。
给出一张 \(n\) 个点 \(m\) 条边的无向图,找到一条 \(1\rightarrow n\) 的路径(无需简单),使其异或和最大。
考虑一条路径走两次显然不会对答案产生任何影响,因此找到任意一条 \(1\rightarro n\) 的路径,设异或和为 \(v\),存在某一个回路异或和为 \(x\),我们总可以将该回路加入到路径中,即总能选出异或和为 \(v\oplus x\) 的路径,从该路径上的任意一点走到回路再走回来即可。
任取 \(1\rightarrow n\) 的路径,设权值为 \(v\),构造每个回路的异或和张成空间的线性基,答案即为 \(v\) 异或线性基能得到的最大值。
设根据此方法得到的答案为 \(ans'\),真实答案为 \(ans\),\(ans\ge ans'\) 显然。考虑证明 \(ans\le ans'\),设有一条取到 \(ans'\) 的最优路径,则我们先走最优路径到 \(n\),再沿着得到 \(ans'\) 的路径倒着走回 \(1\),再走回 \(n\),前两者是一个回路,因此会被考虑到。
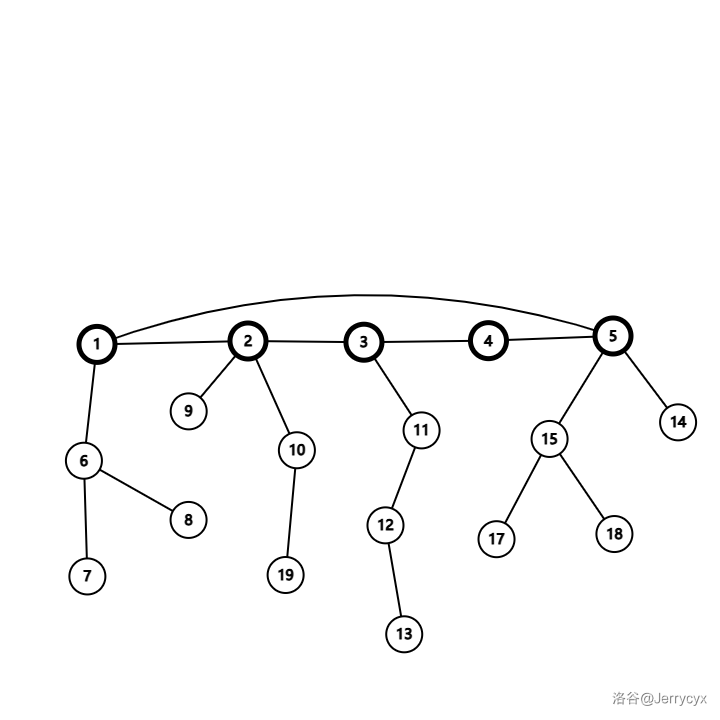
问题此时转化为求所有回路异或和张成空间的线性基,任意求出原图的一棵生成树 \(T\),考虑一条非树边 \((u,v)\),只考虑所有形如 \((u,v)\) 加上 \(uv\) 简单路径这样形态的回路即可。
证明考虑按照该方法得到的线性基 \(basis'\),及原基 \(basis\)。