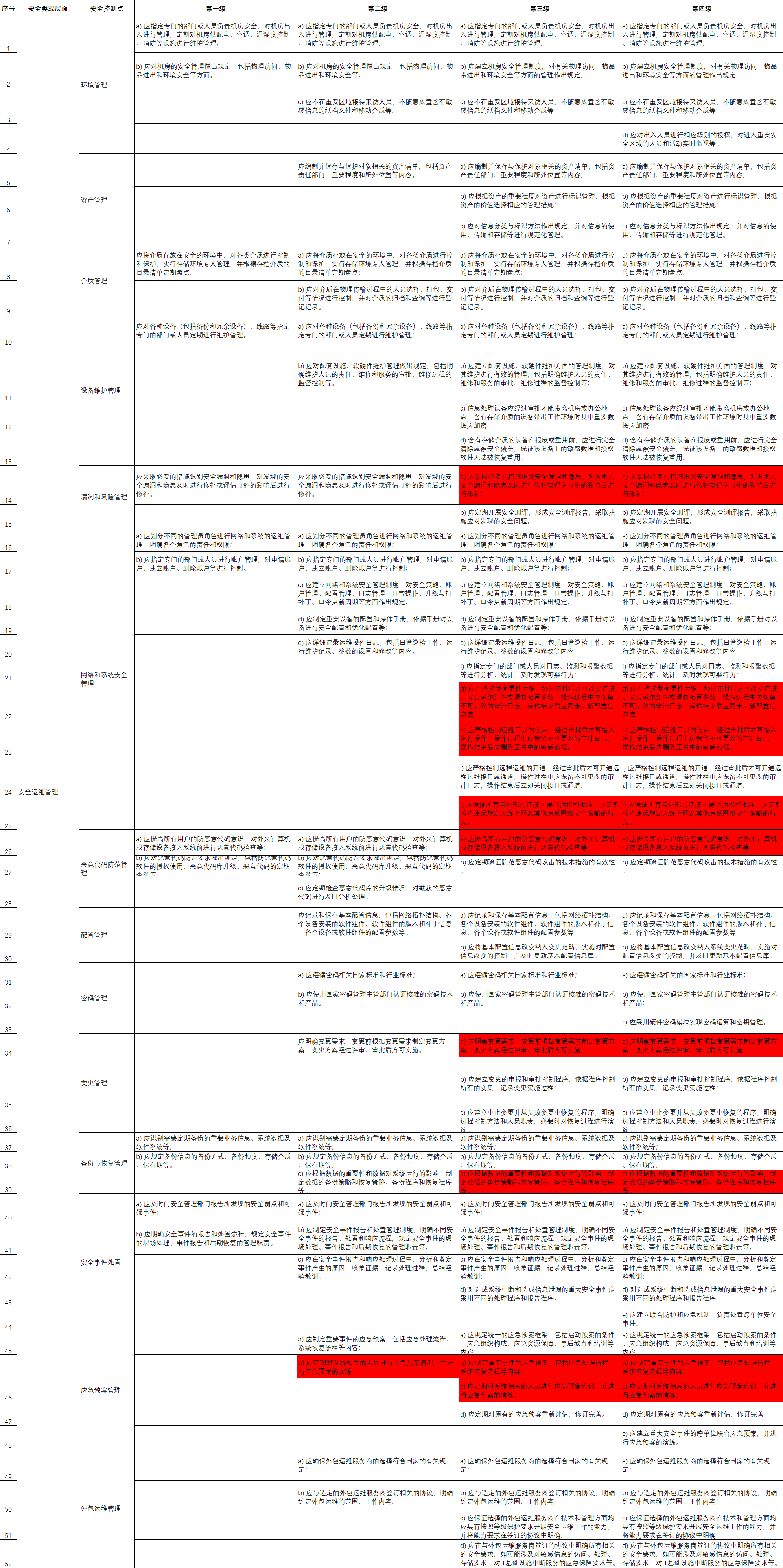
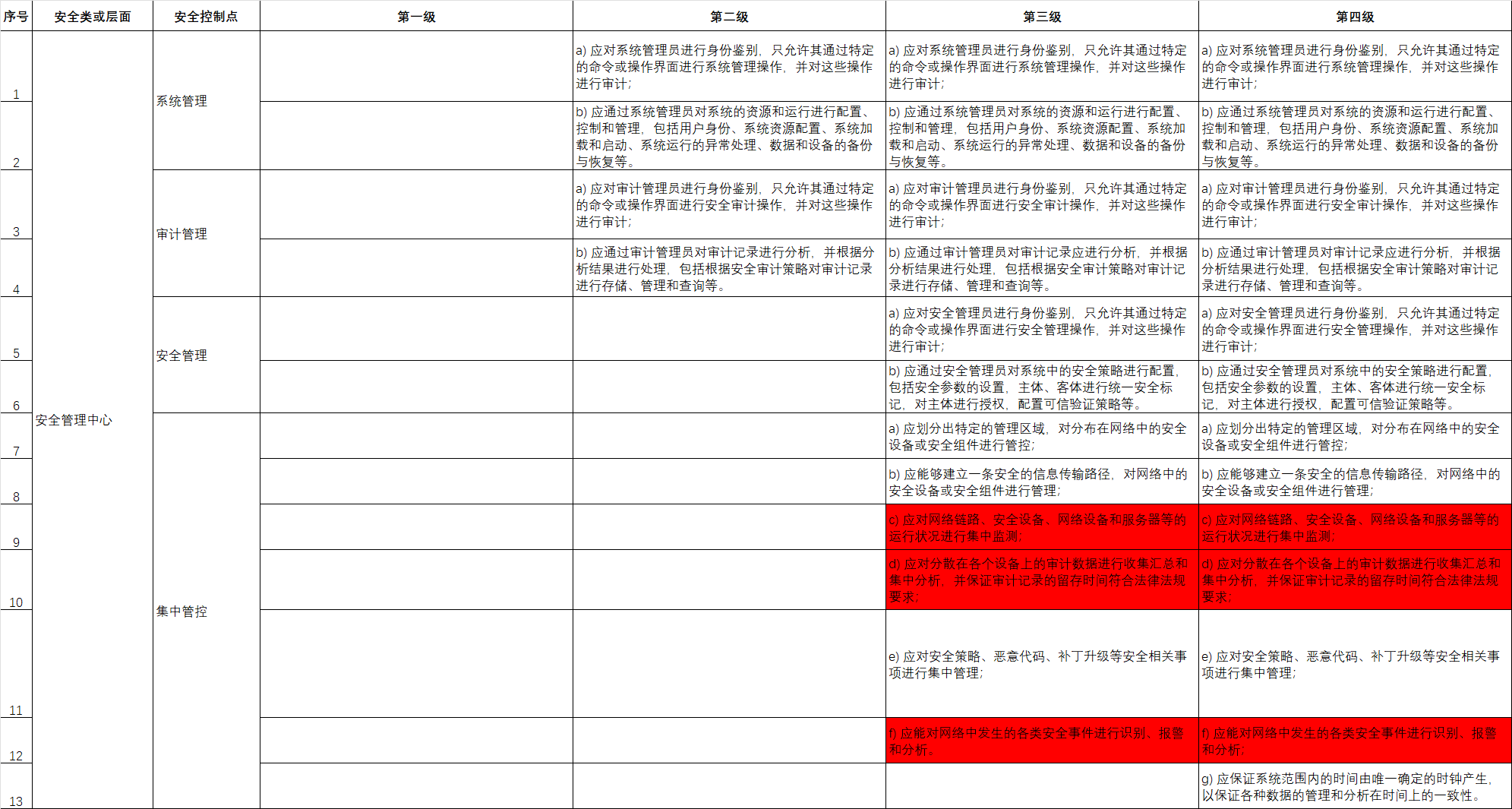
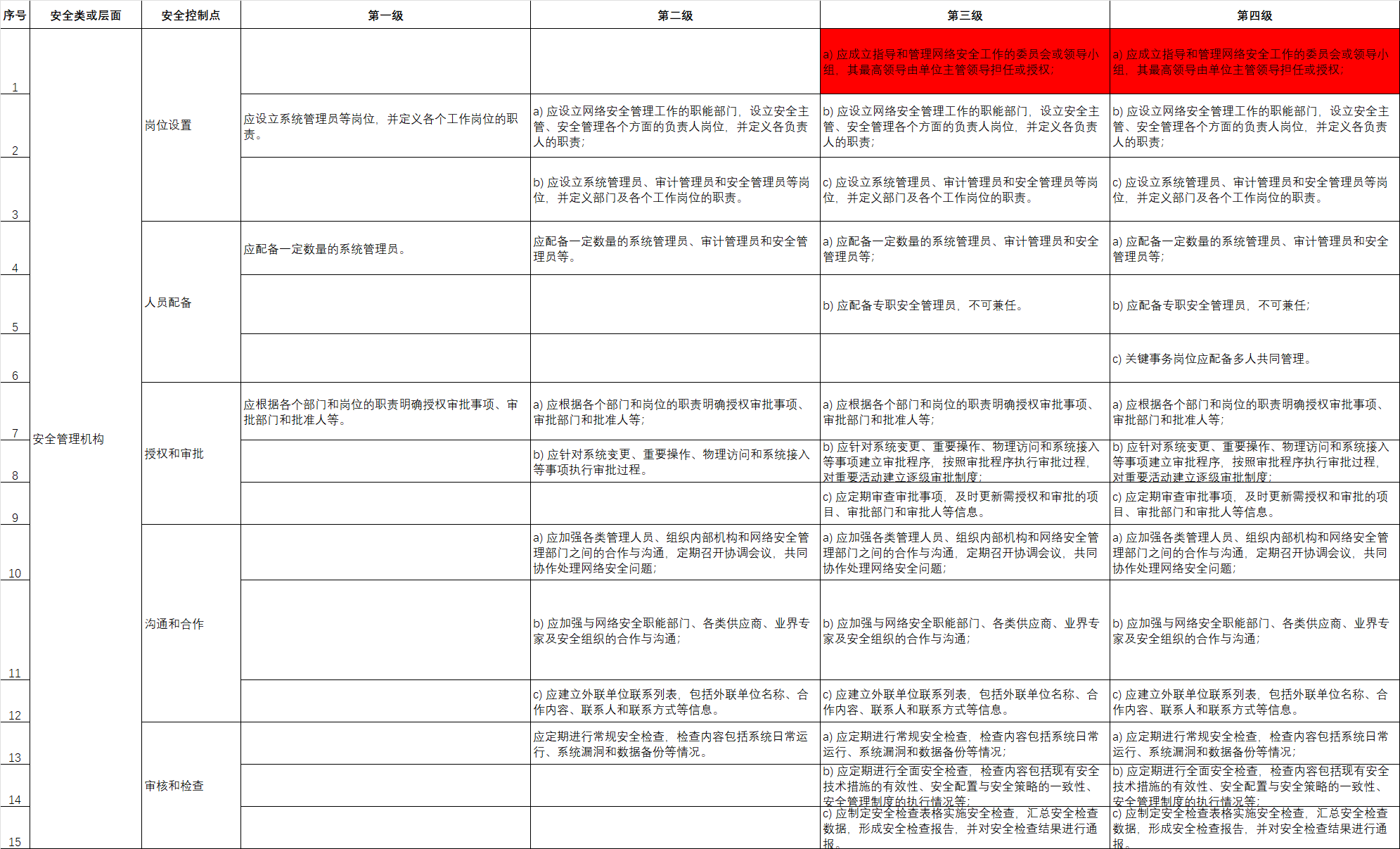
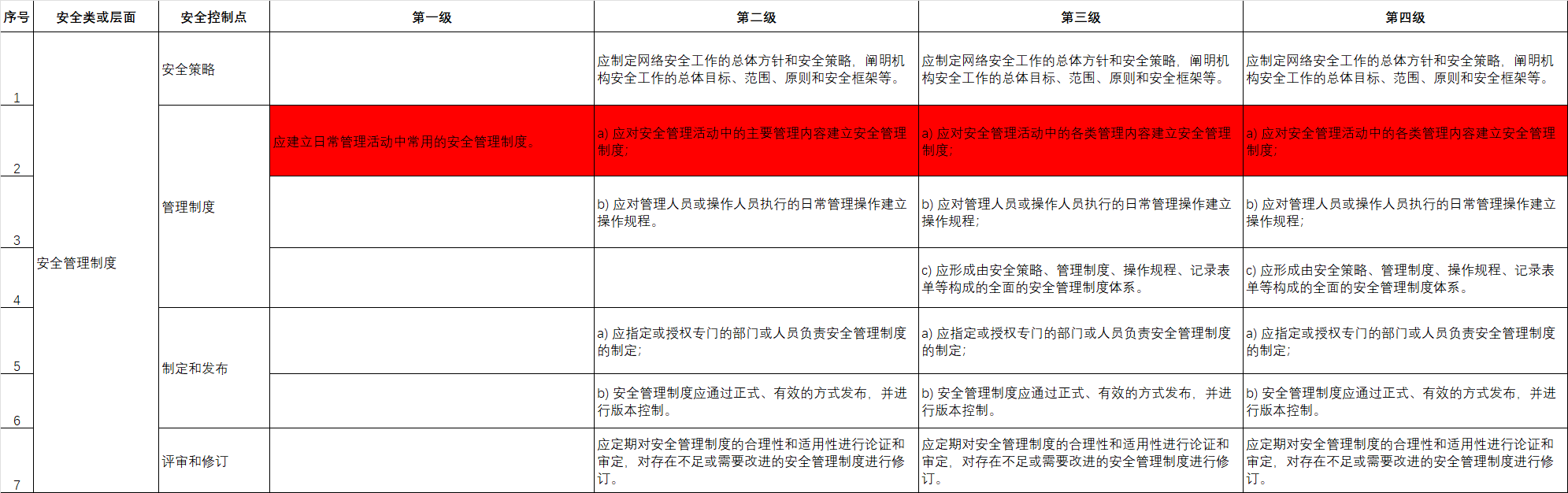
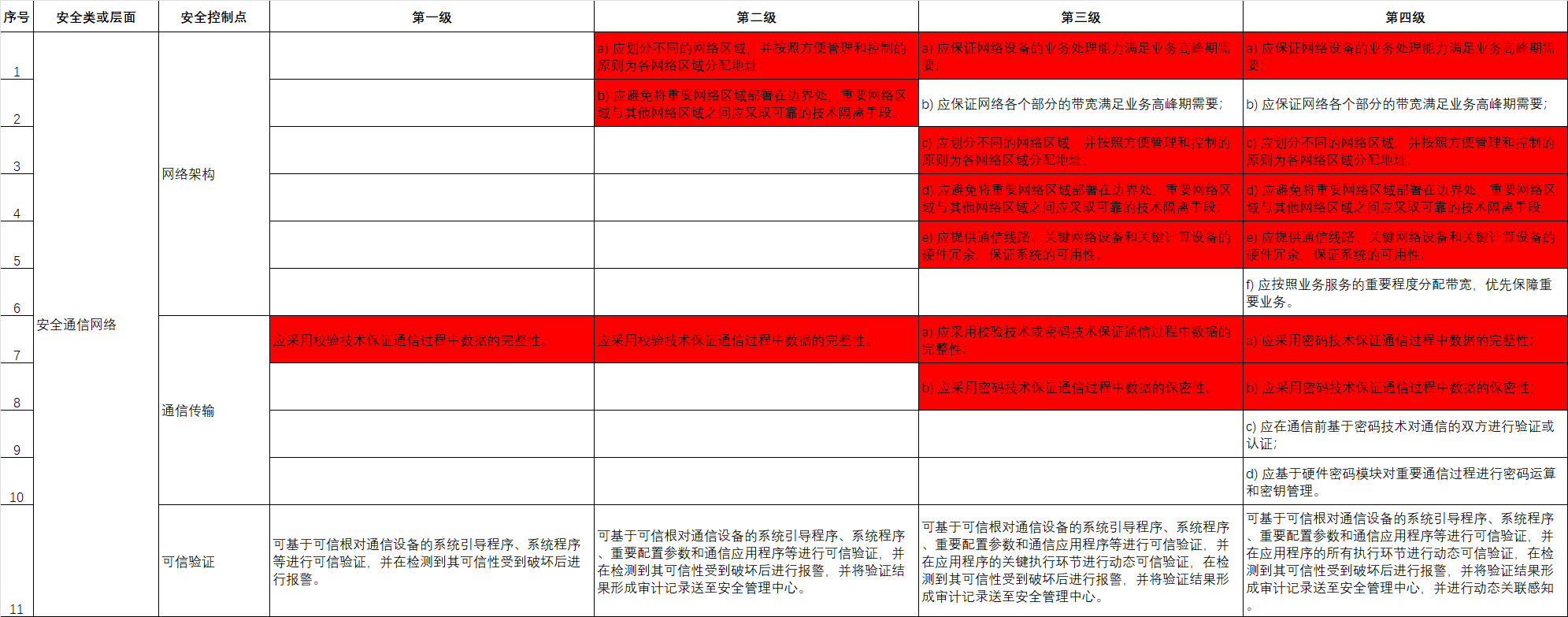
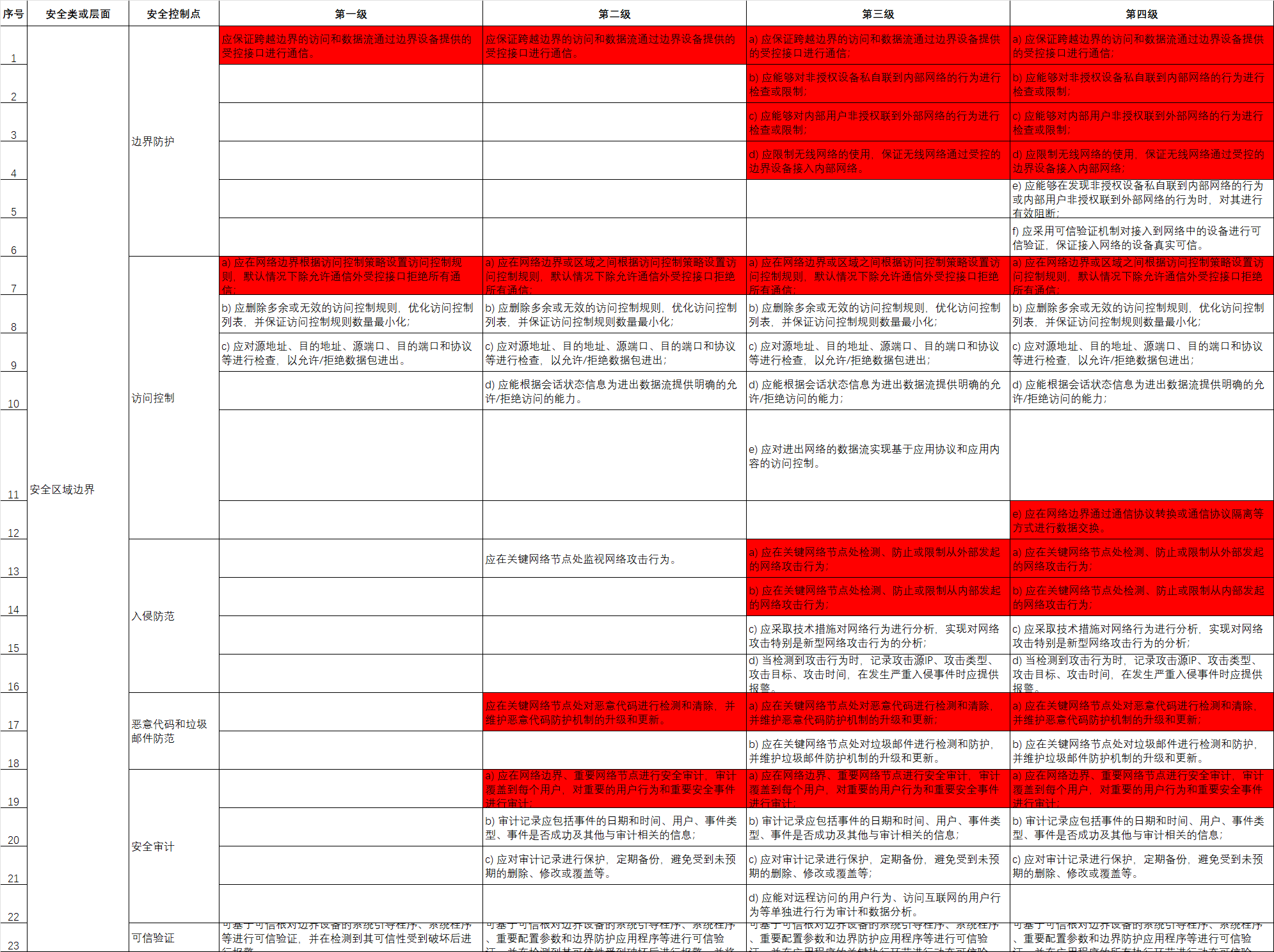
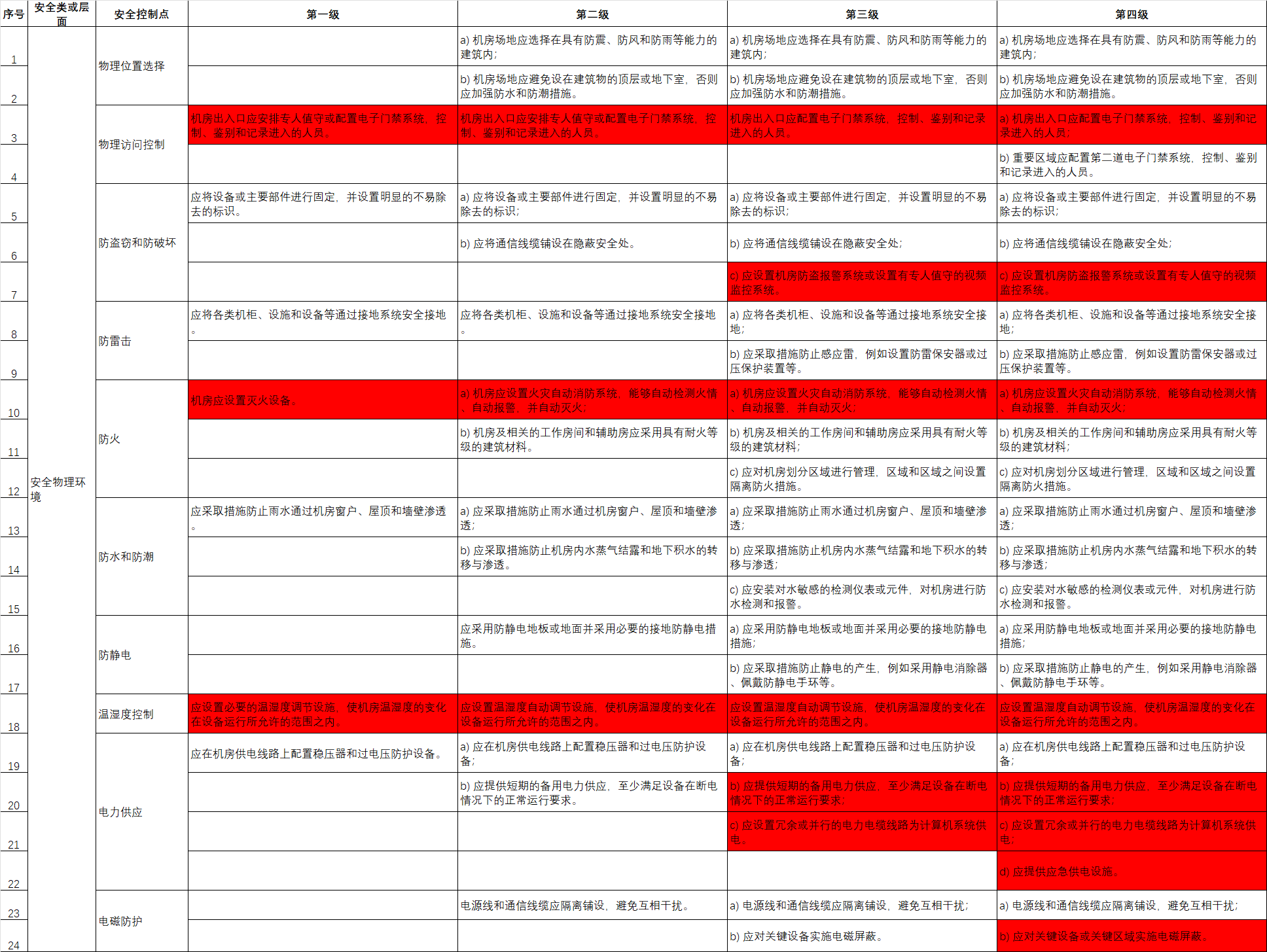
弱透视投影(Weak perspective projection)

弱透视投影是计算机视觉和摄影测量中的一种近似投影模型。在这种投影中,假设物体距离相机足够远,使得物体上各点到相机光心的距离近似相等。
从图中可以看到,有一个光心 \(O\),物体平面上的点 \(P、Q、R\) 等通过光线投影到图像平面上的点 \(p'、q'、r'\)。\(z_0\) 表示物体到相机光心的近似距离,\(f'\) 是相机的焦距。
图中下方的公式展示了弱透视投影的坐标变换关系。原始的透视投影公式为 \(x'=\frac {f'}zx\) 和 \(y'=\frac {f'}zy\) ,在弱透视投影中,由于假设物体各点到相机距离近似为 \(z_0\),所以变换为 \(x'=\frac {f'}{z_0}x\) 和 \(y'=\frac {f'}{z_0}y\) ,我们把 \(\frac {f'}{z_0}\) 叫做放大系数,记为 \(m\)。

在透视投影中,我们可以把变换矩阵 \(M\) 写成 \(M=K[R \ T]=\begin{bmatrix} \mathbf{A} & \mathbf{b} \\ \mathbf{v} & 1 \end{bmatrix}\),而在弱透视投影中,变换矩阵可简化为\(M =\begin{bmatrix} \mathbf{A} & \mathbf{b} \\ \mathbf{0} & 1 \end{bmatrix}\),这种简化基于物体距离相机较远,各点深度近似相等的假设,从而去除了透视投影中与深度相关的复杂计算。

进一步地,在弱透视投影中,由于变换矩阵的最后一行为 \([0,0,0,1]\),因此当我们在计算 \(P'=MP_w\) 的时候,我们能够得到 \(P'=\begin{bmatrix} m_1P_w\\ m_2P_w \\ 1\end{bmatrix}\) ,因此将其化成非齐次坐标的形式,有 \(P'=(m_1P_w,m_2P_w)\),可以认为是对 \(x\) 坐标和 \(y\) 坐标分别进行缩放,这里没有透视除法的步骤,说明弱透视投影具有假设物体深度变化较小,近似平行投影的特性。
正交(仿射)投影(Orthographic (affine) projection)
在这种投影方式下,投影线是相互平行的,且投影线与投影平面是正交的。同时,我们认为投影中心到图像平面的距离无穷远。而一般透视投影公式为\(x' = \frac{f'}{z}x\)和\(y' = \frac{f'}{z}y\) ,其中 \(f'\) 是焦距,\(z\) 是物体点到投影中心的距离。在正交投影中,由于投影中心到图像平面距离无穷远,相当于 \(z\) 趋于无穷大,此时\(\frac{f'}{z}\)趋于0 ,简化后的正交投影公式变为\(x' = x\)和\(y' = y\) ,即物体点的坐标在投影后保持不变。
这些模型的优点
- 弱透视投影(Weak perspective):
- 数学计算简单:相比其他模型,其涉及的数学运算更简便。
- 特定条件下准确:当物体较小且距离较远时,该模型能得出较为准确的结果。
- 适用于识别任务:在目标识别等任务中非常有用。
- 针孔透视投影(Pinhole perspective):
- 3D - 2D映射准确:对于将三维场景映射到二维图像的建模,它的准确性更高。
- 应用领域:常用于运动恢复结构(Structure from Motion,SfM)或同时定位与地图构建(Simultaneous Localization and Mapping,SLAM)等需要精确三维到二维转换的领域。
相机标定( Camera Calibration)
接下来我们介绍的是本节课的重点-相机标定问题。
在前面的介绍中我们已经知道,如果我们要精确描述一个投影变换,我们必须要知道相机的内参矩阵和外参矩阵,而这些矩阵我们都是通过平移旋转等变换得到的,因此为了更好地描述从世界坐标系到图像坐标系的变换,我们需要确定内参矩阵和外参矩阵的相关参数,这一过程我们称为相机标定。
为了更好地对相机标定的过程进行描述,我们这里更换一下解释,用 \(P\) 指代前文的 \(P_w\),用 \(p\) 指代前文的 \(P'\)。

如图所示,这是一个相机标定的基本场景,在世界坐标系中有一个标定板,标定板上有一点 \(P_i\) ,从该点发出的光线射向相机,从而在相机成像平面上形成了投影点 \(p_i\)
因此,如果我们知道了世界坐标系中一些点的位置,并且知道这些点在相机平面形成的投影点的位置,我们就能够确定相机的相关参数。所以相机标定的目标是通过这些已知点在世界坐标系和图像坐标系中的对应关系来求解这些参数进而计算相机的内参和外参。
因为投影矩阵 \(M\) 共有 \(11\) 个自由度,因此需要十一对对应关系精确求解这些参数,这样对吗?
实际上不然,我们只需要使用超过 \(6\) 组对应关系就能够实现这一目标。为什么呢?因为每一对世界坐标系中的点\(P_w\)和图像坐标系中的点\(P'\),通过投影公式\(P' = M P_w\)可以建立2个独立的方程(因为\(P'\)是二维点,\(x\)和\(y\)坐标分别对应一个方程)。例如对于点\(P_w(x_w, y_w, z_w)\)投影到\(P'(x', y')\),有\(x' = \frac{m_{11}x_w + m_{12}y_w + m_{13}z_w + m_{14}}{m_{31}x_w + m_{32}y_w + m_{33}z_w + m_{34}}\)和\(y' = \frac{m_{21}x_w + m_{22}y_w + m_{23}z_w + m_{24}}{m_{31}x_w + m_{32}y_w + m_{33}z_w + m_{34}}\)(这里\(m_{ij}\)是投影矩阵\(M\)的元素),在齐次坐标转换后可得到2个独立方程。
那么6对对应点就可以提供\(6×2 = 12\)个方程,理论上足以求解上述11个独立参数。
接下来我们介绍如何进行标定。
假设我们知道了三维点 \(P_i\),由投影变换公式 \(p_i=MP_i\),我们可以得到它投影到二维点的坐标为 \(\begin{bmatrix} \frac{m_1P_i}{m_3P_i}\\ \frac{m_2P_i}{m_3P_i}\end{bmatrix}\),同时因为我们知道在图像平面上点 \(p_i\) 的坐标为 \(\begin{bmatrix} u_i\\ v_i\end{bmatrix}\),因此我们能够建立等式 \(\begin{bmatrix} u_i\\ v_i\end{bmatrix}=\begin{bmatrix} \frac{m_1P_i}{m_3P_i}\\ \frac{m_2P_i}{m_3P_i}\end{bmatrix}\),这其实是两个等式,即 \(u_i=\frac{m_1P_i}{m_3P_i}\) 和 \(v_i=\frac{m_2P_i}{m_3P_i}\),我们对这两个式子进行化简,有:\(u_i(m_3P_i)=m_1P_i\) 和 \(v_i(m_3P_i)=m_2P_i\) 整理一下得到 \(u_i(m_3P_i)-m_1P_i=0\) 和 \(v_i(m_3P_i)-m_2P_i=0\)

我们把 \(n\) 组对应点 \(2n\) 个对应关系组合在一起,其实要解决的就是一个方程组的问题了,如图所示。

但是这一方程组我们没有办法直接进行求解,有没有什么办法能够让它的形式更加简单呢?我们擅长求解的是齐次线性方程组,有没有什么办法将其化简成齐次线性方程组呢?
观察上述式子,如果我们对其左右两边各乘上一个负号,每一个式子都可以看做是由相乘的两部分相加的形式,这与什么很类似呢?矩阵乘法!如图所示:

因此,我们可以把以上的方程紧凑地表示为 \(\mathbf{Pm}=0\),其中\(\mathbf{P}\)是一个\(2n \times 12\)的矩阵,其构造方式为:
\(
\mathbf{P} =
\begin{pmatrix}
\mathbf{P}_1^T & \mathbf{0}^T & -u_1\mathbf{P}_1^T \\
\mathbf{0}^T & \mathbf{P}_1^T & -v_1\mathbf{P}_1^T \\
\vdots & \vdots & \vdots \\
\mathbf{P}_n^T & \mathbf{0}^T & -u_n\mathbf{P}_n^T \\
\mathbf{0}^T & \mathbf{P}_n^T & -v_n\mathbf{P}_n^T
\end{pmatrix}
\),这里,\(\mathbf{P}_i^T\)是世界点\(P_i\)的转置,\(\mathbf{0}^T\)是零向量的转置。
\(\mathbf{m}\)是一个\(12 \times 1\)的向量,定义为:\( \mathbf{m} = \begin{pmatrix} \mathbf{m}_1^T \\ \mathbf{m}_2^T \\ \mathbf{m}_3^T \end{pmatrix} \),其中\(\mathbf{m}_1^T,\mathbf{m}_2^T,\mathbf{m}_3^T\)分别是投影矩阵\(M\)行向量的转置。
由于我们知道了每一个世界点的相关信息,相当于整个 \(P\) 矩阵我们都是知道的,因此我们是在 \(P\) 已知的情况下要求解 \(m\) 矩阵。
我们把上述问题称为齐次线性系统,即线性系统可表示为 \(\mathbf{Pm}=0\),其中 \(\mathbf{P}\) 是 \(M×N\) 的矩阵(在相机标定中由已知的世界点和图像点坐标构成),\(m\) 是包含 \(N\) 个未知参数的向量(对应投影矩阵的未知参数)。在该线性系统下,零向量总是它的一个解,但由于零向量显然对于我们标定相机没有帮助,我们仍然需要重新寻找一个非零解,并且该非零解需要满足在 \(|m|^2=1\) 的情况下 \(|Pm|^2\) 最小。
为了解决这一问题,我们采用 SVD 分解法。
通过 SVD 分解,我们能够将 \(\mathbf{P}\) 分解为三个矩阵的乘积形式:\(\mathbf{P} = \mathbf{U}_{2n \times 12} \mathbf{D}_{12 \times 12} \mathbf{V}_{12 \times 12}^T\) 。其中:
- \(\mathbf{U}\)是一个\(2n \times 12\)的矩阵。
- \(\mathbf{D}\)是一个\(12 \times 12\)的对角矩阵,对角元素为\(\mathbf{P}\)的奇异值。
- \(\mathbf{V}\)是一个\(12 \times 12\)的正交矩阵。
则向量 \(\mathbf{m}\) 可以由矩阵 \(\mathbf{V}\) 的最后一列得到,原理这里不过多进行赘述。得到 \(m\) 矩阵后,我们就能进一步确定变换矩阵 \(M\)。

进一步地,我们知道了变换矩阵 \(M\),我们就能够确定内参矩阵和外参矩阵中的相关参数。

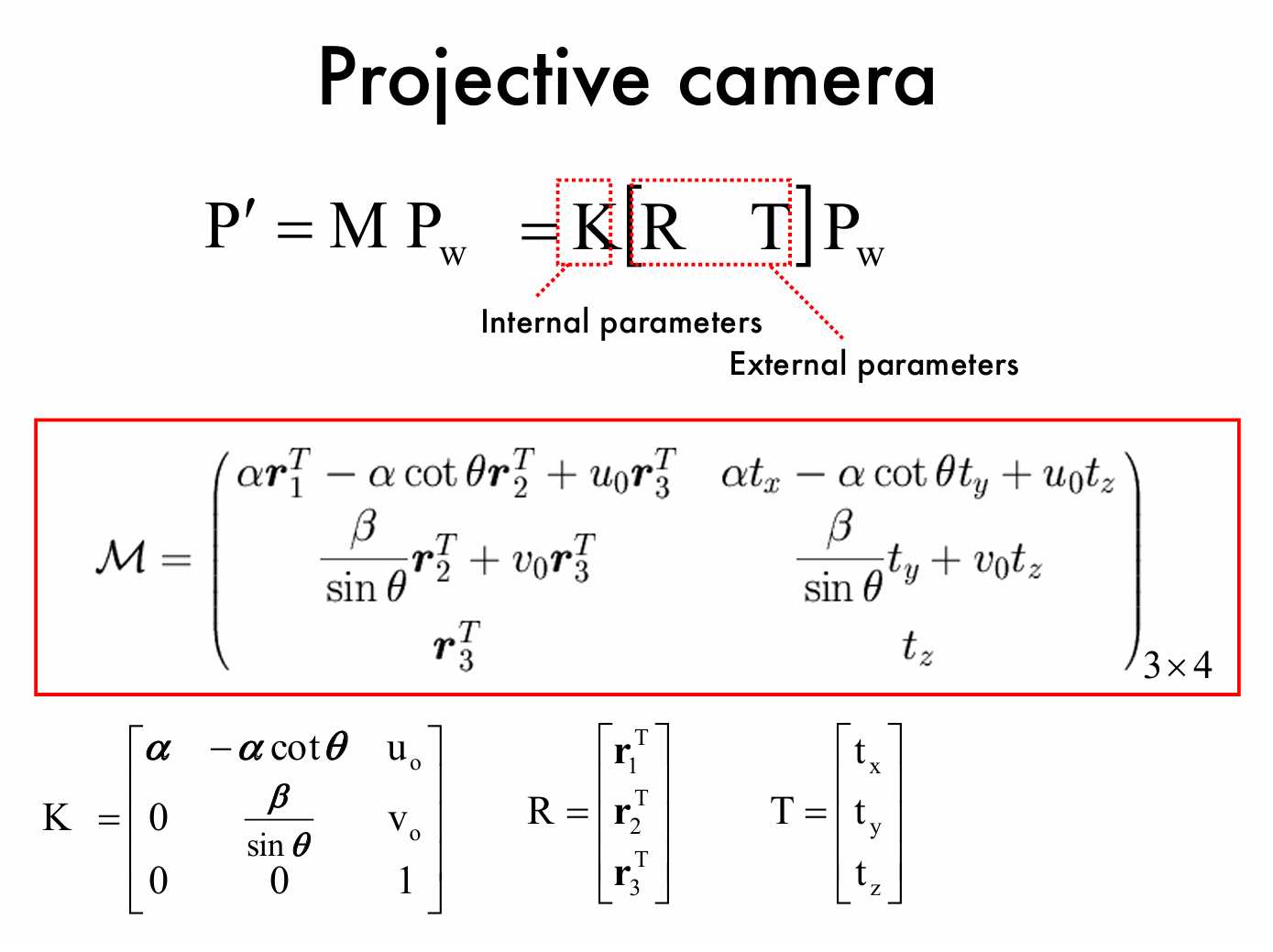
如图所示,我们先给出相机投影矩阵 \(M\) 除以尺度因子 \(\rho\) 后的形式 \(\frac{M}{\rho}\),并将其分块为矩阵 \(A\) 和向量 \(\mathbf{b}\) 两部分:
\(\frac{M}{\rho}=\begin{pmatrix}
\alpha \mathbf{r}_1^T - \alpha \cot\theta \mathbf{r}_2^T + u_0 \mathbf{r}_3^T & \alpha t_x - \alpha \cot\theta t_y + u_0 t_z \\
\frac{\beta}{\sin\theta} \mathbf{r}_2^T + v_0 \mathbf{r}_3^T & \frac{\beta}{\sin\theta} t_y + v_0 t_z \\
\mathbf{r}_3^T & t_z
\end{pmatrix} =
\begin{pmatrix}
A & \mathbf{b}
\end{pmatrix}
\)
其中,\(A\) 是 \(3\times3\) 矩阵,\(\mathbf{b}\) 是 \(3\times1\) 向量。
进一步,我们将矩阵 \(A\) 按行表示为 \(\mathbf{a}_1^T\)、\(\mathbf{a}_2^T\)、\(\mathbf{a}_3^T\),向量\(\mathbf{b}\) 按行表示为 \(\mathbf{b}_1\)、\(\mathbf{b}_2\)、\(\mathbf{b}_3\) ,即 \(A = \begin{bmatrix} \mathbf{a}_1^T \\ \mathbf{a}_2^T \\ \mathbf{a}_3^T \end{bmatrix}\),\(\mathbf{b} = \begin{bmatrix} \mathbf{b}_1 \\ \mathbf{b}_2 \\ \mathbf{b}_3 \end{bmatrix}\) ,这些是估计值。
则我们能够提取出相机参数的公式:
-
尺度因子\(\rho = \frac{\pm1}{|\mathbf{a}_3|}\) 。
-
图像主点坐标\(u_0 = \rho^2 (\mathbf{a}_1 \cdot \mathbf{a}_3)\),\(v_0 = \rho^2 (\mathbf{a}_2 \cdot \mathbf{a}_3)\) 。
-
像素纵横比角度参数\(\theta\)的余弦值\(\cos\theta = \frac{(\mathbf{a}_1 \times \mathbf{a}_3) \cdot (\mathbf{a}_2 \times \mathbf{a}_3)}{|\mathbf{a}_1 \times \mathbf{a}_3| \cdot |\mathbf{a}_2 \times \mathbf{a}_3|}\) 。
从而,我们可以得到下图中的重要参数:
内参矩阵

外参矩阵

因此相机标定的工作我们就完成了,我们只需要把上述求得的参数带回我们的内参矩阵和外参矩阵即可,这里我们把最初的定义再放一遍:

退化情况
假如世界坐标系中的点共面,会导致标定过程中的约束不足,使得无法准确求解相机的内参和外参等参数。同时,如果点位于两个二次曲面的交线上。这也会引起标定退化的情况,同样会造成参数求解的困难或不确定性。
因此在相机标定的过程中,我们应该避免这两种情况。
带有径向畸变的相机标定(Camera calibration with radial distortion)
首先我们先介绍一下什么是径向畸变。由于图像放大率随着与光轴距离的增加而减小(或增大),但是镜头不完善,图像会产生偏差,对于通过镜头边缘的光线,其偏差最为明显。
有三种不同的畸变类型:
\(\bullet\) 无畸变(No distortion):方格图案保持规则的矩形。
\(\bullet\) 枕形畸变(Pin cushion):方格图案向外凸起,边缘部分向外拉伸。
\(\bullet\) 桶形畸变(Barrel):方格图案向内凹陷,边缘部分向内收缩。

由于径向畸变,我们需要对之前的投影变换进行修正,即在公式前乘上一个缩放矩阵 \(\begin{pmatrix} \frac1\lambda & 0 &0\\ 0 & \frac1\lambda &0\\ 0 & 0 &0 \end{pmatrix}\),该缩放矩阵只有一个重要参数 $\lambda $,而 $\lambda = 1 \pm \sum_{p = 1}^{3} \kappa_p d^{2p} $ ,其中\(\kappa_p\)是畸变系数,\(d^2 = a u^2 + b v^2 + c u v\) \(d\)是图像点到光心的距离。该公式是一个多项式函数,用于建模径向畸变行为,通过调整\(\kappa_p\)的值来描述不同程度和类型的径向畸变。同时该模型根据点的不同位置精确地模拟了通过镜头边缘的光线,其偏差最为明显,效果较好。
我们将缩放矩阵与变换矩阵相乘得到的矩阵记为 \(Q\),即 \(Q=\begin{pmatrix} \frac1\lambda & 0 &0\\ 0 & \frac1\lambda &0\\ 0 & 0 &0 \end{pmatrix}M\),如果我们把 \(Q\) 矩阵进行分块,即 \(Q=\begin{pmatrix} q_1 \\ q_2 \\ q_3 \end{pmatrix}\),由因为我们知道图像上点的坐标,那我们就有:\(p_i=\begin{bmatrix} u_i\\ v_i\end{bmatrix}=\begin{bmatrix} \frac{q_1P_i}{q_3P_i}\\ \frac{q_2P_i}{q_3P_i}\end{bmatrix}\),从而能够得到 \(u_i(q_3P_i)=q_1P_i\) 和 \(v_i(q_3P_i)=q_2P_i\) 。
那后面的做法与之前一样吗?当然不是。主要的原因是我们得到的等式不是一个线性系统,不能简单地利用线性方法对其进行求解。我们这里要求解的问题是形如 \(X=f(Q)\) 的问题,其中 \(X\) 代表测量值(图像坐标),\(Q\) 是缩放矩阵与变换矩阵相乘的结果,\(f\) 是非线性映射函数。
解决非线性问题我们一般有两种做法:
牛顿法(Newton Method):是一种迭代方法,需要从初始解开始。其缺点包括如果初始解离真实解较远,求解过程可能较慢;并且由于存在局部极小值,估计解可能依赖于初始解。此外,牛顿法需要计算雅可比矩阵 \(J\) 和海森矩阵 \(H\)。
列文伯格 - 马夸尔特算法(Levenberg - Marquardt Algorithm):同样是迭代方法,从初始解开始。相比牛顿法,它的优势在于不需要计算海森矩阵 \(H\),在一定程度上降低了计算复杂度。
下面介绍一种可能算法。步骤为:先求解系统线性部分找近似解;将此解作为完整系统初始条件;用牛顿法或列文伯格 - 马夸尔特算法求解完整系统。此算法利用先线性求解得初值再处理非线性部分的思路来应对相机标定的非线性问题。
从以上可以看出,在相机标定中,一些假设在实际应用中可以使相机标定问题变得相对简单,但同时也可能会在一定程度上影响标定的准确性,需要根据具体情况进行权衡和调整。通常我们会做出以下的假设:
-
零倾斜,方形像素:即假设图像像素之间不存在倾斜关系,并且像素是正方形的。这简化了相机内参的模型,减少了需要估计的参数数量。
-
\(u_0,v_0\)为已知的图像中心:假设图像的主点坐标 \(()\) 是已知的,通常可以简单地认为是图像的几何中心。这个假设也有助于简化相机标定过程中的计算。
可以看出,在径向畸变的情况下,我们求解标定相机还是非常困难的,那么在某些情况下我们是否能够忽略径向畸变,从而较为简单地求解问题呢?
事实上,我们可以利用 \(\frac{u_i}{v_i}\),也就是斜率帮助我们简化问题。

首先给出图像点坐标 \(p_i = \begin{bmatrix}u_i \\ v_i\end{bmatrix}\) 与世界坐标系中的点 \(P_i\) 以及矩阵向量 \(\mathbf{m}_1\)、\(\mathbf{m}_2\)、\(\mathbf{m}_3\)的关系公式:
$ p_i = \begin{bmatrix}
u_i \
v_i
\end{bmatrix} = \frac{1}{\lambda} \begin{bmatrix}
\frac{\mathbf{m}_1 P_i}{\mathbf{m}_3 P_i} \
\frac{\mathbf{m}_2 P_i}{\mathbf{m}_3 P_i}
\end{bmatrix}$,进一步能够得到 \(\frac{u_i}{v_i} = \frac{\frac{\mathbf{m}_1 P_i}{\mathbf{m}_3 P_i}}{\frac{\mathbf{m}_2 P_i}{\mathbf{m}_3 P_i}} = \frac{\mathbf{m}_1 P_i}{\mathbf{m}_2 P_i}\) ,从而有 \(v_i(m_1P_i)-u_i(m_2P_i)=0\)。
我们将方程组合到一起得到方程组,这组方程可写成矩阵形式\(L\mathbf{n} = 0\),其中\(L\)是由图像点坐标和世界点坐标构成的矩阵,\(\mathbf{n} = \begin{bmatrix}\mathbf{m}_1^T \\ \mathbf{m}_2^T\end{bmatrix}\) 。通过对矩阵\(L\)进行奇异值分解(SVD),可以求解得到 \(\mathbf{m}_1\)和\(\mathbf{m}_2\) 。
但是这种做法只能计算出 \(\mathbf{m}_1\)和\(\mathbf{m}_2\),而 \(\mathbf{m_3}\) 不能通过简单的线性关系得出,后续估计或计算时需要考虑其非线性特性。
以上就是本节课的所有内容,如有问题,请指正。