串串全家桶

Manacher

用途：

该算法可在 \(O(n)\) 的时间复杂度下求出以每一个点（和缝，即回文串长为偶数的情况）为中心的最长回文串长度。

做法：

前置：定义朴素算法为，对于每一个点为中心的情况，暴力枚举是否可以扩展两边，直到不能扩展，此时得到结果。
代码如下，其中 \(a\) 是字符数组， \(x\) 是我们计算的中心，而 \(ans_x\) 则是答案。

while(a[x-ans[x]-1]==a[x+ans[x]+1])++ans[x];

1. 预处理：在原串的 \(n+1\) 个缝里插入任意不在原串中的字符，在首和尾再插入两种与之前不同的字符
   举个例子，若原串是 abcdefg ，一种合法的预处理方式是 @#a#b#c#d#e#f#g#$ 。插入的三种字符互不相同。
   在这个例子中，插入 # 的原因是显然的，如果我们有 a#a ，我们就可以计算出原串中长度为 \(2\) 的回文串。
   插入 @ $ 的原因是将他们作为哨兵，他们不可能被包含在回文串中，所以扫到它们的时候我们可以不用特判而知道停止扫描。
2. 处理 \(ans\) ：假设我们在处理位置 \(i\) 前已经处理出了 \(ans_{1\sim i-1}\) ，我们维护当前最右的被之前的回文串包住的位置为 \(r\)，则若 \(r<=i\)，则我们直接对该位置做朴素算法；否则，我们可以给 \(ans_i\) 赋上一个初值，从而减少重复的枚举。
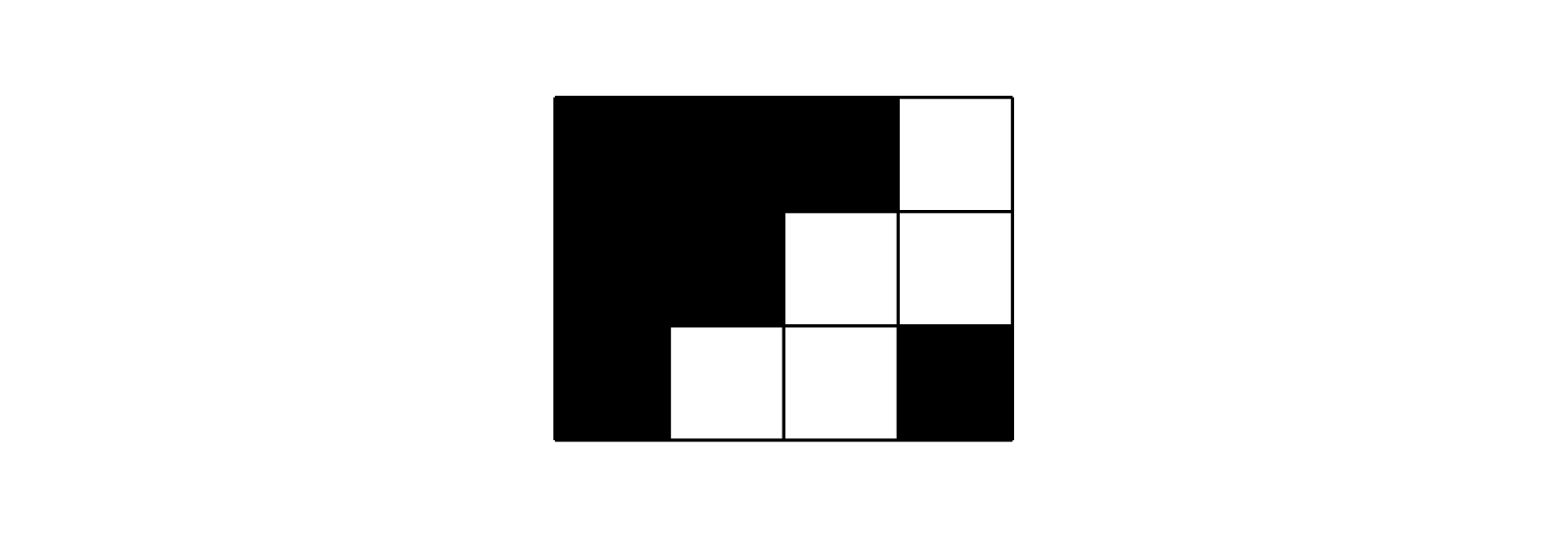
   若使得 \(r\) 最大的位置为 \(p\) ，则我们可以把 \(i\) 关于 \(p\) 对称的位置的 \(ans\) 赋给 \(i\)，给出一张图来解释原因。
   
   但是，我们不难发现，这个好像只在 \(p\) 的回文串包含 \(i'\) 时才成立，如果是下图的情况，我们简单分析可以发现初值应为 \(r-i\) ，因为我们并不能保证两绿色段拼上后合法。
   

由此我们做完了。

复杂度分析

$case_1: i\ge r $ 此时，朴素算法拓展次数等于 \(r\) 的增量。
$case_2: i<r \wedge $ 回文串范围被 \(r\) 覆盖 此时 \(ans_i\) 初值等于末值，朴素算法执行 \(1\) 次。
$case_3: i<r \wedge $ 回文串范围未被 \(r\) 覆盖 此时 \(i+ans_i\) 初始 \(=r\) ，朴素算法拓展次数等于 \(r\) 的增量。
由于 \(r\) 最多被增加 \(n\) 次，所以该算法复杂度为 \(O(n)\) 。

code

int r,nid;
void calc(int x)
{while(a[x-ans[x]-1]==a[x+ans[x]+1])++ans[x];if(r<x+ans[x]){r=x+ans[x];nid=x;}
}
for(int i=1;i<=tp;i++)
{if(i<=r){ans[i]=min(ans[nid*2-i],r-i);}calc(i);
}