卡特兰数学习笔记

引入

从 \((0,0)\) 走到 \((n,n)\)，求不越过 \(y=x\) 的方案数。

不考虑是否合法的方案数是 \(\binom{2n}{n}\)，即从 \(2n\) 个移动中选 \(n\) 个向右的。

接下来考虑不合法的情况，不合法当且仅当碰到了 \(y=x+1\) 这条直线，设这个点是 \((p,p+1)\)，将后面的折线沿着 \(y=x+1\) 翻折。

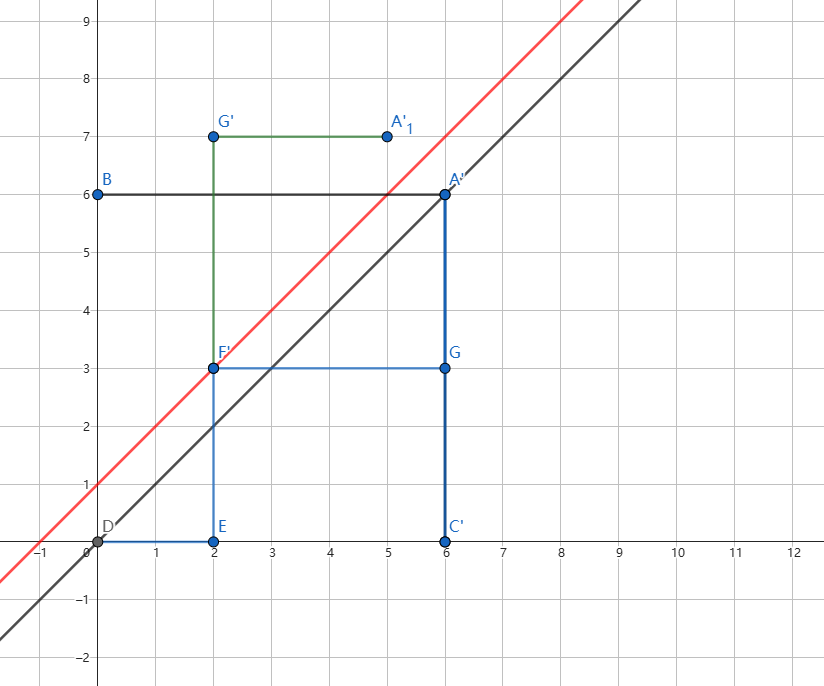
从图中不难看出，不合法路径的终点翻折后变成了 \((n-1,n+1)\)，因为这是 \(A\) 的对称点。于是所有不合法的路径数量就是从 \((0,0)\) 走到 \((n-1,n+1)\) 的方案数，因为二者是一一对应关系。

最终的答案就成了 \(\binom{2n}{n} - \binom{2n}{n+1}\)。

卡特兰数

上个例子的答案就是卡特兰数的定义。OEIS 上的 卡特兰数。

接下来介绍卡特兰数的其他形式

1

\[H_n = \binom{2n}{n} - \binom{2n}{n+1} \]

2

\[H_n = \frac{\binom{2n}{n}}{n+1} \]

3

\[H_n = \sum_{i=1}^{n} H_{i-1} H_{n-i} \]

特别地有 \(H_0 = H_1 = 1\)。

从网格问题证明：

枚举第一次到达 \(y=x\) 的点 \((i,i)\)，其中 \(1 \le i \le n\)。

那么前一半的方案数等价于 \((1,0)\) 到 \((i,i-1)\)，且不经过 \(y=x-1\) 的方案数，就是 \(H_{i-1}\)。

后一半是 \(H_{n-i}\)，那么由乘法原理一个 \(i\) 的贡献就是 \(H_{i-1} H_{n-i}\)。

4

\[H_n = \frac{H_n (4n-2) }{n+1} \]

经典问题

网格行走问题

从 \((0,0)\) 到 \((n,n)\) 且不经过 \(y=x\) 的方案数为 \(H_n\)。

从 \((0,0)\) 到 \((n,m)\) 且不经过 \(y=x\) 的方案数为 \(\binom{n+m}{n} - \binom{n+m}{m-1}\)。

如下图：

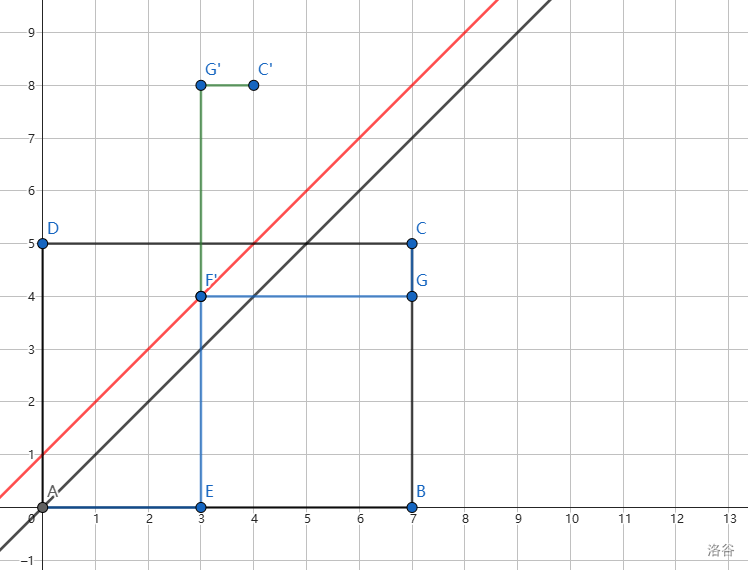
每一条不合法的路径都可以转化为一条 \((0,0)\) 到 \((m-1,n+1)\) 的路径

P1641 [SCOI2010] 生成字符串

加入一个 \(1\) 看成向右走，加入一个 \(0\) 看成向下走，就是上述问题。

出栈方案数问题

P1044 [NOIP 2003 普及组] 栈

将进栈看成向右，出栈看成向上即可。

二叉树总数

\(k\) 个节点可构造出二叉树总数是 \(H_k\)。

证明：枚举 \(i\)，左端点数 \(i-1\)，右端点数 \(n-i\)，成了两个子问题 \(H_{i-1},H_{n-i}\)，发现公式与卡特兰数是相同的。

阶梯划分问题

P2532 [AHOI2012] 树屋阶梯

考虑 \(f_i\) 表示 \(i\) 阶阶梯划分数量，考虑一个矩形 \((0,0)\) 划分到横坐标为 \(i\) 的点，剩下的就是 \(i-1\) 和 \(n-i\) 的子问题，正好符合卡特兰数的公式。