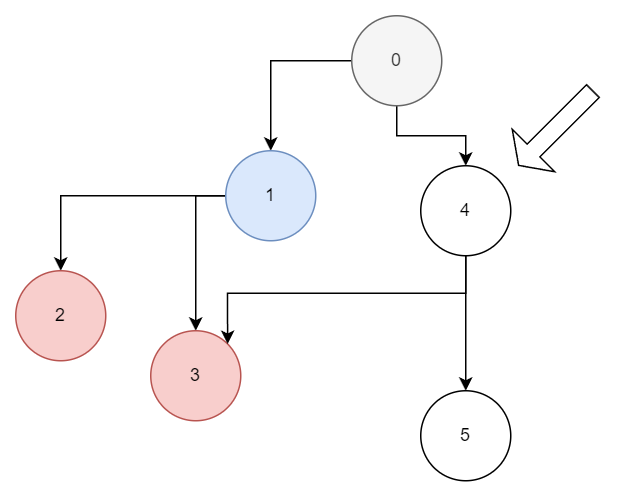
最短路径问题是图论中最经典且重要的应用问题之一。它的目标是找到一个图中从起点到终点的最短路径,即在所有可能的路径中,选择一条边权和最小的路径。该问题广泛存在于多个实际场景中,比如交通运输、通信网络、导航系统等。
在实际生活中,很多情况都涉及到寻找最短路径。例如,导航系统需要为用户推荐从当前位置到目的地的最短路线,或者在计算机网络中,数据包可能需要找到从源点到目标节点的最短传输路径。此外,物流公司在进行货物配送时,也会使用最短路径算法来最优化运输路线,减少成本和时间。
最短路径问题可以分为几类,主要区别在于图中边的权重特性。这里,我们关心的是“正权图”和“负权图”的区别:
-
正权图:在正权图中,所有边的权重都为正数。这类图广泛应用于实际生活中的路径规划问题,因为权重通常代表着距离、时间、费用等,通常都是正数。
-
负权图:与正权图不同,负权图允许边的权重为负数。负权边的存在可能导致问题变得复杂,因为如果某些路径经过负权边,可能会导致最短路径无限循环下降,无法收敛。因此,解决带有负权边的图时需要使用不同的算法,如 Bellman-Ford 算法。
在最短路问题上,正权图和负权图有着质的区别。本文将聚焦于正权图,并探讨 Dijkstra 算法在正权图中的应用。
Dijkstra 算法
Dijkstra 算法是一种典型的贪心算法,旨在解决单源最短路径问题。它的核心思想是每次选择当前距离起点最近的未访问节点,并逐步更新与其邻接的节点的最短路径。Dijkstra算法通过逐渐扩展已知的最短路径集合,最终得到从起点到所有节点的最短路径。
Dijkstra算法的执行步骤如下:
-
初始化:设定起点的距离为0,其他所有节点的距离为无穷大。将所有点划分为“已求解最短距离”和“未求解最短距离”两部分。开始起点的最短路径已知,其它节点的最短路径未知。
\[\text{dist}(s) = 0, \quad \text{dist}(v) = \infty \quad \text{for all other nodes } v \neq s \] -
选择当前最近节点:从未访问的节点中选择距离起点最近的节点,记为当前节点 \(u\)。
-
更新邻接节点的距离:对于当前节点 \(u\) 的所有邻接节点 \(v\),如果通过 \(u\) 到 \(v\) 的路径比已知的最短路径更短,则更新 \(v\) 的最短路径:
\[\text{dist}(v) = \min(\text{dist}(v), \text{dist}(u) + w(u, v)) \]其中 \(w(u, v)\) 表示边 \(u \to v\) 的权重。
-
标记当前节点已访问:将当前节点 \(u\) 标记为已访问,不再参与后续的最短路径计算。
-
重复上述过程:重复步骤 2 到步骤 4,直到所有节点都被访问过,或者起点到所有其他节点的最短路径已经找到。
Dijkstra 算法的正确性
Dijkstra 算法的正确性可以通过“贪心选择性质”和“最短路径定理”来证明。
-
贪心选择性质:对于任何一个顶点 \(v\),如果已知通过某个节点 \(u\) 到 \(v\) 的路径是当前最短的路径,那么从起点到 \(v\) 的最短路径一定是通过 \(u\) 到 \(v\) 的路径。也就是说,Dijkstra算法每次选择距离起点最近的未访问顶点 \(u\),这个选择是局部最优的,从而保证了全局最优。
-
最短路径定理:如果一个路径是从源点到目标节点的最短路径,那么在路径的任意前缀段(从起点到某个中间节点的路径)也是最短路径。这个定理保证了算法每次扩展的路径是最短的。
基于这些性质,Dijkstra算法能够在每次迭代中得到当前节点的最短路径,最终保证算法得到从源点到所有节点的最短路径。
在正权图中,每一次选择当前最短节点的操作是有效的,那是因为每个新选择的节点都不会影响已确定最短路径的正确性。但在负权图中,负权边可能导致我们先前认为最短的路径变得不再最短。因此,如果图中包含负权边,Dijkstra 算法无法正确地更新路径,也就无法确保最终结果是全局最优的。
// 二叉堆版本
vector<long long> dijkstra(int s) {vector<long long> dist(n, LLONG_MAX / 2);vector<bool> visited(n, false);dist[s] = 0;priority_queue<pair<long long, int>, vector<pair<long long, int>>, greater<pair<long long, int>>> pq;pq.push({0, s});while (!pq.empty()) {int u = pq.top().second;pq.pop();if (visited[u]) continue;visited[u] = true;for (const auto &e : adj[u]) {int v = e.to;int w = e.weight;if (dist[v] > dist[u] + w) {dist[v] = dist[u] + w;pq.push({dist[v], v});}}} return dist;
}
时间复杂度分析
Dijkstra 算法的时间复杂度依赖于其实现方式,主要影响因素是如何选择距离起点最近的未访问节点。我们将分析不同的数据结构实现下的时间复杂度。
-
暴力方法(无堆实现):
在暴力方法中,我们每次从未访问的节点中选择距离起点最近的节点,通常通过遍历所有未访问节点来实现。这种方法的时间复杂度为 \(O(V^2)\),其中 \(V\) 是图中节点的数量。每次选择最短路径节点需要 \(O(V)\) 时间,更新邻接节点的距离需要 \(O(E)\) 时间(\(E\) 为边数),总的时间复杂度为 \(O(V^2)\)。
-
使用二叉堆优化:
通过使用二叉堆(最小堆)来维护未访问节点的最短距离,我们可以在每次选择最短路径节点时做到 \(O(\log V)\) 时间复杂度。对于每条边的更新操作,也需要 \(O(\log V)\) 时间。因此,使用二叉堆后,Dijkstra算法的时间复杂度为 \(O((V + E) \log V)\)。
-
使用 k 叉堆优化:
使用 \(k\) 叉堆时,每次选择最短路径节点的时间复杂度为 \(O(\log_k V)\),而每条边的更新操作仍然是 \(O(\log_k V)\)。对于一般情况,\(k\) 的取值在实践中可能比二叉堆略大,对于非常稠密的图,多叉堆比二叉堆更好。总体时间复杂度为 \(O((V + E) \log_k V)\)。
-
使用斐波那契堆优化:
斐波那契堆是一个更高级的堆结构,更新操作(减小堆中元素的值)的摊销时间复杂度为 \(O(1)\)。因此,使用斐波那契堆的时间复杂度为 \(O(E + V \log V)\),这是理论的最优实现。
总结来说,Dijkstra算法的时间复杂度在不同的数据结构下有显著的差异,具体选择哪种结构取决于图的特性和实际需求。
Dijkstra 算法是正权图的最佳选择
Dijkstra 算法在正权图中有着显著的优势,适用于有向图,也适用于无向图。稳定且效率高。但其无法处理负权图。Bellman-Ford 算法才能够处理负权边并检测负权环。
对于全源最短路径, Floyd-Warshall 算法是一个用于求解所有顶点对之间最短路径的算法,其时间复杂度为 \(O(V^3)\)。虽然该算法适用于所有类型的图,但对于大规模图,尤其是图中边数较少时,Floyd-Warshall 算法的计算成本远高于 Dijkstra 算法。Dijkstra 算法更加高效,我们可以直接分别以每个点作为源点运行一次算法,得到全源最短路径。
A* 算法是对 Dijkstra 算法的一种优化,通常用于有启发式信息的路径搜索问题。A* 算法通过加入启发式函数来引导搜索,使得算法在求解最短路径时更加高效,尤其在路径搜索中与目标节点的距离较近时。若非单纯的图论求解,而在某些存在启发式的场景下(如现实地图,坐标系中的点等),可以在 dijkstra 中引入启发式。
当边权均为 1 时,我们发现 dijstra 退化为 BFS,不再需要优先队列了。反过来说,dijstra 就是 BFS 在边权不等需要用优先队列先取出最小值的扩展。