题目1
代码
#include<bits/stdc++.h>
using namespace std;const int MAX = 2e+5;
int ary[MAX],prefix[MAX]; int main()
{int n; cin>>n;for(int i=1;i<=n;i++){cin>>ary[i];prefix[i] = prefix[i-1] + ary[i];}int minGap = 0x7fffffff, maxSum = 0x80000000;for(int i=1;i<=n;i++) {minGap = min(minGap,prefix[i-1]);maxSum = max(maxSum, prefix[i]-minGap);}cout<<maxSum<<endl; return 0;
}解题思路
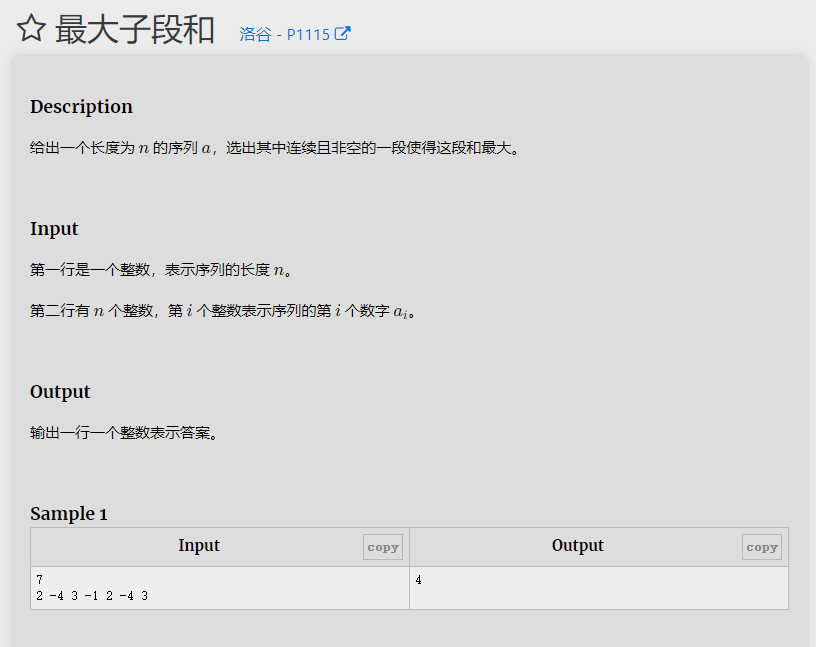
最大子序列和问题:
输入一个整数序列,要求找到一个子序列,使得该子序列的元素之和最大。
使用动态规划的思想,构建一个前缀和数组 prefix,其中 prefix[i] 表示前 i 个元素的和。
遍历前缀和数组,对于每个位置 i,找到 i 之前的最小前缀和 minGap,然后计算以 i 为结尾的子序列的最大和 prefix[i] - minGap。
最终答案即为所有 prefix[i] - minGap 中的最大值。
题目2
代码
#include<iostream>
using namespace std;
int main()
{int n,m,w,v;int f[1000000005];cin>>m>>n;for(int i=1; i<=n; i++){cin>>w>>v;for(int j=m; j>=w; j--){f[j] = max(f[j],f[j-w]+v);}}cout<<f[m];return 0;
}
解题思路
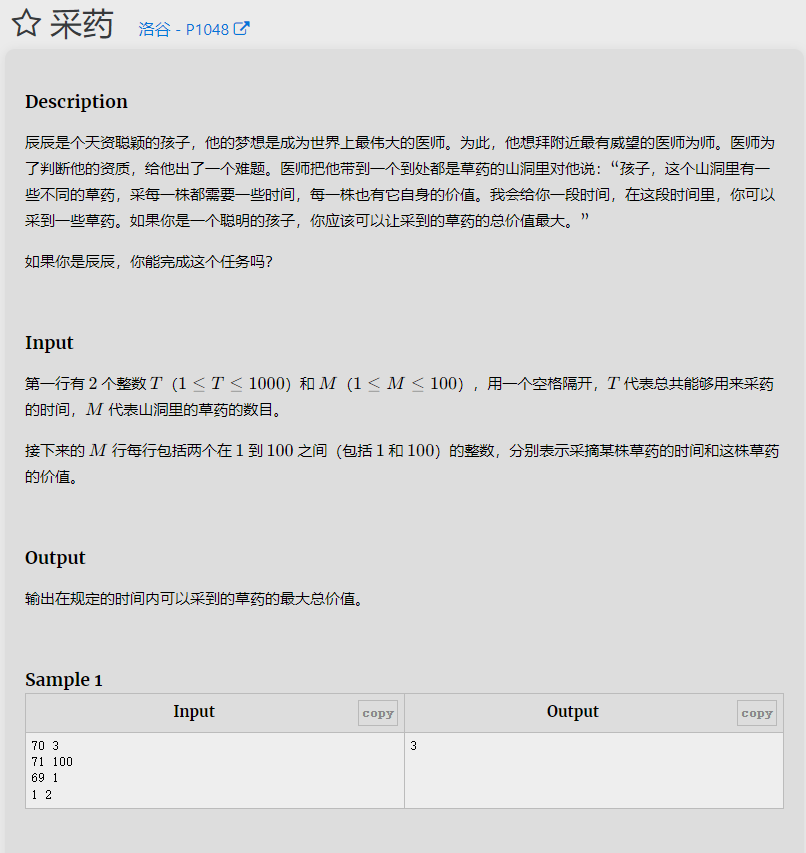
背包问题:
输入背包的容量 m 和物品的数量 n,以及每个物品的价值 v 和重量 w。
使用动态规划的思想,构建一个二维数组 f,其中 f[i][j] 表示在前 i 个物品中选择,且背包容量为 j 时的最大价值。
状态转移方程为 f[i][j] = max(f[i-1][j], f[i-1][j-w[i]] + v[i]),即不选择当前物品或选择当前物品,取两者中的最大值。
最终答案即为 f[n][m],表示在所有物品中选择,且背包容量为 m 时的最大价值。
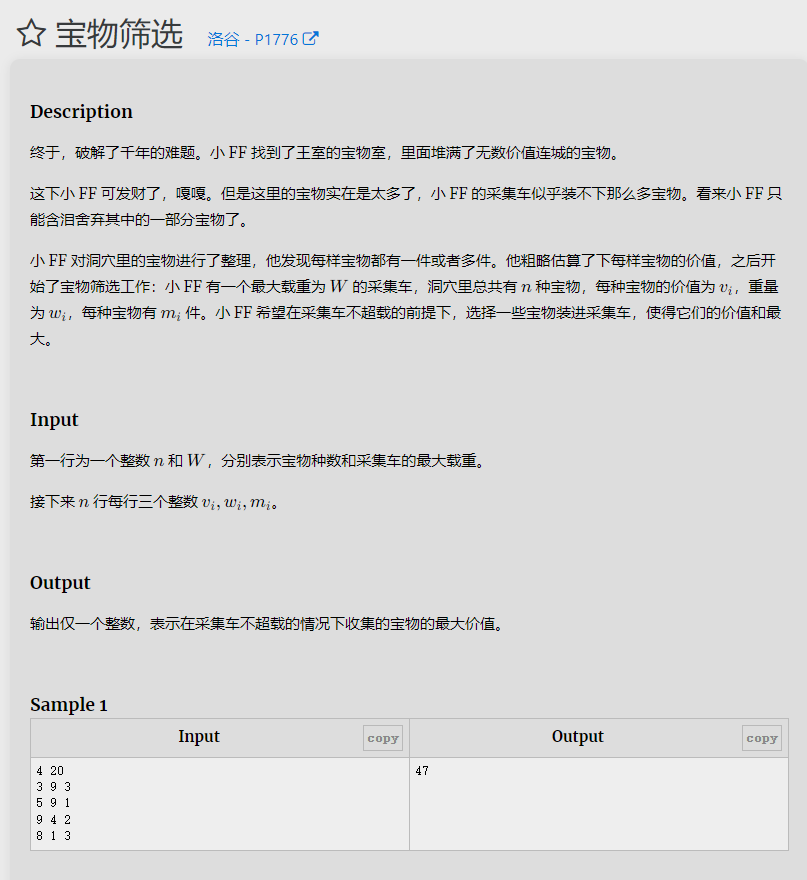
题目3
代码
#include <bits/stdc++.h>
using namespace std;
#define max_Heap(x) priority_queue<x, vector<x>, less<x>>
#define min_Heap(x) priority_queue<x, vector<x>, greater<x>>
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> PII;
typedef pair<long long, long long> PLL;
const double PI = acos(-1);int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int n, m;cin >> n >> m;vector<ll> dp(m + 1, 0);// 价值,重量,个数ll value, weight, cnt;for (int i = 0; i < n; i++){cin >> value >> weight >> cnt;vector<ll> tmp;// 二进制分解for (ll j = 1; j <= cnt; j <<= 1){tmp.push_back(j);cnt -= j;}if (cnt != 0)tmp.push_back(cnt);// 转换成01背包dpfor (int k = 0; k < tmp.size(); k++){for (int j = m; j >= 0; j--){// 更新价值和重量ll a = value * tmp[k];ll b = weight * tmp[k];if (j >= b){dp[j] = max(dp[j], dp[j - b] + a);}}}}cout << dp[m];return 0;
}
解题思路
完全背包问题:
输入背包的容量 m 和物品的数量 n,以及每个物品的价值 v、重量 w 和数量 cnt。
使用动态规划的思想,构建一个一维数组 dp,其中 dp[j] 表示背包容量为 j 时的最大价值。
对于每个物品,进行二进制分解,将其拆分成若干个数量为 2 的幂的物品,然后按照 01 背包的方式进行处理。
最终答案即为 dp[m],表示在所有物品中选择,且背包容量为 m 时的最大价值。
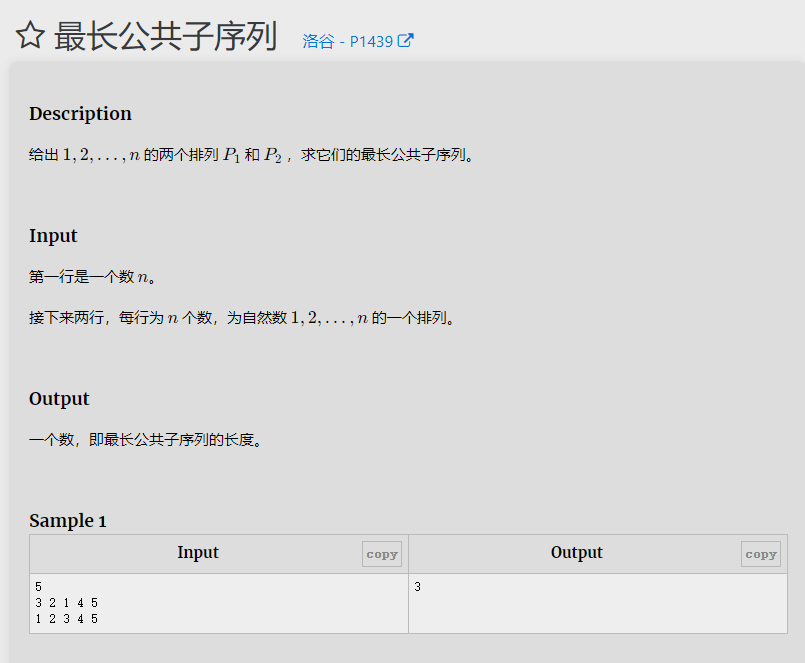
题目4
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;int a[N];
int b[N];
int pos[N];
int d[N];
int n;int main()
{cin >> n;for (int i = 1; i <= n; i++){scanf ("%d", &a[i]);pos[a[i]] = i;}for (int i = 1; i <= n; i++){scanf ("%d", &b[i]);}int len = 0;for (int i = 1; i <= n; i++){int now = pos[b[i]];if (now > d[len]){d[++len] = now;}else{int t = lower_bound(d + 1, d + len + 1, now) - d;d[t] = now; }}cout << len << endl;return 0;
}
解题思路
最长上升子序列问题:
输入一个整数序列,要求找到一个最长的子序列,使得该子序列中的元素严格递增。
使用动态规划的思想,构建一个一维数组 d,其中 d[i] 表示以第 i 个元素结尾的最长上升子序列的长度。
遍历输入序列,对于每个元素 b[i],在 d 数组中找到第一个大于等于 b[i] 的位置 j,并更新 d[j] 为 d[j-1] + 1。
最终答案即为 d 数组中的最大值。
题目5

代码
#include<bits/stdc++.h>
using namespace std;
const long long mo=998244353;
long long t,n;
void solve(){cin>>n;vector<long long>a(n+1),f1(n+1),f2(n+1);for(int i=1;i<=n;i++){cin>>a[i];}if(a[1]==0){f1[1]=1;f2[1]=1;}else{f1[1]=0;f2[1]=1;}for(int i=2;i<=n;i++){f2[i]=f1[i-1];if(a[i]==a[i-1]){f1[i]=(f1[i]+f1[i-1])%mo;}if(a[i]==a[i-2]+1){f1[i]=(f1[i]+f2[i-1])%mo;}}cout<<(f1[n]+f2[n])%mo<<"\n";return;
}
int main(){cin>>t;while(t--){solve();}return 0;
}
解题思路
动态规划解决序列问题:
输入一个整数 n,表示序列的长度,然后输入一个整数序列 a。
定义两个状态数组 f1 和 f2,分别表示以第 i 个元素结尾的满足条件的子序列的个数,其中 f1 表示第 i 个元素与前一个元素不同的情况,f2 表示第 i 个元素与前一个元素相同的情况。
初始化 f1[1] 和 f2[1] 的值,根据题目条件进行初始化。
遍历序列,根据当前元素与前一个元素的关系,更新 f1 和 f2 的值。
最终答案为 f1[n] + f2[n],表示以第 n 个元素结尾的满足条件的子序列的总个数。
题目6

代码
#include<bits/stdc++.h>
using namespace std;
const int N=5002;
int cnt[N],dp[N],v[N],n,t,x;
int main(){ios_base::sync_with_stdio(false);cin.tie(0); cout.tie(0);cin>>t;for(int i=1;i<=t;i++){cin>>n;for(int j=1;j<=n;j++){cin>>x;cnt[x]++;}int len=0;for(int j=1;j<=5000;j++) if(cnt[j]) len++,v[len-1]=cnt[j];for(int k=1;k<len;k++){for(int j=k;j>=v[k];j--){dp[j+1]=max(dp[j-v[k]]+1,dp[j+1]);}}int maxx=0;for(int j=1;j<=len;j++) maxx=max(maxx,dp[j]);cout<<len-maxx<<endl;memset(cnt,0,sizeof(cnt));memset(dp,0,sizeof(dp));memset(v,0,sizeof(v));}return 0;
}
解题思路
动态规划解决分组问题:
输入一个整数 t,表示测试用例的数量。
对于每个测试用例,输入一个整数 n,表示物品的数量,然后输入 n 个整数,表示每个物品的价值。
定义一个状态数组 dp,其中 dp[i] 表示前 i 个物品中,能够组成的最大价值。
初始化 dp 数组,对于每个物品,遍历所有可能的分组情况,更新 dp 数组的值。
最终答案为 dp[n],表示前 n 个物品中能够组成的最大价值。