莫队算法学习笔记

莫队算法的发明者是一个叫做 莫涛 的人，所以被称为莫队算法，简称莫队。

英语 Mo's algorithm。

使用场景

莫队算法常常被用来处理多次区间询问的问题，离线处理询问（必须满足！！！）。

插叙：离线是一种得到所有询问再进行计算的方法，是很重要的思想。

对于这种“区间询问”的问题，我们现在就已经可以使用好几种方法：甚至还可以维护修改的线段树、树状数组（不过使用场景有限），以及同样可以很快解决问题的 ST 表……

所以，莫队在很多时候可以被其他算法代替。但是莫队也有很多“专利”，就像分块可以解决很多线段树解决不了的问题（虽然就是慢了点）。

树状数组需要可以区间减法，线段树和 ST 表需要可以区间合并，而莫队需要可以进行区间扩张和区间缩短。

题外话：区间扩张和区间缩短你能想到什么？没错，尺取法。

算法思路

我们不妨解决一个问题，从问题中了解算法的大体思路。

问题：询问区间和。（这显然可以使用前缀和进行维护，但是我们假装不会这个）

法一：纯暴力。枚举区间内所有的数，加起来即可。 时间复杂度 \(O(qn)\)。

不再阐述。

法二：另一种暴力。方法如下。

假设我们现在已经计算出了 \([l_1,r_1]\) 的区间和，而现在又需要计算 \([l_2,r_2]\) 的区间和。

出于懒的本性，我们考虑在原 \([l_1,r_1]\) 的区间和上动一些手脚。

直接将 \(l_1\) 移到 \(l_2\)，然后将 \(r_1\) 移到 \(r_2\)，顺便维护一下即可。

复杂度仍然是 \(O(qn)\)，好像没有优化多少。

好像比上面的方法还要蠢，但是不必灰心，这种“蠢”的方法正是莫队的起源。

法三：莫队。对询问进行了顺序调整，然后使用法二的方法处理即可。

先对询问的序列按照左边界的值分成了 \(\sqrt(n)\) 个块长为 \(\sqrt(n)\) 的块（好奇怪）。

然后对询问排序：

• 第一关键字：按左边界的块号从小到大排序。（啊？）

• 第二关键字：按右边界从小到大排序。

---

看起来非常古怪的一个排序，那么这个排序有什么奇效呢？我们来举个例子。

设 \(n=9,q=10\)。

我们有如下查询：\([2,5],[4,5],[5,9],[1,6],[2,3],[7,8],[9,9],[6,7],[2,8],[3,4]\)。

而我们按照块号排序之后变成了 \([2,3],[3,4],[2,5],[1,6],[2,8],[4,6],[6,7],[5,9],[7,8],[9,9]\) 这个样子。

然后我们画一个图，来使用平面直角坐标系来绘出这些区间（左端点变成了横坐标，右端点变成了纵坐标）。

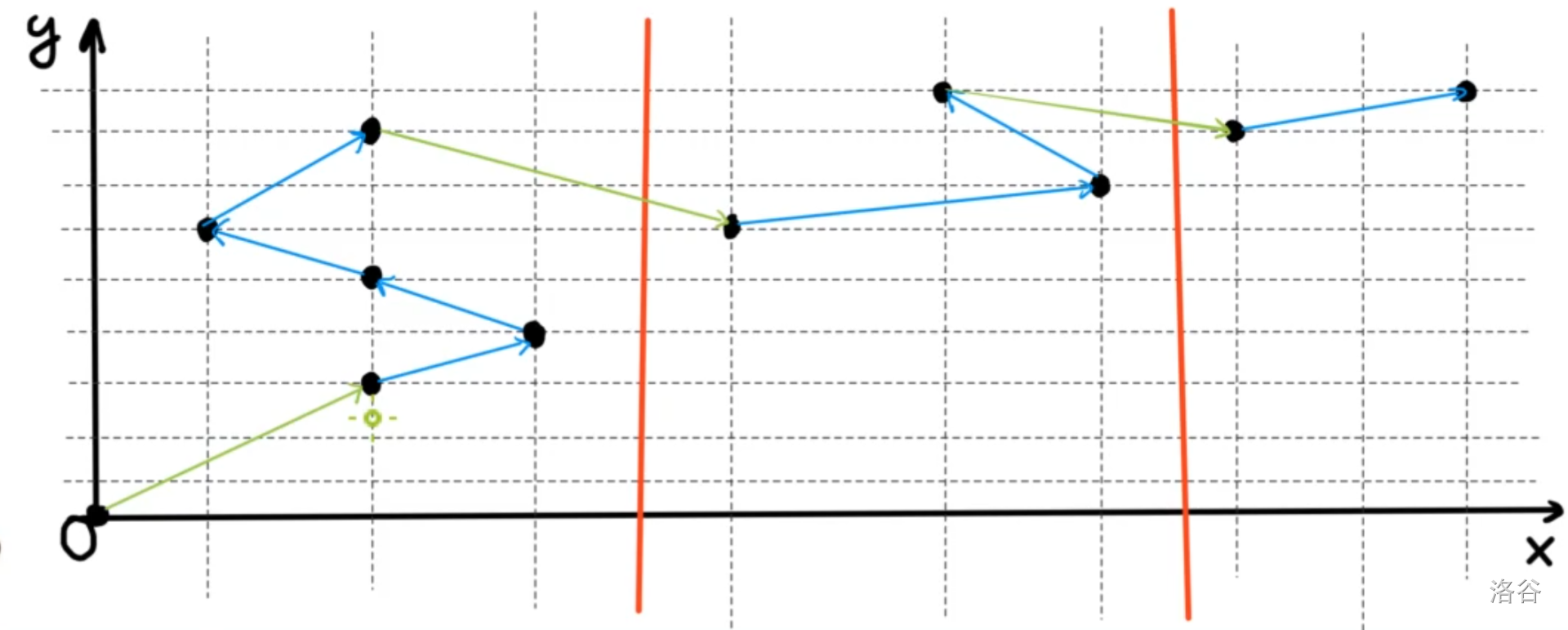
解释一下图片的含义：

为了便于描述，我们先设一开始的区间在 \([0,0]\) 的位置。

因为第一关键字使用块号来排序，所以同一个块内的点一定在一起，已经使用粗的红线分割出三个块（\(\sqrt(9)=3\)）。

我们使用蓝色边来体现块内结点移动，然后使用橙色边来体现块间结点的移动。

容易知道，块的数量是 \(O(\sqrt(n))\) 个，而块的横坐标长度是 \(\sqrt(n)\)（注意，这里的每一个点的横纵坐标均不可能超过 \(n\)，这可是查询）。

因为橙色边的数量和块的数量有关，所以橙色边的数量最多是 \(O(\sqrt(n))\)个，而每一次点之间移动的复杂度不超过 \(n\)（这是区间移动，左端点和右端点总共最多移动 \(n\) 下）。

因此，单算橙色边，时间复杂度为 \(O(n \sqrt(n))\)。

---

橙色边分析的落脚点在于原区间的移动，考虑使用 抽象之后的点之间的移动 来分析蓝色边的复杂度。

显然，点之间的移动 的次数取决于两点之间的纵坐标和横坐标差。

考虑纵坐标。因为第一关键字在块内中已经失去了作用，而第二关键字保证了我们在块内一定是越爬越高。

而每一个点的横纵坐标均不可能超过 \(n\)，所以单个块内纵坐标总共也只会对时间造成 \(n\) 的影响。

所有的块的纵坐标影响合起来，也只有 \(O(n \sqrt(n))\)，可以接受。

考虑横坐标。根据前文，每一个块的横向长度都不可能超过 \(\sqrt(n)\)，所以横坐标的块内单次只会造成 \(\sqrt(n)\) 的时间影响。

而总共有 \(q\) 个点，相乘起来，是 \(O(q \sqrt(n))\)，仍然可以接受。

---

经过上面的分析，你现在知道为什么这样排序了吧！

实际上，所有的看起来古怪的算法，都是为了以后恰到好处的运用。

综上所述，莫队的时间复杂度为 \(O((q+n) \sqrt(n))\)。排序是 \(O(n\log n)\) 的，但是相比 \(\sqrt(n)\) 来说还是可以忽略的。

这就是莫队的想法。