离散化学习笔记
OP:又是一如既往的周更。。。水死了
定义
- 离散化:将数字映射为是第几小的数,其保证数据在Hash之后仍然保持原来的全/偏序关系,能够解决:通过元素相对大小即可解决的问题。
- 其实本质上就是哈希的一种特殊规则而已。(离散化简化了不止亿点)
目标
- 将一堆乱序且不保证全部相邻的数组变成紧凑且在这些数之间的每个数都被充分利用。
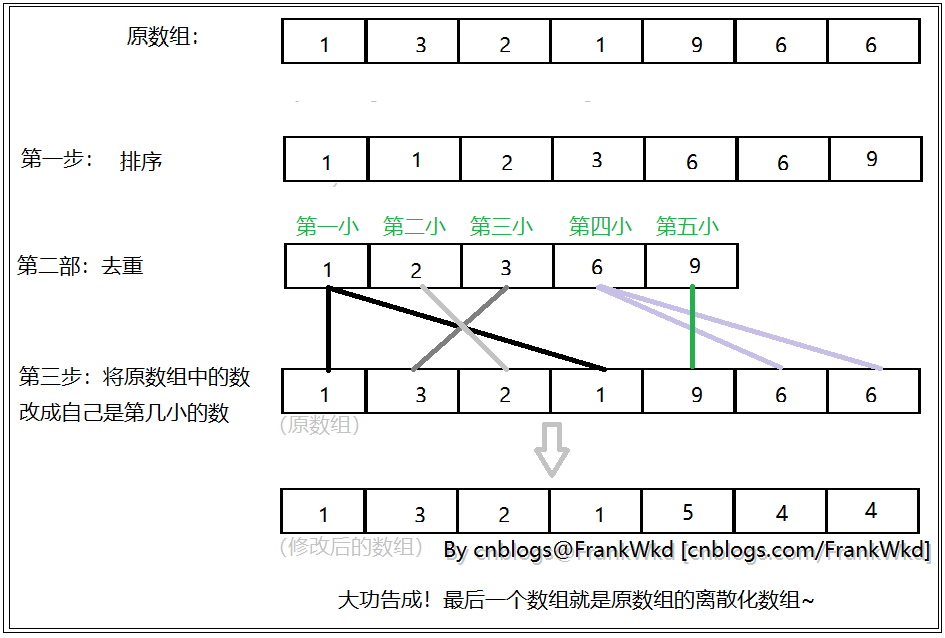
- 说人话:将每个数改为自己是第几小的数。(我语文太差,具体请看例子:)
步骤
- 1.数组中存在重复的元素,因此需要排序&去重;
- 2.计算每个 \(a_i\) 是第几小的数。【二分查找】
代码:
点击查看代码
图源`v.czos.cn`,侵删。

习题
又到了令人欢快的做题时间
本课习题:共9道题,2道难题。来源:oj.czos.cn。
01 统计数字
点击查看题面内容
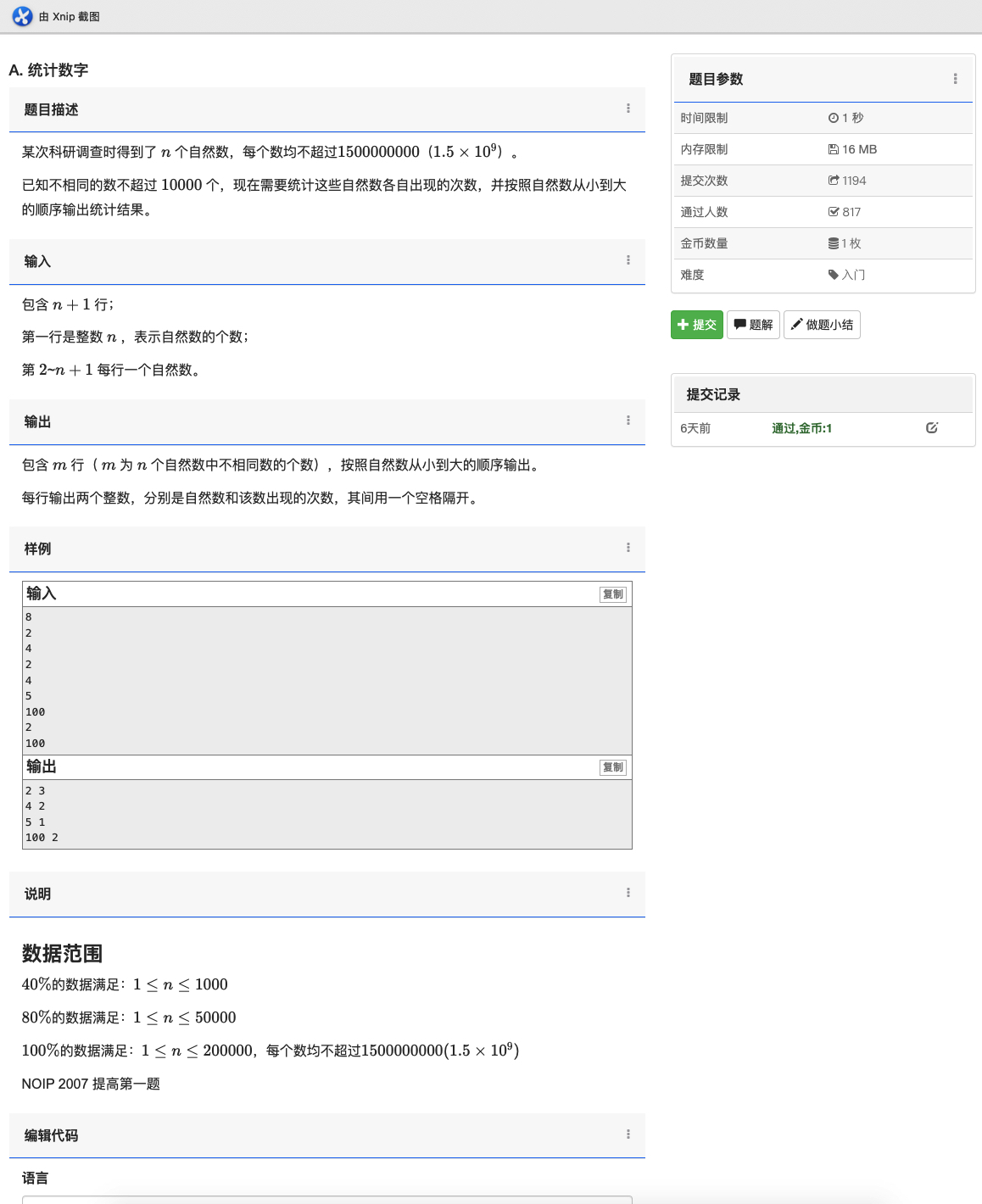
解法:其实就是简单的离散化,因为 \(n\) 比较大,所以我们考虑使用桶排序来统计这些数的出现次数。即: \(ans_i\) 表示 数值为 \(i\) 的数的出现次数。因为数组最大开 \(10^7\) (保守估计),且 \(n\) 明显小于 \(A_i\) 的数据范围,所以肯定在这中会有出现次数为 \(0\) 的数。所以我们先把数组离散化,然后桶排序直接输出即可。
点击查看代码
//提示:此代码遵守GNU GPL 2.0开源协议。
//作者:FrankWkd
//博客:https://cnblogs.com/FrankWkd
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
const int M = 1e4 + 10;
int a[N], b[N], c[M];
int n, k;
int main() {cin >> n;for (int i = 1; i <= n; i++) {cin >> a[i];b[i] = a[i];}sort(b + 1, b + 1 + n);k = unique(b + 1, b + 1 + n) - b - 1;for (int i = 1; i <= k; i++) {a[i] = lower_bound(b + 1, b + 1 + k, a[i]) - b;c[a[i]]++;}for (int i = 1; i <= k; i++) {cout << b[i] << " " << c[i] << endl;}return 0;
}
02 供水点
点击查看题面内容
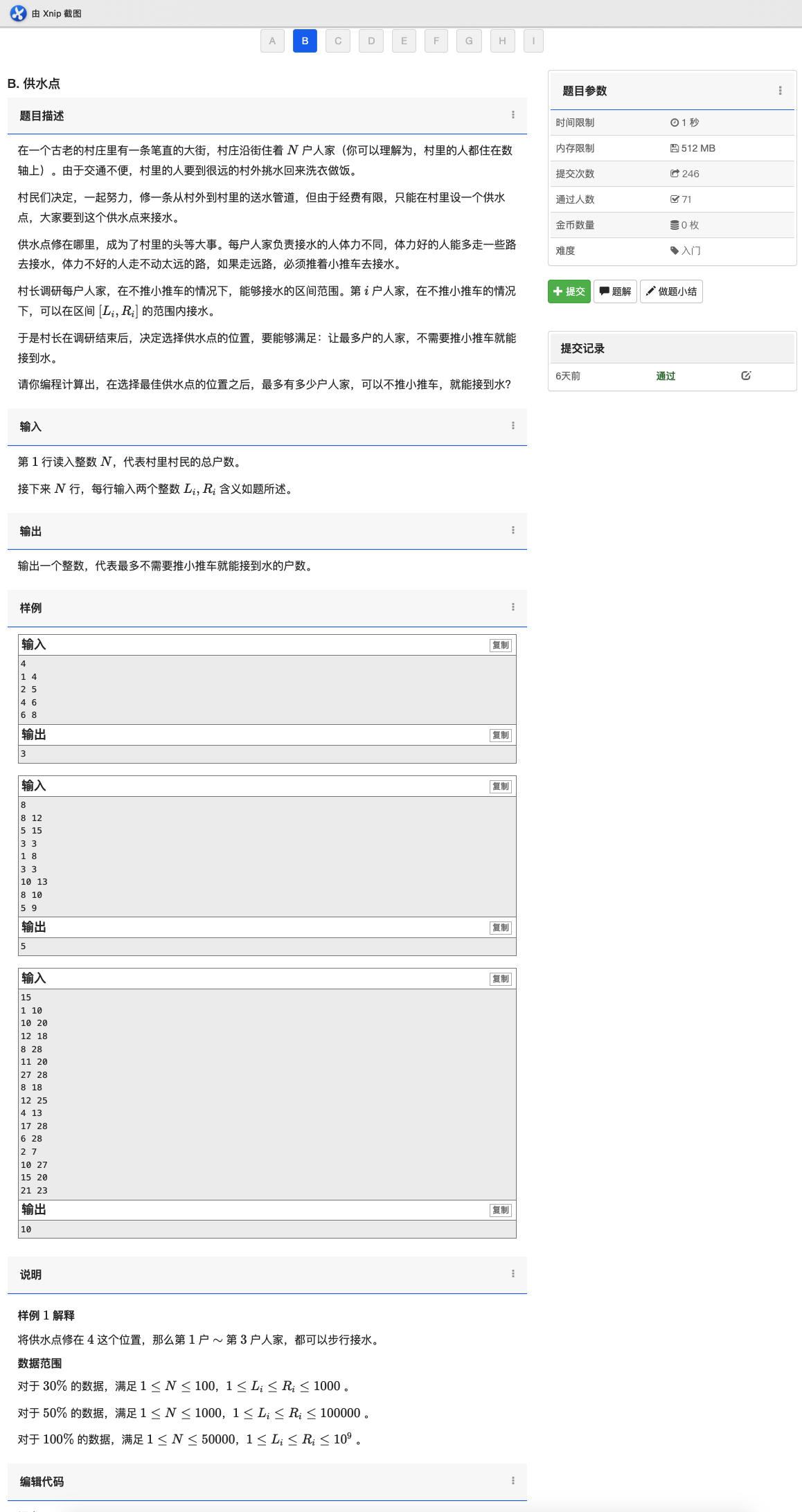
解法:定义 \(ans\) 数组,存储每个位置可以不推车来的人数,遇到一个 \([L,R]\)就将 \(ans\) 对应的区间加一,这个过程可以用差分来完成。最后 \(ans\) 数组里面最大的值就是结果。\([L,R]\) 太大需要离散化。
点击查看代码
//提示:此代码遵守GNU GPL 2.0开源协议。
//作者:FrankWkd
//博客:https://cnblogs.com/FrankWkd
#include <bits/stdc++.h>
using namespace std;int a[200010];
int b[200010];
int ans[400010];
int all[400010];int main() {int n;cin >> n;int k = 0;for (int i = 1; i <= n; i++) {cin >> a[i] >> b[i];all[++k] = a[i];all[++k] = b[i];}sort(all + 1, all + 1 + k);k = unique(all + 1, all + k + 1) - all - 1;for (int i = 1; i <= n; i++) {a[i] = lower_bound(all + 1, all + 1 + k, a[i]) - all;b[i] = lower_bound(all + 1, all + 1 + k, b[i]) - all;ans[a[i]]++, ans[b[i] + 1]--;}int maxx = 0;for (int i = 1; i <= k; i++) {ans[i] += ans[i - 1];maxx = max(maxx, ans[i]);}cout << maxx << endl;
}
03 自动灌溉
点击查看题面内容
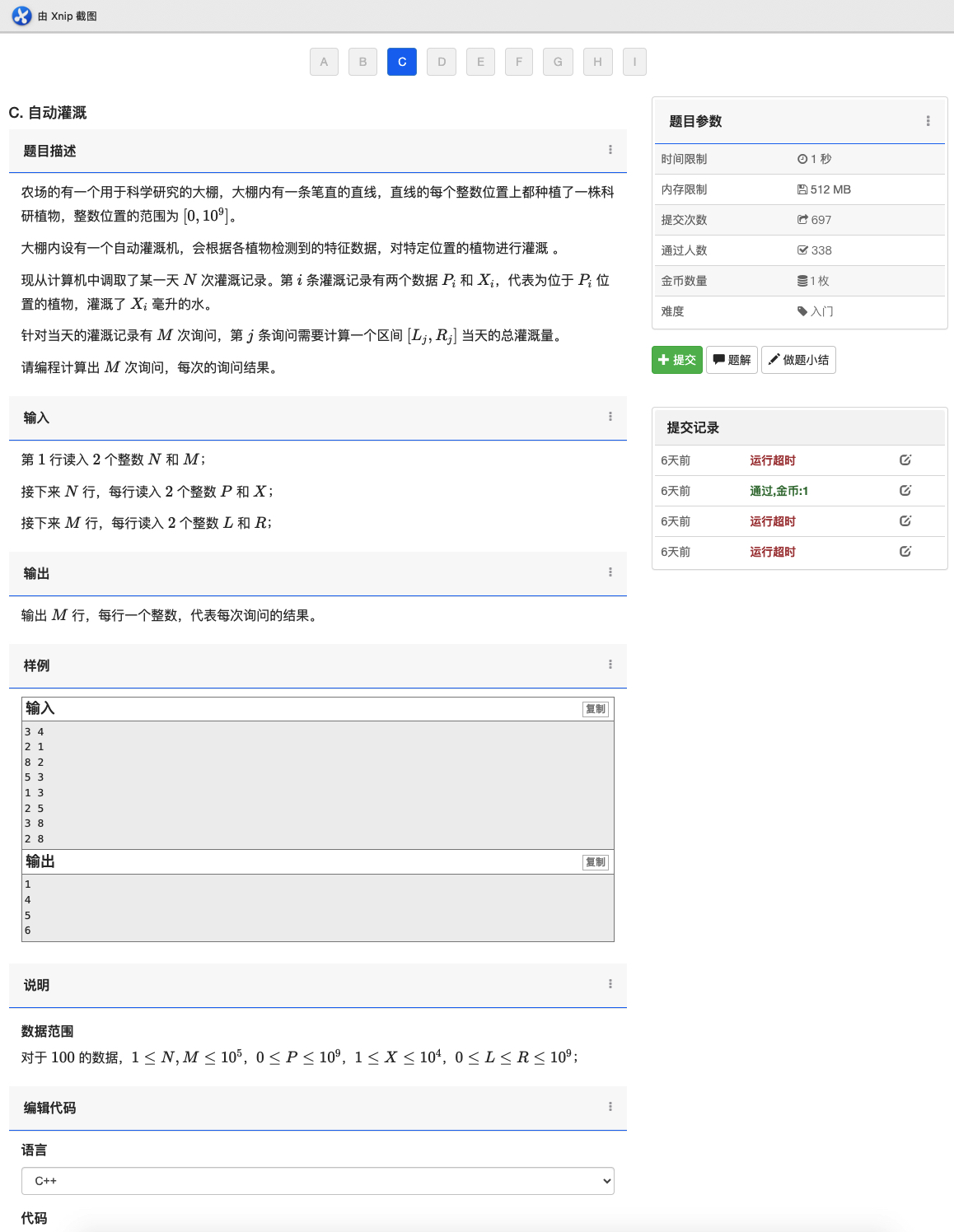
解法:跟T2差不多,都要离散化 \([L,R]\) ,只是询问略有不同,求区间和用什么?前缀和啊
点击查看代码
//提示:此代码遵守GNU GPL 2.0开源协议。
//作者:FrankWkd
//博客:https://cnblogs.com/FrankWkd
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include <bits/stdc++.h>
using namespace std;
int ans[1010100];
int n, m, k;
int p[100010], x[100010];
int l[100010], r[100010];
int all[600010];
int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin >> n >> m;for (int i = 1; i <= n; i++) {cin >> p[i] >> x[i];all[++k] = p[i];}for (int i = 1; i <= m; i++) {cin >> l[i] >> r[i];all[++k] = l[i];all[++k] = r[i];}sort(all + 1, all + 1 + k);k = unique(all + 1, all + 1 + k) - all - 1;for (int i = 1; i <= n; i++) {p[i] = lower_bound(all + 1, all + 1 + k, p[i]) - all;ans[p[i]] += x[i];}for (int i = 1; i <= m; i++) {l[i] = lower_bound(all + 1, all + k + 1, l[i]) - all;r[i] = lower_bound(all + 1, all + k + 1, r[i]) - all;}for (int i = 1; i <= k; i++) {ans[i] += ans[i - 1];}for (int i = 1; i <= m; i++) {cout << ans[r[i]] - ans[l[i] - 1] << endl;}
}
04 饲养母鸡
点击查看题面内容
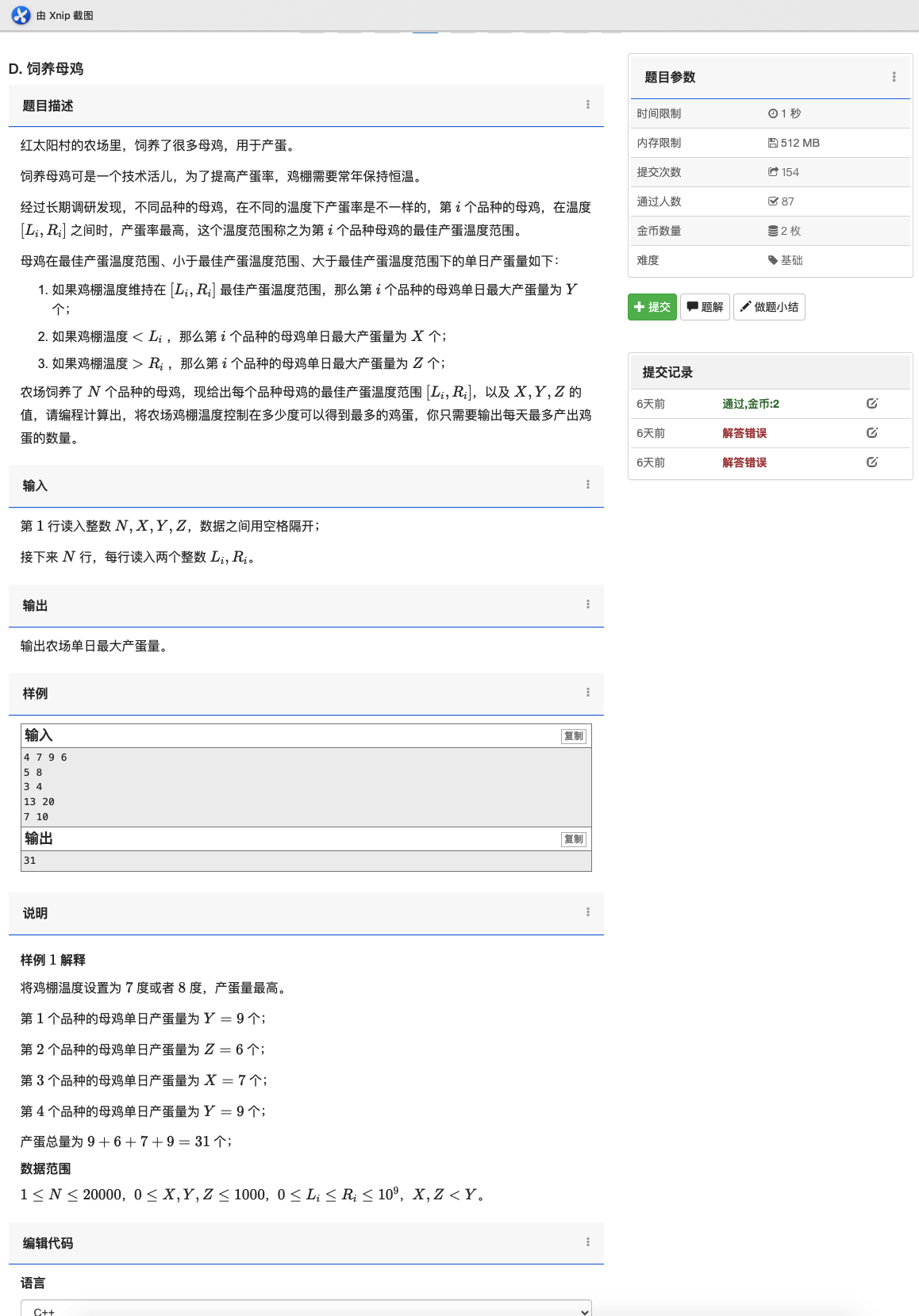
解法:跟T2差不多,问的问题是一样的,但是新加入了两条规则。那我们对于每个 \([L,R]\) ,将 \(ans\) 数组中的区间 \([0,L-1]\) 加上 \(X\) (前缀和),再将 \([L,R]\) 加上 \(Y\) ,最后将 \([R+1,最后]\) 加上 \(Z\)。直接前缀和完成。那最后是哪里呢?因为从 \(R+1\) 一直到最后都要加上 \(Z\),那直接将 \(ans_{r+1}\) 加上 \(Z\),然后就能够一直加到最后了。输出 \(ans\) 数组的最大值即可。
点击查看代码
//提示:此代码遵守GNU GPL 2.0开源协议。
//作者:FrankWkd
//博客:https://cnblogs.com/FrankWkd
#include <bits/stdc++.h>
using namespace std;int l[20010], r[20010];
int n, x, y, z;
int all[100100];
int k;
int ans[100100];
int main() {cin >> n >> x >> y >> z;for (int i = 1; i <= n; i++) {cin >> l[i] >> r[i];all[++k] = l[i], all[++k] = r[i];}sort(all + 1, all + 1 + k);k = unique(all + 1, all + 1 + k) - all - 1;for (int i = 1; i <= n; i++) {l[i] = lower_bound(all + 1, all + 1 + k, l[i]) - all;r[i] = lower_bound(all + 1, all + 1 + k, r[i]) - all;ans[1] += x, ans[l[i]] -= x;ans[l[i]] += y, ans[r[i] + 1] -= y;ans[r[i] + 1] += z;}int maxx = 0;for (int i = 1; i <= k; i++) {ans[i] += ans[i - 1];maxx = max(maxx, ans[i]);}cout << maxx << endl;
}
05
点击查看题面内容
解法:
点击查看代码
//提示:此代码遵守GNU GPL 2.0开源协议。
//作者:FrankWkd
//博客:https://cnblogs.com/FrankWkd