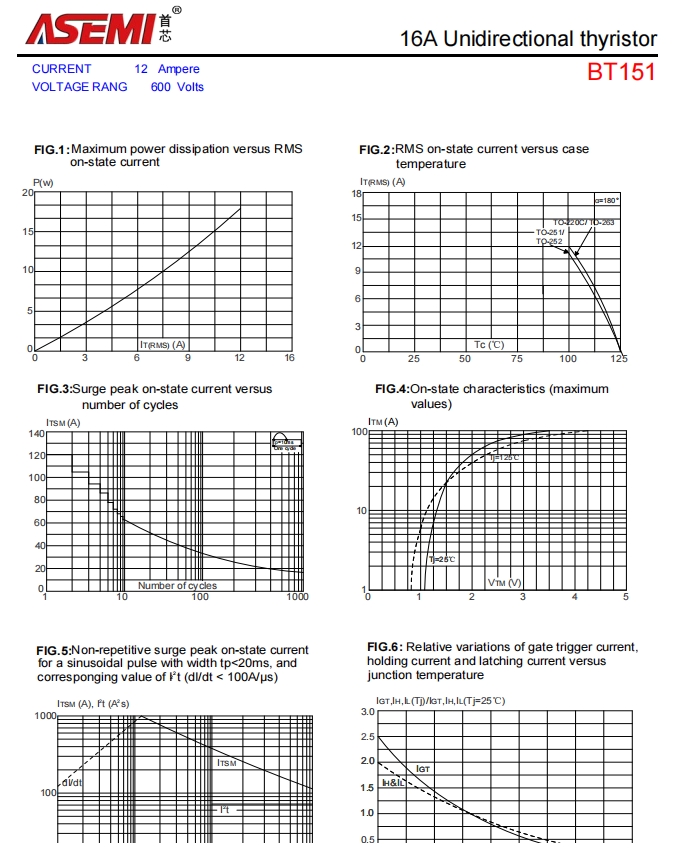
我们考虑阶乘 \(n!\) 的素因数分解 \(n! = p_1^{a_1} p_2^{a_2} \cdots p_k^{a_k}\),由于阶乘 \(n!\) 的因数位于 \([1,n]\) 区间内,因此阶乘 \(n!\) 的各个素因数 \(p_i \in [1,n]\)。我们用 \(\varepsilon_{p_i}(n!)\) 表示阶乘 \(n!\) 的素因数 \(p_i\) 的幂次。
参考素因数 \(p_i\) 及其幂次对表示阶乘 \(n!\) 的贡献,我们以素数 \(2\) 与阶乘 \(10!\) 为例,因子 \(2=2^1,4=2^2,8=2^3\) 分别贡献了素数 \(2\) 的 \(1,2,3\) 个幂次,因此对于一般的阶乘 \(n!\) 我们可以给出计算公式 \(\varepsilon_2(n!) = \lfloor\frac{n}{2}\rfloor + \lfloor\frac{n}{4}\rfloor + \lfloor\frac{n}{8}\rfloor + \cdots = \sum_{k \geq 1} \lfloor\frac{n}{2^k}\rfloor\)。这个和式是有限的,因为 \(2^k > n\) 时求和项为零,只有 \(\lfloor \log n \rfloor\) 个非零项。将我们的发现推广到任意的素数 \(p\) ,根据与前面同样的推理,我们就有
我们从求和项中直接去掉底,然后对无穷几何级数求和,我们得到一个上界:


![[QOJ 8366] 火车旅行](https://img2024.cnblogs.com/blog/3584318/202502/3584318-20250224140737540-1060414145.png)

![BUUCTF-RE-[2019红帽杯]easyRE](https://img2024.cnblogs.com/blog/3596699/202502/3596699-20250224131420256-1314204608.png)