无限微积分由 \(\mathrm{D}f(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h}\) 所定义的微分算子 \(\mathrm{D}\) 的性质,有限微分则是由 \(\Delta f(x) = f(x+h) - f(x)\) 所定义的差分算子 \(\Delta\) 的性质。
微分算子作用在幂函数上的结果可以表示为 \(\mathrm{D}(x^m)=mx^{m-1}\),而差分算子在 \(h \to 1\) 时能够达到的极限为 \(h=1\),所以差分算子作用在幂函数上的结果类似于 \(\Delta(x^3)=(x+1)^3-x^3=3x^2+3x+1\)。但有一类幂次在差分算子的作用下可以很好的变换,有利于处理和式。
下降阶乘幂与上升阶乘幂
下降阶乘幂由
所定义。差分算子 \(\Delta\) 作用在下降阶乘幂上能拥有与微分算子 \(\mathrm{D}\) 作用在幂函数上类似的形式,如下所示。
反之,我们在进行差分逆运算时(对应微分之于积分,即求和),其一般运算法则为
当 \(m=-1\) 时我们令 \(\Delta f(x) = f(x+1) - f(x) = x^{\underline{-1}}\),则有 \(f(x) = \frac{1}{1} + \frac{1}{2} + \cdots + \frac{1}{x} = H_x\) 满足条件。所以
在微积分中,\(e^x\) 的导数是其自身,那么什么函数的差分是其自身呢?我们令
类似的,上升阶乘幂由
所定义。
分部求和法
参考微积分中的分部积分法,我们可以利用分布求和法来进行和式求解。我们考虑如下差分
我们定义一个移位运算
对等式两边求和,则我们可以得到不定求和的分部运算法则
例 1:计算 \(\sum_{k=0}^n k2^k\)。
首先我们计算不定求和
接着代入区间 \([0,n]\) 计算结果
例 2:计算 \(\sum_{k=0}^{n-1} kH_k\)。
首先我们计算不定求和
接着代入区间 \([0,n]\) 计算结果
例 3:计算 \(\sum_{k=1}^n\frac{2k+1}{k(k+1)}\)
斯特林数
第二类斯特林数记作 \(S(n,k)\),表示将 \(n\) 个两两不同的元素,划分为 \(k\) 个互不区分的非空子集的方案数。其满足的递推式为
例 4:已知 \(z^n = \sum_{k=0}^{n} S(n,k) \cdot z^{\underline{k}}\),求证 \(S(n,k)\) 对于 \(n\geq1,k\geq1\) 满足 \(S(n,k)=S(n-1,k-1)+k(n-1,k)\)。
我们使用数学归纳法进行证明:
-
当 \(n=1\) 时,我们有 \(z^1 = \sum_{k=0}^1S(n,k) = S(1,0)+S(1,1)=1\)。我们已知 \(S(1,0)=0\),则 \(S(1,1)=1\)。
-
当 \(n=2\) 时,我们有 \(z^2=S(2,0)+S(2,1)\cdot z+S(2,2)\cdot z(z-1)\),比较系数后我们有 \(S(2,0)=0, S(2,1)=1, S(2,2)=1\),则
\[\left.\begin{matrix} F(2,1) = F(1,0) + 1\cdot F(1,1) = 1 \\ F(2,2) = F(1,1) + 2\cdot F(1,2) = 1 \end{matrix}\right\}\Rightarrow F(2,k) = F(1,k-1) + k\cdot F(1,k). \]符合初值。
-
我们假设命题在 \(n=m\) 时成立。
-
当 \(n=m+1\) 时,有
\[\begin{align*}z^{m+1} = z^m \cdot z &= z\sum_{k=0}^{m} F(m,k)\cdot z^{\underline{k}} \\&= \sum_{k=0}^{m} F(m,k)\cdot z\cdot z^{\underline{k}} \\&= \sum_{k=0}^{m} F(m,k)\cdot (z-k+k)\cdot z^{\underline{k}} \\&= \sum_{k=0}^{m} F(m,k)\cdot (z-k)\cdot z^{\underline{k}} + k\sum_{k=0}^{m} F(m,k)\cdot z^{\underline{k}} \\&= \sum_{k=0}^{m} F(m,k)\cdot z^{\underline{k+1}} + k\sum_{k=0}^{m} F(m,k)\cdot z^{\underline{k}} \\&= \sum_{k=1}^{m+1} F(m,k-1)\cdot z^{\underline{k}} + k\sum_{k=1}^{m} F(m,k)\cdot z^{\underline{k}} \\&= F(m,m) \cdot z^{\underline{m+1}} + \sum_{k=1}^{m} [F(m,k-1)+k\cdot F(m,k)]\cdot z^{\underline{k}}. \end{align*} \]比较同幂次的系数,得
\[F(m+1,k) = F(m,k-1) + k \cdot F(m,k). \]
命题成立。
第一类斯特林数记作 \(s(n,k)\),表示将 \(n\) 个两两不同的元素,划分为 \(k\) 个互不区分的非空轮换的方案数。其满足的递推式为
例 5:已知 \(z^{\underline{n}} = \sum_{k=0}^{n} s(n,k) \cdot z^{k}\),求证 \(s(n,k)\) 对于 \(n\geq1,k\geq1\) 满足 \(s(n,k) = s(n-1,k-1) + (n-1)s(n-1,k)\)。
类似地,我们使用数学归纳法进行证明,使用 \(n-1\) 替换等式中的 \(n\),有
比较系数后得到
命题成立。


![[QOJ 8366] 火车旅行](https://img2024.cnblogs.com/blog/3584318/202502/3584318-20250224140737540-1060414145.png)
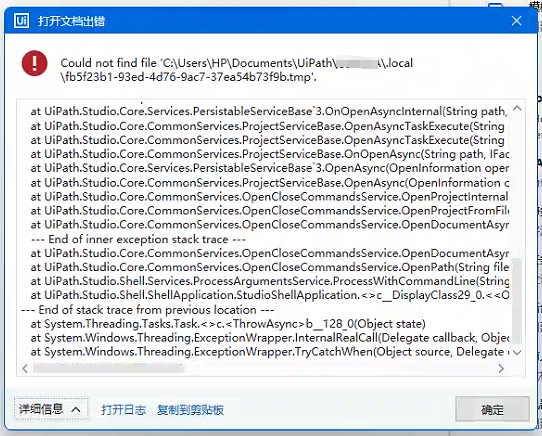

![BUUCTF-RE-[2019红帽杯]easyRE](https://img2024.cnblogs.com/blog/3596699/202502/3596699-20250224131420256-1314204608.png)
