2025省选模拟15

2025省选模拟15

\(T1\) P1045. 数 \(100pts\)

• 原题： SP6408 KKKCT2 - Counting Triangles 2 | SP5464 CT - Counting triangles

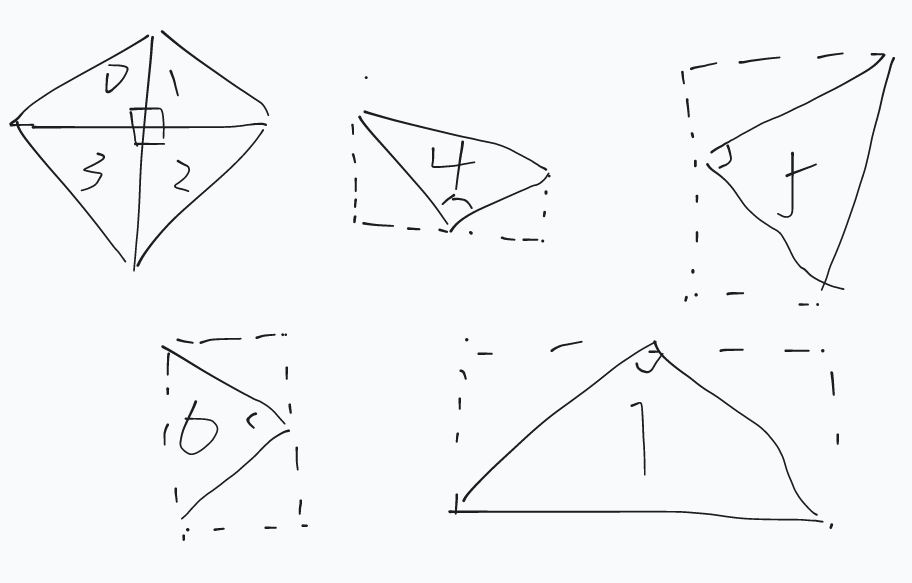
• 考虑枚举直角顶点 \((i,j),0 \le i \le x,0 \le j \le y\)，然后分为了 \(8\) 种贡献情况。

  

• 设 \(\begin{cases} a=\min(i,y-j) \\ b=\min(x-i,j) \\ c=\min(i,j) \\ d=\min(x-i,y-j) \end{cases}\) ， \(8\) 种情况的贡献分别为 \(a,d,b,c,ad,bd,ac,ad\) ，加起来后得到 \((a+b+1)(c+d+1)-1\) ，但没有什么可以优化的地方。

• 观察乘积项，以 \(ac\) 为例，考虑固定 \(i\) 这个常量，统计 \(j\) 的贡献，分讨 \(0,y-j,j,y\) 划分成的三个区间内部的转移即可。

  点击查看代码

  const ll p=20120712;
  ll s1(ll n)
  {return n*(n+1)/2;
  }
  ll s2(ll n)
  {return n*(n+1)*(2*n+1)/6;
  }
  ll ask(ll up,ll a,ll b)
  {ll ans=0;ans+=s1(min(a,up))+max(0ll,(up-a))*a;//2e8ans+=s2(min(min(a,b)-1,up));//2e12if(min(min(a,b)-1,up)<min(max(a,b),up))ans+=(min(min(a,b)-1,up)+1+min(max(a,b),up))*(min(max(a,b),up)-min(min(a,b)-1,up))/2*min(a,b);//2e12ans+=max(0ll,(up-max(a,b)))*a*b;//1e12return ans;
  }
  int main()
  {
  #define Isaac
  #ifdef Isaacfreopen("count.in","r",stdin);freopen("count.out","w",stdout);
  #endifint t,x,y,i,j;ll ans;cin>>t;for(;t>=1;t--){cin>>x>>y;  ans=0;// a=min(i,y-j),b=min(x-i,j),c=min(i,j),d=min(x-i,y-j)for(i=0;i<=x;i++){ans+=ask(y,i,x-i);// bc+cans+=ask(y,x-i,i);// ad+d}for(i=0;i<=y;i++){ans+=ask(x,y-i,i);// ac+aans+=ask(x,i,y-i);// bd+b}cout<<ans%p<<endl;}	return 0;
  }
  

\(T2\) P1047. 树 \(10pts\)

• 部分分

  • \(10pts\) ：去大样例里把 \(n \le 8\) 的数据粘过来。

• 正解

  • 拼劲全力无法战胜。

  

  

  

  • 解法 \(5\) 中提到的在输出答案的时候除以 \(n\) 的处理方法同 暑假集训CSP提高模拟3 T1 P117. abc猜想 。
  点击查看 std

  #include <bits/stdc++.h>
  using namespace std;
  int n, T;
  long long mod, mat[31][2][2];
  int main() {freopen("tree.in", "r", stdin);freopen("tree.out", "w", stdout);ios::sync_with_stdio(0);cin.tie(NULL);cout.tie(NULL);mat[0][0][0] = 0;mat[0][0][1] = 1;mat[0][1][0] = 1;mat[0][1][1] = 1;cin >> T;while (T--) {cin >> n >> mod;mod *= n;int tmp = n;vector<int> pr, fac;for (int i = 2; i <= sqrt(tmp); i++)if (tmp % i == 0) {pr.push_back(i);while (tmp % i == 0) tmp /= i;}if (tmp != 1) pr.push_back(tmp);for (int i = 1; i <= sqrt(n); i++)if (n % i == 0) {fac.push_back(i);if (i * i != n) fac.push_back(n / i);}for (int i = 1; i < 31; i++) {mat[i][0][0] = (__int128(mat[i - 1][0][0]) * mat[i - 1][0][0] +__int128(mat[i - 1][0][1]) * mat[i - 1][1][0]) %mod;mat[i][0][1] = (__int128(mat[i - 1][0][0]) * mat[i - 1][0][1] +__int128(mat[i - 1][0][1]) * mat[i - 1][1][1]) %mod;mat[i][1][0] = (__int128(mat[i - 1][1][0]) * mat[i - 1][0][0] +__int128(mat[i - 1][1][1]) * mat[i - 1][1][0]) %mod;mat[i][1][1] = (__int128(mat[i - 1][1][0]) * mat[i - 1][0][1] +__int128(mat[i - 1][1][1]) * mat[i - 1][1][1]) %mod;}long long ans = 0;for (auto i : fac) {int phi = n / i;for (auto j : pr)if (phi % j == 0) phi = phi / j * (j - 1);long long f[2] = {1, 1}, g[2];for (int j = 0; j < 31; j++)if (i + i - 2 & (1 << j)) {g[0] = (__int128(f[0]) * mat[j][0][0] +__int128(f[1]) * mat[j][1][0]) %mod;g[1] = (__int128(f[0]) * mat[j][0][1] +__int128(f[1]) * mat[j][1][1]) %mod;f[0] = g[0];f[1] = g[1];}ans = (ans + __int128(phi) * (f[0] + f[0] + f[1] - 2)) % mod;}cout << ans / n << '\n';}
  }

\(T3\) P1046. 书 \(0pts\)

• 原题： HDU2484 Build the Tower

• 对书进行排序后，有 \(f_{S}=1+\frac{1}{c+1}(f_{S \bigoplus \operatorname{lowbit}(S)}+\sum\limits f_{S|(1<<i)})\) 。从 \(S \bigoplus \operatorname{lowbit}(S)\) 向 \(S\) 连一条有向边得到树形关系后考虑树上高斯消元。

• 观察到实际上栈顶元素和厚度和相同时，后续决策是相同的，于是状态数从 \(O(2^{n})\) 优化到了 \(O(nm)\) 。

• 此时有 \(f_{x}=1+\frac{1}{c+1}f_{fa_{x}}+\frac{\sum\limits_{y \in \operatorname{Son}(x)}f_{y}}{c+1}=a_{x}f_{fa_{x}}+b_{x}\) ，解得 \(a_{x}=\frac{1}{(c+1)(1-\frac{1}{c+1}\sum\limits_{y \in \operatorname{Son}(x)}a_{y})},b_{x}=\frac{1+\frac{1}{c+1}\sum\limits_{y \in \operatorname{Son}(x)}b_{y}}{1-\frac{1}{c+1}\sum\limits_{y \in \operatorname{Son}(x)}a_{y}}\) 。

• 实际实现时，可以设 \(f_{i,j}\) 表示栈顶为 \(i\) 厚度和为 \(j\) 的期望，从 \(f_{k,j+b'_{k}}\) 转移而来；加入一个根节点 \(n+1\) 取 \(f_{n+1,0}\) 作为答案。

  点击查看代码

  pair<int,int>c[110];
  double a[110][110],b[110][110];
  int main()
  {
  // #define Isaac
  #ifdef Isaacfreopen("book.in","r",stdin);freopen("book.out","w",stdout);
  #endifint n,m,cnt,i,j,k;double suma,sumb;while(cin>>n>>m){c[n+1].first=101;for(i=1;i<=n;i++)  cin>>c[i].first>>c[i].second;sort(c+1,c+1+n);for(i=1;i<=n+1;i++){for(j=0;j<=m;j++){cnt=suma=sumb=0;for(k=1;k<=i;k++)  cnt+=(c[k].first<c[i].first);for(k=1;k<=i;k++){if(c[k].first<c[i].first&&j+c[k].second<=m){suma+=a[k][j+c[k].second];sumb+=b[k][j+c[k].second];}}a[i][j]=1/(1-suma/(cnt+1))/(cnt+1);b[i][j]=(sumb/(cnt+1)+1)/(1-suma/(cnt+1));}}if(b[n+1][0]>18000)  cout<<"INF"<<endl;else  printf("%.3lf\n",b[n+1][0]);}return 0;
  }
  

总结

• \(T2\) 尝试拉格朗日插值但因为不保证模数是质数，遂无果。