PKU ACM Teams Excursion

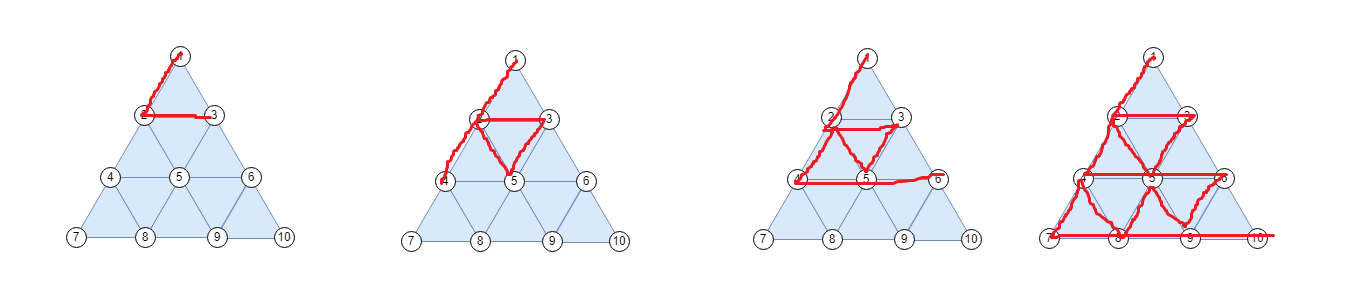
• 有向无环图的必经点与必经边：路径条数取模法
• memset的时候int/long long要一一对应
• 分两种情况讨论：一种是两条路线连在一起，视为一条路线处理即可；另一种是两条路线相互分隔，可以枚举分界点
• 要多测的题目提交之前可以先复制样例测试几次

#include <bits/stdc++.h>
using namespace std;
vector<int>a[100005],c[100005];
const int mod=1000000007;
int u[200005],v[200005],w[200005];
int d[100005],pre1[100005],pre2[100005],dis[100005],g[2][100005][2],n;
long long f[2][100005];
typedef pair<int,int> pii;
map<pii,bool>h;
bool e[100005];
void topsort(int s,int opt)
{queue<int>q;for(int i=0;i<n;i++){if(d[i]==0){q.push(i);}}memset(f[opt],0,sizeof(long long)*n);f[opt][s]=1;if(!opt){memset(dis,0x3f,sizeof(int)*n);dis[s]=0;}while(q.size()){int n1=q.front();q.pop();for(int i=0;i<a[n1].size();i++){(f[opt][a[n1][i]]+=f[opt][n1])%=mod;d[a[n1][i]]--;if(d[a[n1][i]]==0){q.push(a[n1][i]);}if(!opt){if(dis[n1]+c[n1][i]<dis[a[n1][i]]){dis[a[n1][i]]=dis[n1]+c[n1][i];pre1[a[n1][i]]=n1;pre2[a[n1][i]]=c[n1][i];}}}}
}
int b[100005],sum[100005],len,q;
void dp(int opt)
{for(int i=1;i<=len;i++){sum[i]=sum[i-1]+b[i];g[opt][i][0]=g[opt][i-1][0]+e[i]*b[i];auto check=[i](int x){return sum[i]-x>=q;};int p=partition_point(sum,sum+i+1,check)-sum;if(p==0){g[opt][i][1]=0;}else{g[opt][i][1]=min(g[opt][i-1][1]+e[i]*b[i],g[opt][p-1][0]+e[p]*(sum[i]-sum[p-1]-q));}}
}
int main()
{ios::sync_with_stdio(false);cin.tie(0);int T;cin>>T;while(T--){int m,s,t;cin>>n>>m>>s>>t>>q;for(int i=1;i<=m;i++){cin>>u[i]>>v[i]>>w[i];}for(int i=0;i<n;i++){a[i].clear();c[i].clear();d[i]=0;}for(int i=1;i<=m;i++){a[u[i]].push_back(v[i]);c[u[i]].push_back(w[i]);d[v[i]]++;}topsort(s,0);for(int i=0;i<n;i++){a[i].clear();d[i]=0;}for(int i=1;i<=m;i++){a[v[i]].push_back(u[i]);d[u[i]]++;}topsort(t,1);if(dis[t]>1000000000){cout<<-1<<endl;continue;}h.clear();for(int i=1;i<=m;i++){if(f[0][t]==f[0][u[i]]*f[1][v[i]]%mod){h[pii(u[i],v[i])]=true;}}len=0;int p=t;while(p!=s){len++;b[len]=pre2[p];if(h.find(pii(pre1[p],p))!=h.end()){e[len]=true;}else{e[len]=false;}p=pre1[p];}dp(0);reverse(b+1,b+len+1);reverse(e+1,e+len+1);dp(1);int ans=INT_MAX;for(int i=1;i<len;i++){ans=min(ans,g[0][i][1]+g[1][len-i][1]);}q*=2;dp(1);cout<<min(ans,g[1][len][1])<<endl;}return 0;
}