NFSP

news/2025/2/28 16:09:27/文章来源:https://www.cnblogs.com/usersname/p/18743444

NSFP算法

论文名称：《Deep Reinforcement Learning from Self-Play in Imperfect-Information Games》

这是一篇博弈论和强化学习交叉的文章，网上的资料比较少，但是确实是对手建模的重要算法之一。虽然后面的PSRO算法指出NFSP是PSRO的一个特例，但是个人觉得还是很有学习的必要。

一、基本问题

在多智能体独立学习算法中，环境的非平稳性一直是一个非常大的问题。传统的强化学习算法直接应用于多智能体环境中，由于环境不符合马尔可夫过程，算法的收敛没有理论的保证。二在博弈环境中，传统的强化学习算法往往会过拟合对手的策略，进一步放大了环境的非平稳性。

纳什均衡，是博弈论中的术语，是指智能体在对手做出任何行动下，执行的策略依旧可以最大化收益的一种状态。在多智能体环境下，模型收敛的目标就是纳什均衡。

NFSP算法就是作者提出的一种端到端的算法，可以在没有任何先验输入的情况下，收敛到纳什均衡。

二、基础知识

虚拟博弈算法（Fictitious play， FP）

FP算法是一个经典的博弈论算法。这个算法更具对手的策略计算只身的最佳响应策略，并保存到一个缓冲池中。然后取缓冲池中的平均策略（这里有说是按一定比例混合平均策略的，但是都差不多），作为下一轮的策略，不断迭代，最终可以收敛到纳什均衡。FP算法的流程图表示如下：

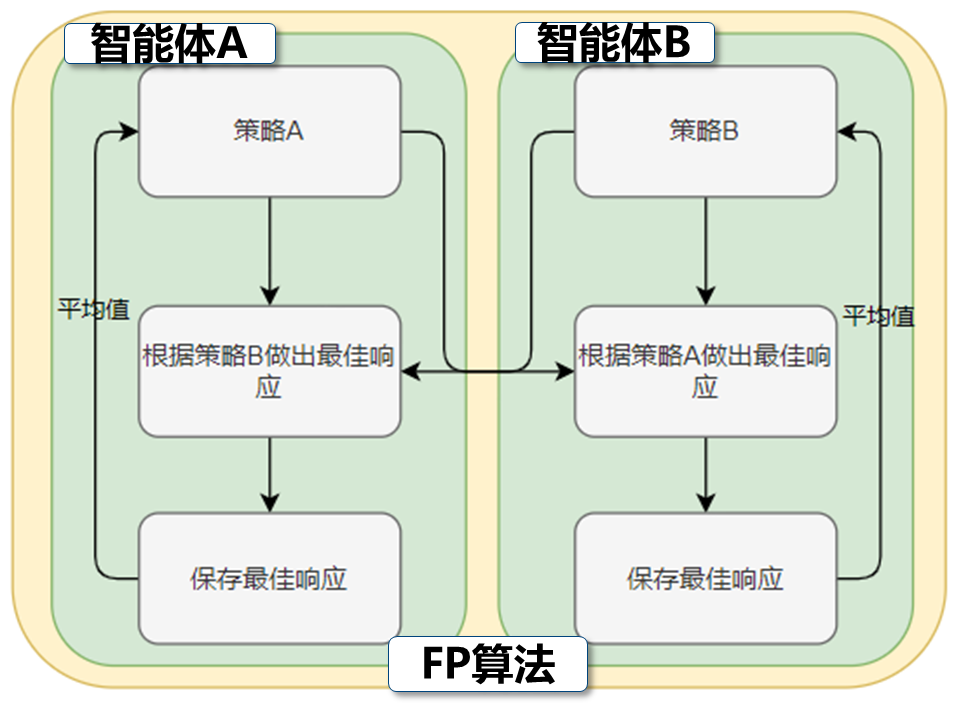
显然，FP算法有明显的缺点：
1. 必须知道全局的动作和收益，因为如果不知道全局的动作和收益，就没有办法计算最佳响应策略。
2. 不适用于扩展性博弈和重复博弈，并且FP算法只能处理两个智能体的情况。扩展性和重复博弈都要求智能体可以多次选择动作，但是FP算法只能求解一次博弈的均衡策略（迭代是为了求解这个均衡策略）。
举个具体的例子来说：

动作A 动作B

动作A 1，1 1，1

动作B 0，2 2，0

上面的表格是一个进攻防御模型的收益矩阵，行表示进攻方，可以选择动作A和动作B。列表示防御方，可以选择动作A和动作B。表格中的数值表示收益，比如第一列，第二行中（0，2）表示如果防御方选择动作B，进攻方选择动作A。那么，防御方收益为0，进攻方收益为2。

在这个模型中，进攻方选择动作A的收益分别为（1，2），大于等于动作B的收益（1，0），是一个弱优势策略。所以，如果进攻方绝对理性，就一定会选择动作A。防御方考虑到进攻方一定会选择动作A后也会选择动作A，应为动作A的收益1大于动作B的收益0。因此，在这个模型中动作A就是纳什均衡策略。

但是以上只是理论分析，实际上适用FP算法迭代100次之后，进攻方和防御方选择各个策略的概率如下：

动作A 动作B

进攻方 0.995 0.005

防御方 0.998 0.002

可以看到，FP算法迭代后，选择动作A的概率逐渐逼近1。
虚拟自博弈算法（Fictitious self play， FSP）
- 自博弈
  
  就是智能体和自己（也可以是以前的自己）互相对抗，使得只身的策略收敛到纳什均衡的一种方法。
虚拟自博弈就是将自博弈的过程应用在了FP算法。同时FPS算法将求解最优策略的过程替换为了强化学习算法。

虚拟自博弈的流程图如下：