💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码及文献
💥1 概述
文献来源:


自过去十年以来,启发式优化算法正在国际计算智能界的研究人员中引起涟漪。启发式算法在各个领域的研究工作和应用是惊人的。启发式算法因其随机性和简单性而越来越受欢迎。根据无免费午餐定理(NFLT)(Wolpert and Macready,1997),单一算法无法解决所有优化问题。简单来说,如果一个优化算法以高性能解决了某个问题,那么它在解决其他类型的优化问题时很有可能表现不佳。因此,研究人员发明了许多优化算法,并且每年都有新的算法被提出。著名的优化算法包括受鸟类和鱼类社会行为启发的PSO(Kennedy and Eberhart,1995),基于蚂蚁搜索行为的ACO (Dorigo and Caro, 1995),BBO (Simon, 2008)灵感来自物种的分布和迁移模型,以及DE(Storn and Price, 1995)和GA(Tang, 1996) 这是由进化论驱动的。此外,还有数学驱动的优化算法,如SCA(Mirjalili,2016),它在数学上模拟正弦和余弦函数的行为。此外,Mirjalili等人(2017)最近开发了一种基于salps的组和导航行为的新型元启发式算法,即SSA。它们已被应用于解决计算机科学和其他研究领域的各种问题,如电子、生物学和石油工业。在计算机科学中,它们被用于函数优化(Du和Li,2008; 姚等,1999),控制目标(宝江和世勇,2007; 卡拉库祖,2008年; Kim等人,2008),模式识别(Liu等人,2008; Tan和Bhanu,2006),过滤器建模(Kalinlia和Karabogab,2005)和图像的最佳处理(Cordon等人,2006; Nezamabadi-pour 等人,2006 年)。在电子科学中,负载调度(Beigvand 等人,2016,2017)和最优潮流(Bhowmik and Chakraborty,2015)问题已通过优化算法得到有效解决。
所有优化算法都由随机的代理群体组成,用于在搜索空间中查找候选解决方案。该过程从问题域中的代理初始化开始。然后,该算法经过多次迭代,每次迭代都给出可行的候选解决方案,直到满足条件的结束。所有迭代中的最佳可行候选解是最优解。令人惊讶的是,随机算法由一些基本步骤组成,例如探索和开发。探索是指算法的搜索空间。在此阶段,候选解决方案将经历许多更改。此外,开发是围绕不同的可行解决方案找到局部最优的能力。候选解决方案会导致开发阶段的微小变化。已经看到,如果优化算法具有良好的探索能力,那么它将缺乏良好的开发能力,反之亦然(Eiben and Schippers, 1998)。因此,它们彼此成反比。以前,研究人员分别使用随机游走和梯度下降方法来改善勘探和开发。但它的缺点是增加了算法的整体计算成本。自过去十年以来,研究人员正在使用混沌地图来增加搜索空间的多样化和局部开发,以找到最佳解决方案(Mirjalili 等人,2017 年; 甘多米等人,2012 年)。
混沌理论是对动态系统的研究。这些系统的有趣特性是,当系统中发生微小变化时,整个系统都会受到影响。简而言之,初始参数的变化会在整个系统中产生变化。此外,随机性对于混沌系统不是必需的,而确定性系统也表现出混沌行为(Kellert,2017)。该优化算法利用混沌图的初始参数敏感度(IPS)特性,快速开发、全局探索,缓解局部极小值陷阱问题。
元启发式算法在基准函数上显示出良好的结果,但它们在实际问题上表现不佳。实际问题是检查优化算法解决问题能力的实际测试。
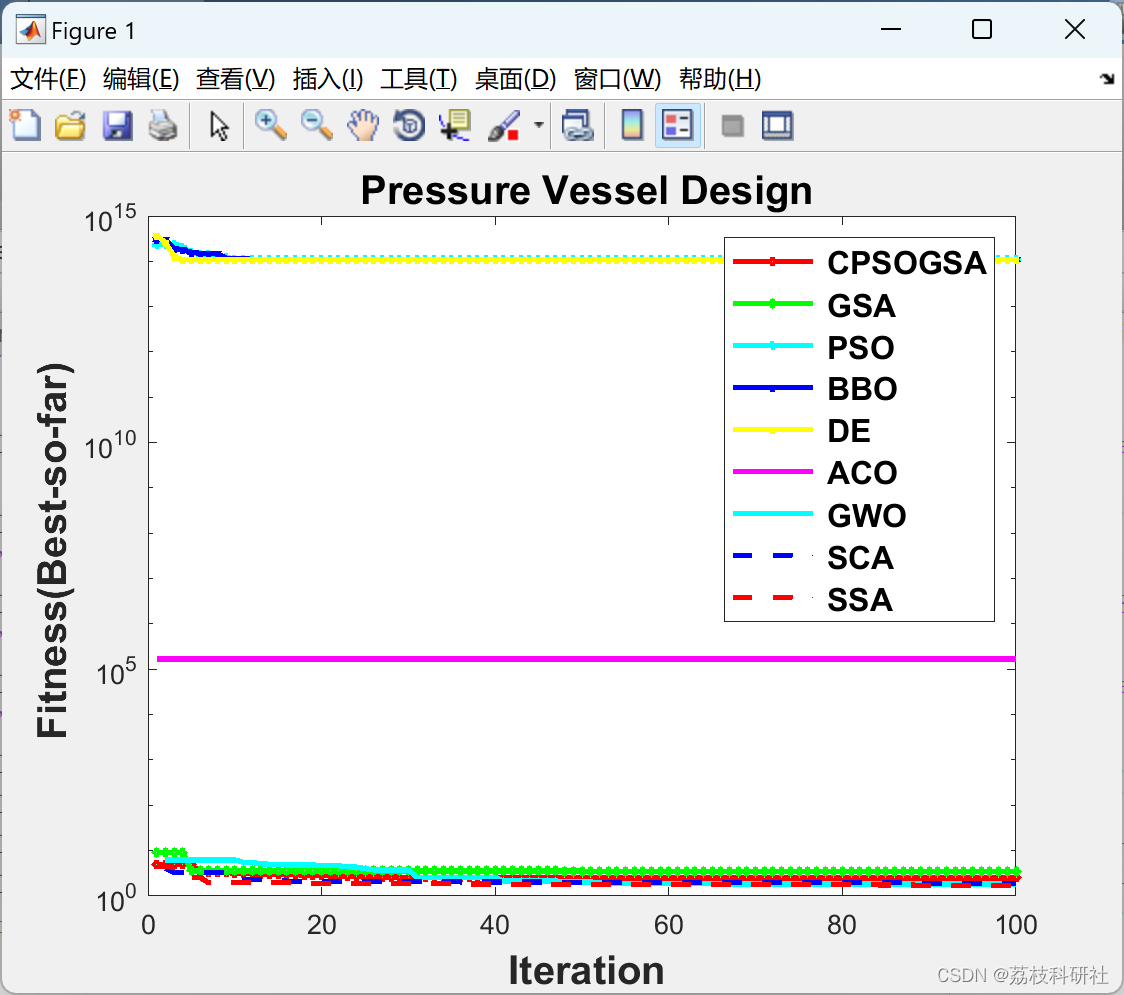
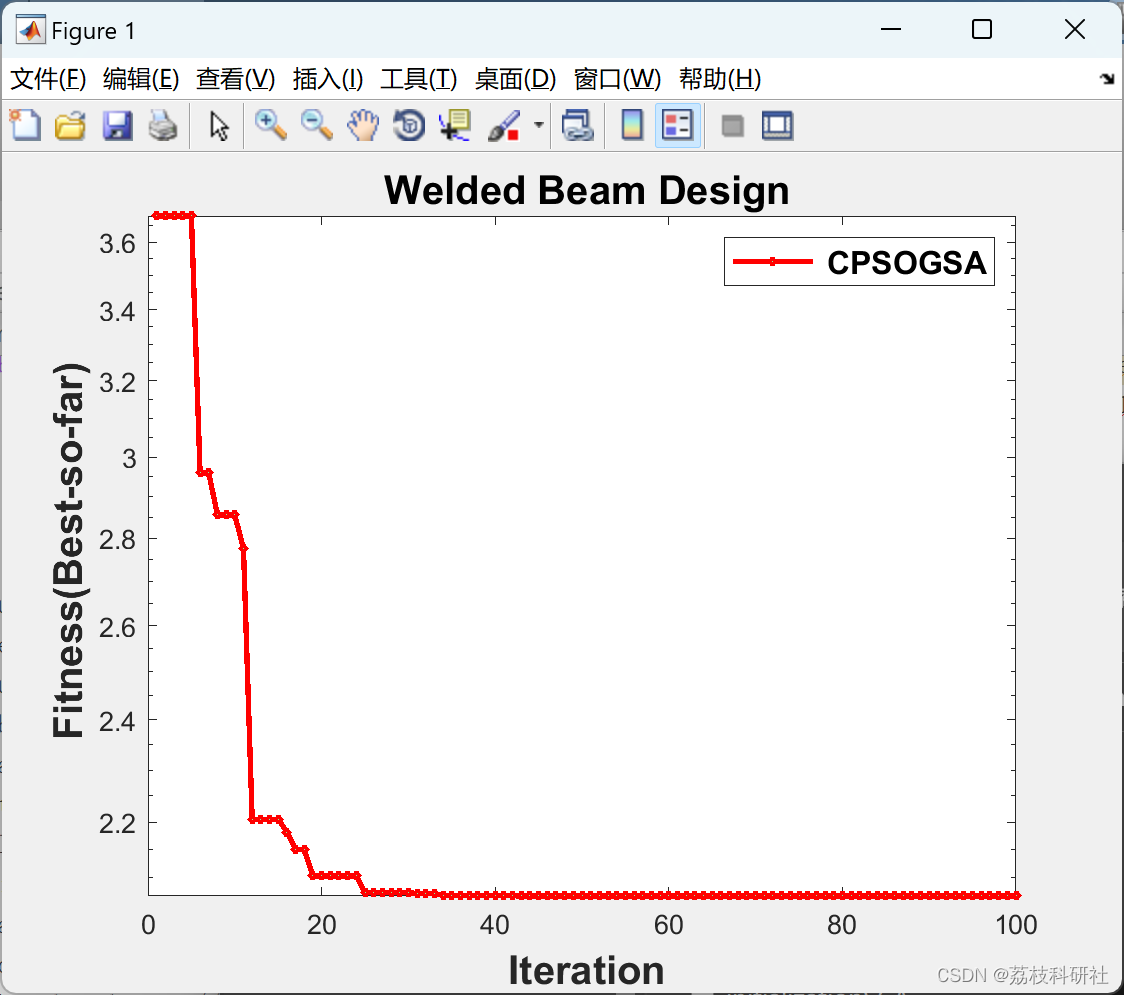
研究人员使用各种优化技术,如GA,PSO,DE,GSA,BBO,来解决其他领域的应用问题。大多数算法本质上是进化的,但GSA是一种基于物理学的最新元启发式算法。GSA(Rashedi 等人,2009 年)是一种优化算法,其灵感来自牛顿的万有引力定律和运动定律。标准GSA中增加了<>个混沌图,并已应用于三个工程设计问题,用于研究其杂交潜力和处理复杂的非线性基准。所有这些问题都有未知的搜索空间,非常适合检查算法的问题解决能力。此外,还将检查CGSA的约束处理和工程设计问题的参数优化。
📚2 运行结果

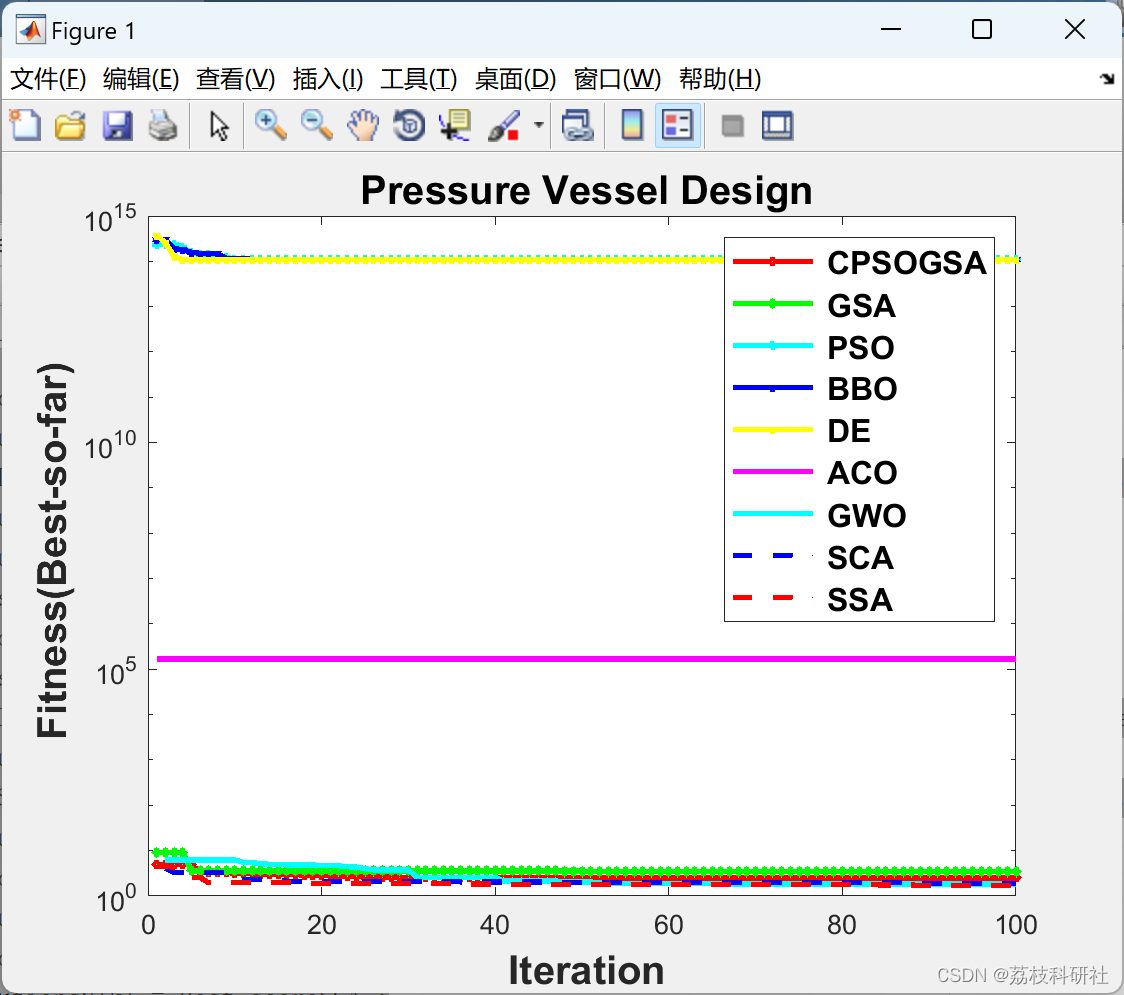
部分代码:
N = 50; % Number of Searcher Agents "
Max_Iteration = 100; % Maximum number of "iterations"
Q=1; % ACO Parameter
tau0=10; % Initial Phromone (ACO)
alpha=0.3; % Phromone Exponential Weight (ACO)
rho=0.1; % Evaporation Rate (ACO)
beta_min=0.2; % Lower Bound of Scaling Factor (DE)
beta_max=0.8; % Upper Bound of Scaling Factor (DE)
pCR=0.2; % Crossover Probability (DE)
ElitistCheck=1; % GSA Parameter
Rpower=1; % GSA Parameter
min_flag=1; % 1: minimization, 0: maximization (GSA)
Algorithm_num=2; %% These are 10 chaotic maps mentioned in the paper. So, change the value of Algorithm_num from 2 to 11 as 1 is for standard GSA.
chValueInitial=20; % CGSA
Benchmark_Function_ID=1 %Benchmark function ID
RunNo = 20;
for k = [ 1 : 1 : RunNo ]
% % %
[gBestScore,gBest,GlobalBestCost]= CPSOGSA(Benchmark_Function_ID, N, Max_Iteration);
BestSolutions1(k) = gBestScore;
[Fbest,Lbest,BestChart]=GSA(Benchmark_Function_ID,N,Max_Iteration,ElitistCheck,min_flag,Rpower);
BestSolutions2(k) = Fbest;
[PcgCurve,GBEST]=pso(Benchmark_Function_ID,N,Max_Iteration);
BestSolutions3(k) = GBEST.O;
[BestCost,BestSol] = bbo( Benchmark_Function_ID, N, Max_Iteration);
BestSolutions4(k) = BestSol.Cost;
[BestSolDE,DBestSol,BestCostDE] = DE(Benchmark_Function_ID, N, Max_Iteration,beta_min,beta_max,pCR);
BestSolutions5(k) = BestSolDE.Cost ;
[BestSolACO,BestAnt,BestCostACO] = ACO(Benchmark_Function_ID, N, Max_Iteration,Q,tau0,alpha,rho);
BestSolutions6(k) = BestSolACO.Cost ;
[Best_score,Best_pos,SSA_cg_curve]=SSA(Benchmark_Function_ID, N, Max_Iteration);
BestSolutions7(k) = Best_score ;
[Best_scoreSCA,Best_pos,SCA_cg_curve]=SCA(Benchmark_Function_ID, N, Max_Iteration);
BestSolutions8(k) = Best_scoreSCA ;
[Best_scoreGWO,Best_pos,GWO_cg_curve]=GWO(Benchmark_Function_ID, N, Max_Iteration);
BestSolutions9(k) = Best_scoreGWO ;
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]Rather, S. and Bala, P. (2020), "Swarm-based chaotic gravitational search algorithm for solving mechanical engineering design problems", World Journal of Engineering, Vol. 17 No. 1, pp. 97-114.