众所周知,自然常数——\(e = \lim\limits_{n\to\infty}(1 + \frac{1}{n})^n\)。
不妨设 \(x_n=(1+\frac{1}{n})^n\)(\(n\ge 1\))。
那么 \(x_n\) 的上界是多少?
\(\because\) 单调有界数列必定收敛。(收敛的定义:指会聚于一点,向某一值靠近。)
\(\therefore\) 我们先证明其单调性。
由基本不等式,得:
\(\begin{aligned} x_n=(1+\frac{1}{n})^n=(\frac{n+1}{n})^n\cdot 1 &\le(\frac{n\cdot\frac{n+1}{n}+1}{n+1})^{n+1}\\ &=(\frac{n+1+1}{n+1})^{n+1}\\ &=(1+\frac{1}{n+1})^{n+1}\\ &=x_{n+1} \end{aligned}\)
当且仅当,\(\frac{n+1}{n}=1\) 时,等号成立。
但是 \(\frac{n+1}{n}=1\) 无解,所以 \(x_n<x_{n+1}\)。
So,\(x_n\) 是单调递增的。
这样的话,下界就是 \(x_1=2\)。
我们再来搞上界。
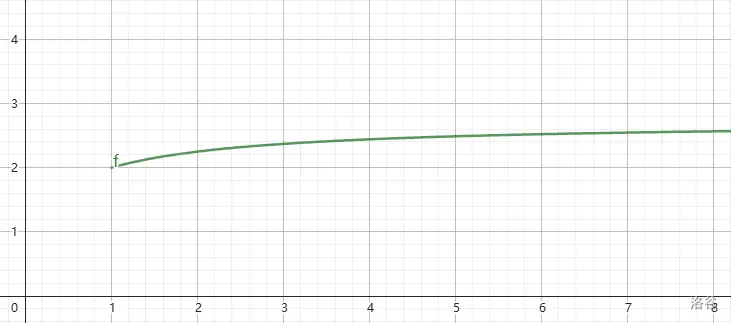
这是 \(x_n\) 的图像。
通过图像,可以很明显地看出 \(x_n\) 的增长速度越来越慢。那么,根据直觉,\(x_n\) 应该是有一个上界。
接下来来推一下 \(x_n\) 是否有上界。
由二项式定理得:
\(\begin{aligned} x_n &=(1+\frac{1}{n})^n\\ &=1+C_n^1(\frac{1}{n})+C_n^2(\frac{1}{n})^2+\cdots+C_n^k(\frac{1}{n})^k+\cdots+(\frac{1}{n})^n\\ &=1+n\cdot\frac{1}{n}+\frac{n!}{2!(n-2)!}\cdot\frac{1}{n^2}+\cdots+\frac{n!}{k!(n-k)!}\cdot\frac{1}{n^k}+\cdots+\frac{1}{n^n}\\ &=1+1+\frac{1}{2!}\cdot(n-1)n\cdot\frac{1}{n^2}+\cdots+\frac{1}{k!}\cdot\prod\limits_{i=n-k+1}^ni\cdot\frac{1}{n^k}+\cdots+\frac{1}{n^n}\\ &=1+1+\frac{1}{2!}\cdot\frac{n-1}{n}+\cdots+\frac{1}{k!}\cdot\frac{\prod\limits_{i=n-k+1}^{n-1}i}{n^{k-1}}+\cdots+\frac{1}{n^n}\\ &=1+1+\frac{1}{2!}\cdot(1-\frac{1}{n})+\cdots+\frac{1}{k!}\cdot\prod\limits_{i=1}^{k-1}(1-\frac{i}{n})+\cdots+\frac{1}{n^n} \end{aligned}\)
当 \(n\to\infty\) 时,\(x_n\le 1+1+\frac{1}{2!}+\cdots+\frac{1}{n!}<3\)。
(\(\frac{1}{2!}+\frac{1}{3!}+\cdots+\frac{1}{n!}<\frac{1}{2^1}+\frac{1}{2^2}+\cdots+\frac{1}{2^n}<1\))
\(x_n\) 的范围就是 \([2,3)\)。
所以 \(e\) 是有上界的。