大根堆/最大堆
以下是 大根堆(Heap)的C++代码模板,包含最大堆的基本操作(插入、删除堆顶、堆化等),注释详细说明关键步骤:
class MaxHeap {
private:vector<int> heap;// 获取父节点索引int parent(int i) { return (i - 1) / 2; }// 获取左子节点索引int left(int i) { return 2 * i + 1; }// 获取右子节点索引int right(int i) { return 2 * i + 2; }// 上浮操作:将节点i向上调整,维护堆性质void siftUp(int i) {while (i > 0 && heap[i] > heap[parent(i)]) {swap(heap[i], heap[parent(i)]);i = parent(i);}}// 下沉操作:将节点i向下调整,维护堆性质void siftDown(int i, int n) {int maxIndex = i;int l = left(i), r = right(i);if (l < n && heap[l] > heap[maxIndex]) maxIndex = l;if (r < n && heap[r] > heap[maxIndex])maxIndex = r;if (maxIndex != i) {swap(heap[i], heap[maxIndex]);siftDown(maxIndex, n); // 递归调整}}public:// 构造函数1:通过数组建堆MaxHeap(vector<int>& nums) {heap = nums;// 从最后一个非叶子节点开始调整for (int i = heap.size()/2 - 1; i >= 0; i--) {siftDown(i, heap.size());}}// 构造函数2:空堆MaxHeap() {}// 插入元素void push(int val) {heap.push_back(val);siftUp(heap.size() - 1); // 新元素上浮}// 删除堆顶元素(最大值)void pop() {if (heap.empty()) return;swap(heap[0], heap.back());heap.pop_back();siftDown(0, heap.size()); // 新堆顶下沉}// 获取堆顶元素(最大值)int top() {if (!heap.empty()) return heap[0];throw out_of_range("Heap is empty");}// 判断堆是否为空bool empty() { return heap.empty(); }// 获取堆大小int size() { return heap.size(); }
};
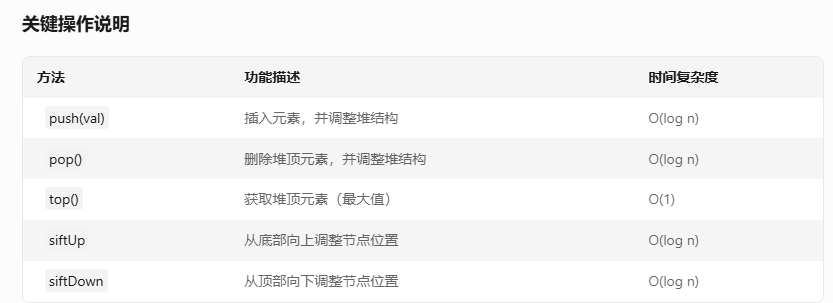
使用示例
int main() {// 示例1:通过数组建堆vector<int> arr = {3, 1, 6, 5, 2, 4};MaxHeap maxHeap(arr);while (!maxHeap.empty()) {cout << maxHeap.top() << " "; // 输出:6 5 4 3 2 1 maxHeap.pop();}// 示例2:逐个插入元素MaxHeap heap;heap.push(3);heap.push(1);heap.push(6);heap.push(5);cout << heap.top(); // 输出:6heap.pop();cout << heap.top(); // 输出:5return 0;
}

小根堆/最小堆
以下是 小根堆(Min Heap)的C++代码模板,包含插入、删除堆顶、堆化等基本操作,注释详细说明修改关键点:
class MinHeap {
private:vector<int> heap;// 获取父节点索引(与最大堆相同)int parent(int i) { return (i - 1) / 2; }// 获取左子节点索引(与最大堆相同)int left(int i) { return 2 * i + 1; }// 获取右子节点索引(与最大堆相同)int right(int i) { return 2 * i + 2; }// 上浮操作:修改比较符号为 <void siftUp(int i) {while (i > 0 && heap[i] < heap[parent(i)]) { // 仅此处改为 <swap(heap[i], heap[parent(i)]);i = parent(i);}}// 下沉操作:修改比较符号为 <void siftDown(int i, int n) {int minIndex = i;int l = left(i), r = right(i);// 比较子节点中的较小者if (l < n && heap[l] < heap[minIndex]) // 改为 <minIndex = l;if (r < n && heap[r] < heap[minIndex]) // 改为 <minIndex = r;if (minIndex != i) {swap(heap[i], heap[minIndex]);siftDown(minIndex, n); // 递归调整}}public:// 构造函数1:通过数组建堆(调整比较方向)MinHeap(vector<int>& nums) {heap = nums;// 从最后一个非叶子节点开始调整for (int i = heap.size()/2 - 1; i >= 0; i--) {siftDown(i, heap.size());}}// 构造函数2:空堆MinHeap() {}// 插入元素(与最大堆逻辑相同)void push(int val) {heap.push_back(val);siftUp(heap.size() - 1);}// 删除堆顶元素(最小值)void pop() {if (heap.empty()) return;swap(heap[0], heap.back());heap.pop_back();siftDown(0, heap.size());}// 获取堆顶元素(最小值)int top() {if (!heap.empty()) return heap[0];throw out_of_range("Heap is empty");}// 判断堆是否为空bool empty() { return heap.empty(); }// 获取堆大小int size() { return heap.size(); }
};
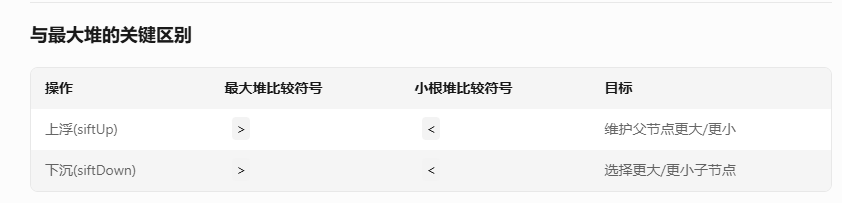
使用示例
int main() {// 示例1:通过数组建堆vector<int> arr = {3, 1, 6, 5, 2, 4};MinHeap minHeap(arr);while (!minHeap.empty()) {cout << minHeap.top() << " "; // 输出:1 2 3 4 5 6 minHeap.pop();}// 示例2:逐个插入元素MinHeap heap;heap.push(3);heap.push(1);heap.push(6);heap.push(5);cout << heap.top(); // 输出:1heap.pop();cout << heap.top(); // 输出:3return 0;
}