神秘另解集合，想出来一样的东西这辈子有了

P1600

考虑重链剖分。然后把每个路径给变成 \(O(\log n)\) 个重链，根据重链剖分的性质，每条重链的 dfs 序都为连续，所以把图画出来大概是像下图这样：

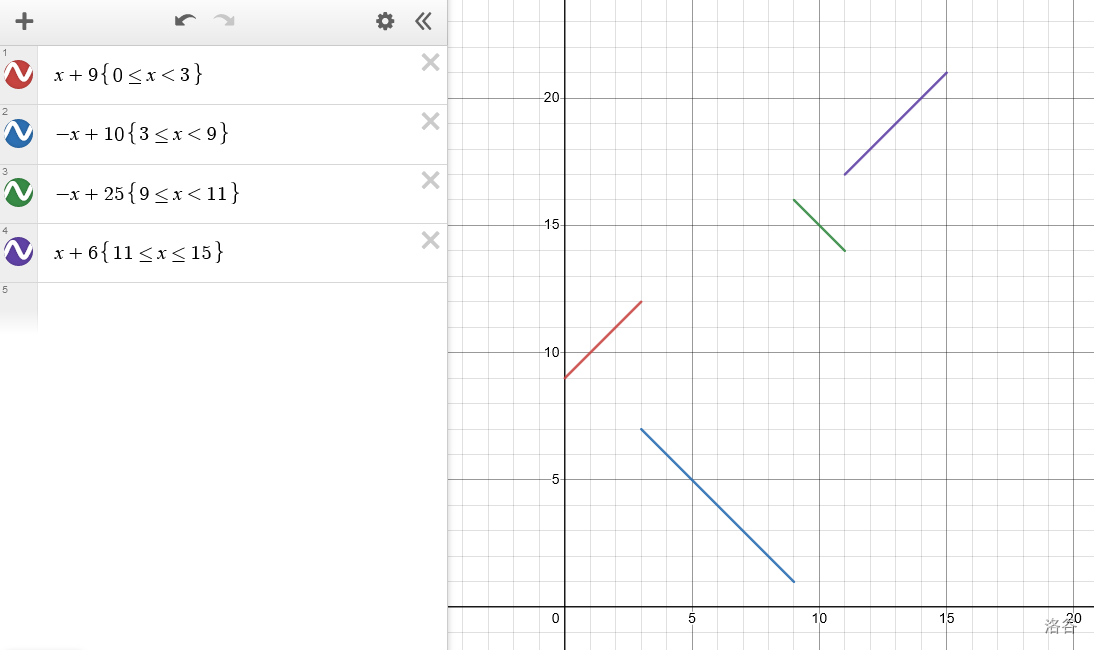
横轴是时间，纵轴是 dfs 序。一个时间 \(t\) 在节点 \(p\) 的人数就是经过 \((t,\text{dfn}_p)\) 的线段数量。线段数量为 \(O(m\log n)\)。

先旋转坐标轴，然后把横的竖的线段分开处理。下面只考虑横的。

将线段和询问的点先按纵坐标再按横坐标排序（可以使用计数排序使得线段数不会多一个 log）然后类似扫描线的做，可以关于线段数和询问点数线性。

复杂度 \(O(m\log n)\)。

AT_abc232_g

Solution 1

这是没过的。

先考虑这个 \(\bmod m\) 到底怎么用呢？发现 \(a_u+b_v\le 2m-2\)，所以 \(\bmod m\) 其实是在和 \(\ge m\) 的时候减去 \(m\)。一个点 \(u\) 的出边 \(u\to v\) 有两种：

• \(a_u+b_v<m\)，边权是 \(a_u+b_v\)。
• \(a_u+b_v\ge m\)，边权是 \(a_u+b_v-m\)。

一个自然的想法是将点按 \(b_i\) 排序，所以不妨让 \(b_i\) 单调不递减，然后发现对于固定的 \(u\)，这两个东西就分别构成前缀和后缀了！那么可以用一个类似“线段树优化建图”的“前后缀和优化建图”，图大概张这样：

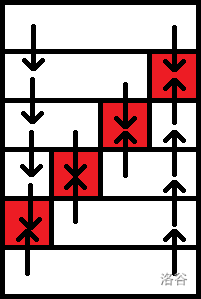
如图，红色格子从左到右代表真正的点，上面的代表前缀和，下面的代表后缀和。

其中指向真正点（红色格子）的边权为 \(b_i\)，其余边为 \(0\)。接下来枚举 \(u\)，找到两种出边情况的分割点，第一种连边长度为 \(a_u\)，第二种为 \(a_u-m\)。正确性显然。

但是发现有负权边，于是 SPFA，爆 TLE 了。

Solution 2

后来本来想要弃掉这个做法，但是突然想到怎么去掉负权边了。感觉很厉害。

显然上面负权边只出现在第二种情况，也就是连边到后缀的虚点的情况。挖掘这个边的性质。

设第一个第二类点为 \(r_u\)，则原图中 \(u\) 连到 \(v\ge r_u\) 的边权为 \(a_u+b_v-m\ge 0\)。容易发现取到 \(a_u+b_{r_u}=m\) 时可以使得这条边长度为 \(0\)，若想要优化的图中对应路径也为 \(0\)，必须经过的边权都为 \(0\)。

那么就不妨让之前的做法里后缀连向红点的边权全部为 \(0\)（下图中橙色边），相应地，也需要更改后缀连向小一点的后缀的边权。具体地，从 \(i\) 到 \(n\) 的后缀向从 \(i+1\) 开始的后缀的边权为 \(b_{i+1}-b_i\)（下图中粉色边），是一个非负值。

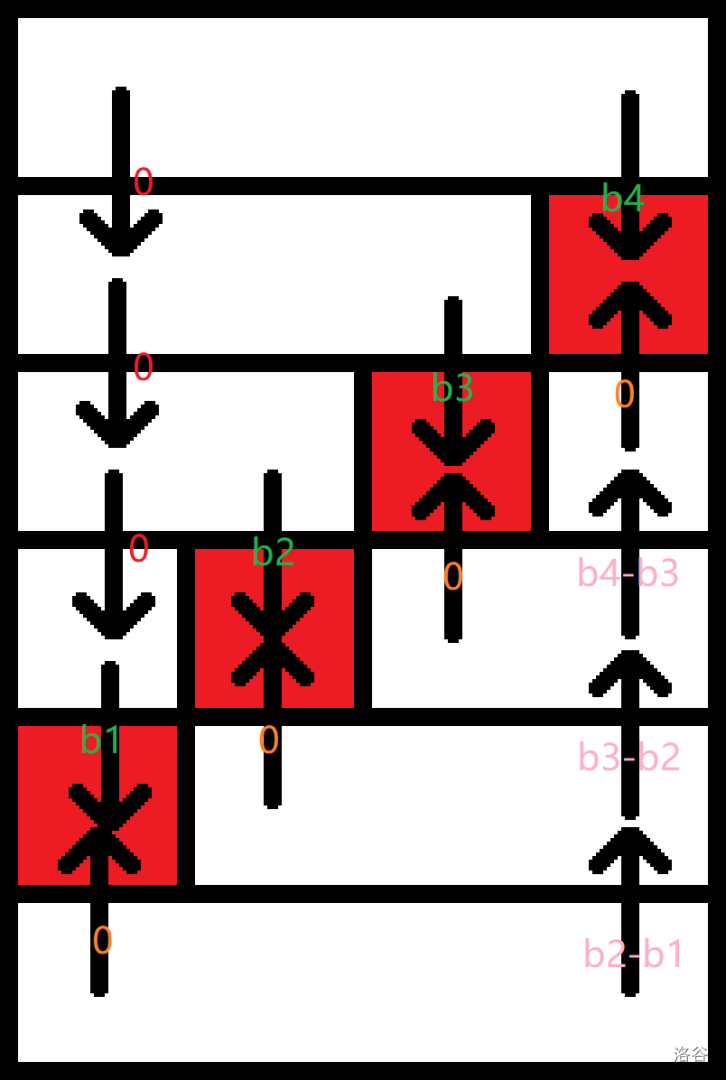
容易发现，此时从 \(u\) 连向后缀 \(r_u\sim n\) 的边权就是 \(a_u+b_{r_u}-m\)。正确性依然显然。

此时，所有边权都是非负的，可以跑 Dijkstra 了！

图的大小为 \(3n\)，边数为 \(6n\) 左右。时间复杂度 \(O(n\log n)\)，空间复杂度 \(O(n)\)。

P10143

不拆贡献，直接考虑一个做出题目编号的集合 \(S\) 被计算多少次。

首先考虑可以做完所有题目的情况答案就是 \(2^n\cdot \sum\limits_{i=1}^na_i\)，所以以下只考虑无法做完所有题目的情况。

分两种情况讨论。下面记 \(\max\limits_{j\in S}j\) 为 \(\max S\)，\(\text{mex }S\) 同理。

• 未完成所有 IOI 赛制题目。

此时，下一个没做完的题 \(i\) 是 IOI 赛制，并且编号 \(>\max S\) 的数 \(i\)。分析得到，只有在 \((i,n]\) 范围内的题目可以任选赛制。证明如下：

1. 所有 \(S\) 内元素必须是 IOI 赛制；
2. \(<\max S\) 且 \(\not\in S\) 的一定是 OI 赛制；
3. \(>\max S\) 且 \(<i\) 的一定是 OI 赛制，\(i\) 一定是 IOI 赛制；
4. \(>i\) 的赛制可以任选。

那么可以决定的赛制数为 \(2^{n-i}\)。同时需要满足无法做完第 \(i\) 道题，即 \(t_i>T-\sum\limits_{j\in S}t_j\)。

那么计算次数就是 \(\sum\limits_{i>\max S}[t_i>T-\sum\limits_{j\in S}t_j]\cdot 2^{n-i}\) 次。

• 完成了所有 IOI 赛制题目。

此时，下一个没做完的题是 OI 赛制。可以得到，这个题一定是 \(\text{mex }S\)。那么同样需要有无法做完这题，即 \(t_{\text{mex }S}>T-\sum\limits_{j\in S}t_j\)；此外，只有 \(<\text{mex }S\) 的可以选定赛制。证明如下：

1. \(<\text{mex }S\) 的赛制可以任选；
2. \(\ge\text{mex }S\) 且 \(\not\in S\) 的必须是 OI 赛制；
3. \(\ge\text{mex }S\) 且 \(\in S\) 的必须是 IOI 赛制。

那么计算次数就是 \([t_{\text{mex }S}>T-\sum\limits_{j\in S}t_j]\cdot 2^{\text{mex }S-1}\) 次。

发现第一个式子只和固定 \(\max S\) 与 \(\sum\limits_{j\in S}t_j\) 可以选出的所有集合 \(S\) 的 \(\sum\limits_{j\in S}a_j\) 和有关，可以 dp；第二个式子只和固定 \(\text{mex } S\) 与 \(\sum\limits_{j\in S}t_j\) 可以选出的所有集合 \(S\) 的 \(\sum\limits_{j\in S}a_j\) 和有关。下面只讨论第一个式子。

可以前缀和优化 dp 算出 \(\max S=a,\sum\limits_{j\in S}t_j=b\) 的集合个数与 \(\sum\limits_{j\in S}a_j\) 之和，然后枚举算贡献。第二个同理。

复杂度 \(O(nT)\)。笔者在考场上被卡常到 1.06s 了，但是没有大力加常数优化。代码公示还没找到，就不放代码了，有兴趣的读者可以自行实现。

CF1503E

考虑一个简单的状压。从右往左扫，然后按列考虑该列黄色的填涂。如果需要是合法的，那么每一行都必然在这三种之内：

1. 黄 - 蓝 - 黄
2. 蓝 - 黄
3. 黄 - 蓝

那么考虑把第一个黄的连续段记作一阶段，出现了蓝的连续段称为二阶段，再一次出现黄称为三阶段，初始都是一阶段。具体转移是：

1. 一阶段时被选中则仍然一阶段，不被选中则进入二阶段；
2. 二阶段时不被选中则仍然二阶段，被选中则进入三阶段；
3. 三阶段必须被选中。

那么容易发现，上面三种每行情况一定是二阶段或者三阶段。可以直接状压转移，复杂度 \(O(3^nn^2m)\)。

下面一阶段省略为 \(1\)，其余同理。

考虑优化。发现三个阶段中，\(3\) 最特殊，因为会限制必须选中。考虑第一次 \(3\) 出现在从右往左扫第 \(t\) 列。那么在第 \(t\) 列前，只能有 \(1\) 与 \(2\)，并且一定形如 若干个 \(2\) - 若干个 \(1\) - 若干个 \(2\)（省略为 \(212\) 形式，下面同理）。考虑分别有 \(a,n-a-c,c\) 个。那么显然前 \(t-1\) 列的选择方案是很好直接算的。考虑第 \(t\) 列的选择。

显然不可以同时碰到上面的 \(2\) 与下面的 \(2\)，因为如果碰到了就会产生 \(313\) 形式的情况，那么后续这段必须全部选中，\(1\) 不可能成为 \(2\) 或 \(3\)，无法产生贡献。那么要么选中的全是一个连续的 \(2\)，要么是一段 \(2\)，一段 \(1\)。

第一种情况，转移到 \(232\) 形式，这个的后续选择方案数是好求的。考虑第二种，会转移到 \(2312\) 或者是 \(2132\) 的形式。\(3\) 相当于分割上下两部分，上面的取后缀，下面的取前缀。上面同样是好算的。仍然考虑 \(1\) 不能被夹在两个 \(3\) 之间，那么一定是先变成 \(32\) 形式再随便转移的。写出式子发现可以转化成一个简单的组合式。

将所有的贡献加起来最终会得到一个式子，简化后如下：

\[\begin{aligned} &2\sum_{t+k=m-2}\sum_{a=0}^{n-1}\binom{a+t}{t}\binom{n-a+t}{t+1}\sum_{i=0}^a\binom{n-i+k}k\binom{i+k}{k+1}\\ -&2\sum_{t+k=m-2}\sum_{a=0}^{n-1}\binom{a+t}t\binom{a+k}{k+1}\binom{n-a+k}k\binom{n-a+t}{t+1}\\ +&2\sum_{t+k=m-2}\sum_{a+c<n}\binom{a+t}t\binom{c+t}t\binom{a+k}{k+1}\binom{2n-2a-c+k}k \end{aligned} \]

前两项都是可以直接 \(O(n^2)\) 求的，考虑后面一项怎么做。记：

\[s=\sum_{t+k=m-2}\sum_{a+c<n}\binom{a+t}t\binom{c+t}t\binom{a+k}{k+1}\binom{2n-2a-c+k}k \]

考虑交换求和号。

\[s=\sum_{a=0}^{n-1}\sum_{t+k=m-2}\binom{a+t}t\binom{a+k}{k+1}\sum_{c=0}^{n-1-a}\binom{c+t}t\binom{2n-2a-c+k}k \]

固定 \(a\)，记

\[f(t,k)=\sum_{c=0}^{n-1-a}\binom{c+t}t\binom{2n-2a-c+k}k \]

那么有

\[\begin{aligned} f(t,k)&=\sum_{c=0}^{n-1-a}\binom{c+t}t\binom{2n-2a-c+k}k\\ &=\sum_{c=0}^{n-1-a}\left(\binom{c+t-1}{t-1}+\binom{c+t-1}t\right)\binom{2n-2a-c+k}k\\ &=f(t-1,k)+\sum_{c=0}^{n-2-a}\binom{c+t}t\binom{2n-2a-c-1+k}k\\ &=f(t-1,k)+\sum_{c=0}^{n-2-a}\binom{c+t}t\binom{2n-2a-c-1+k}k\\ &=f(t-1,k)+\sum_{c=0}^{n-2-a}\binom{c+t}t\left(\binom{2n-2a-c+k}k-\binom{2n-2a-c-1+k}{k-1}\right)\\ &=f(t-1,k)-\binom{n-1-a+t}{t}\binom{n-a+k}{k}+f(t,k)-f(t,k-1)\\ \end{aligned} \]

即

\[\begin{aligned} f(t-1,k)&=f(t,k-1)+\binom{n-1-a+t}{t}\binom{n-a+k}{k}\\ f(t-1,k+1)&=f(t,k)+\binom{n-1-a+t}{t}\binom{n-a+k+1}{k+1} \end{aligned} \]

所以对于每个 \(a\)，可以先 \(O(n)\) 求出 \(f(m-2,0)\)，再 \(O(1)\) 递推出所有 \(f(t,k)\) 的值。

所以，就可以 \(O(n^2)\) 解决这道题目。

P9351

考虑将一个点能花费 \(1\) 的代价到达的区域画出来。下面是 \(n=3\) 的情况。

.#####.
#######
#######
###X###
#######
#######
.#####.

X 是点位置，# 是能到达的点。显然可以拆成四个 \(2n-1\) 边长的正方形。根据经典套路，可以按 \(2n-2\) 为块长分块，将这样一个正方形拆成四个块内前缀和状物。优化建图跑 01BFS 即可。

具体实现细节见代码。常数略大，需要卡常。

P1224

先考虑 \(k=2\) 咋做。

考虑随机出一个集合 \(S\)，找出一个 \(\exists i<j,i,j\in S,2\mid(x_i,x_j)\) 的充分条件，即一个 \(\forall i<j,i,j\in S,2\nmid(x_i,x_j)\) 的必要条件的逆。

如果 \(\forall i<j,i,j\in S,2\nmid(x_i,x_j)\)，那么有 \(\sum\limits_{i<j,i,j\in S}\sum\limits_{k=1}^dx_{i,k}x_{j,k}\equiv\binom{|S|}{2}\pmod{2}\)。但如果只有一组 \((i,j)\) 满足条件，需要跑很多组才能找出来。

所以考虑把所有 \(1\le i\le n\) 随机塞进 \(\sqrt n\) 个桶里面，对于每个桶 \(S\) 以及所有 \(i\)，求出 \(\sum\limits_{j\in S}x_{j,i}\) 与 \(\sum\limits_{j\in S}x_{j,i}^2\)。

然后现对于每个桶 \(S\) 判断，如果 \(\sum\limits_{i<j,i,j\in S}\sum\limits_{k=1}^dx_{i,k}x_{j,k}\not\equiv\binom{|S|}{2}\pmod{2}\)，则桶内暴力枚举 \((i,j)\) 得出答案即可。接下来枚举两个桶 \(S_1,S_2\)，容易合并得出 \(\sum\limits_{j\in S_1\cup S_2}x_{j,i}\) 与 \(\sum\limits_{j\in S_1\cup S_2}x_{j,i}^2\) 的值，就可以得出 \(\sum\limits_{i<j,i,j\in S_1\cup S_2}\sum\limits_{k=1}^dx_{i,k}x_{j,k}\) 的值。如果存在答案，则同样暴力枚举 \((i,j)\) 得出答案。

考虑这样跑 \(O(1)\) 次，就几乎卡不掉了！感受那股劲！那么我们得出了一个 \(k=2\) 时时间复杂度为 \(O(nd)\) 的优秀算法！

然后考虑拓展到 \(k=3\)。对于 \(k=3\)，可以构造充分条件 \(\sum\limits_{i<j,i,j\in S}(\sum\limits_{k=1}^dx_{i,k}x_{j,k})^2\not\equiv\binom{|S|}{2}\pmod{3}\)，如果满足这样条件则 \(S\) 中必然有答案。考虑经典套路之拆贡献，即 \(\sum\limits_{i<j,i,j\in S}(\sum\limits_{k=1}^dx_{i,k}x_{j,k})^2=\sum\limits_{p=1}^d\sum\limits_{q=1}^d\sum\limits_{i<j,i,j\in S}x_{i,p}x_{i,q}x_{j,p}x_{j,q}\)，同样对于每个桶 \(S\) 以及所有 \(p,q\)，求出 \(\sum\limits_{j\in S}x_{j,p}x_{j,q}\) 与 \(\sum\limits_{j\in S}x_{j,p}^2x_{j,q}^2\)，按上面同样的方法做就可以得出答案了。时间复杂度为 \(O(nd^2)\)。

P7803

容易发现，可以把 JOI 三个字母分别看成 \(0,1,2\)，两个数 \(x, y\) 对应的第三个就是 \((-x-y)\bmod 3\)。那么考虑将一个字符串视为一个 \(n\) 维，每维都是 \(\bmod 3\) 意义下的向量，刚开始有 \(S_A,S_B,S_C\) 三个，可以选择两个向量 \(S_1, S_2\) 结合出 \(-S_1-S_2\)。显然组合出的串必然是 \(S_A,S_B,S_C\) 的线性组合，设为 \(aS_A+bS_B+cS_C\)，可以发现当且仅当 \(a+b+c\equiv 1\pmod 3\) 时能够构造出来。因此能构造出的串只有 \(9\) 种，先暴力求出。

然后考虑如何匹配。可以哈希，但是容易被卡而且很麻烦！来一个确定性做法。题目中给定的操作只有颜色段赋值，那么只要能够实现每次操作时间复杂度和减去的颜色段数相同即可。考虑对于 \(9\) 个串分别维护当前询问串与其相同位置数，修改时对于跨过的段删除贡献，加入一整段时再加上即可。最终时间复杂度 \(O(9n+n\log n)\)。

P5298

考虑 dp，设 \(f_{u,i}\) 为 \(u\) 节点权值 \(\le i\) 的概率。那么有

\[f_{u,i}=p_u\prod_{v\in \text{son}_u}f_{v,i}+(1-p_u)\left(1-\prod_{v\in \text{son}_u}(1-f_{v,i})\right) \]

暴力合并是直接将 \(\prod\limits_{v\in \text{son}_u}f_{v,i}\) 和 \(\prod\limits_{v\in \text{son}_u}(1-f_{v,i})\) 求出来，从而计算。现在要对于多个 \(i\) 同时做，那么使用一个行向量 \(\begin{bmatrix}1&1\end{bmatrix}\)，然后将所有 \(v\in\text{son}_u\) 的 \(f_{v,i}\) 贡献到第一个，\(1-f_{v,i}\) 贡献到第二个。然后接下来假设得到的矩阵是 \(\begin{bmatrix}a&b\end{bmatrix}\)，还需要变换成 \(\begin{bmatrix}p_ua+(p_u-1)b+1-p_u&-p_ua+(1-p_u)b+p_u\end{bmatrix}\)。

这并不是一个线性变换，所以考虑在向量后面再加一个 \(1\)，则解决 \(u\) 子树（即用数据结构维护出 \(V_{u,i}=\begin{bmatrix}f_{u,i}&1-f_{u,i}&1\end{bmatrix}\)）过程变成：

1. 对于 \(v\in\text{son}_u\) 解决问题；
2. 初始化所有 \(V_{u,i}=\begin{bmatrix}1&1&1\end{bmatrix}\)；
3. 合并所有的 \(v\in\text{son}_u\) 的答案进入 \(u\) 所维护的数据结构（对应位置乘）；
4. 将所有位置的向量右乘一个矩阵：

\[\begin{bmatrix} p_u&-p_u&0\\ p_u-1&1-p_u&0\\ 1-p_u&p_u&1 \end{bmatrix}\]

考虑对于 \(V_{u,i}\) 维护一颗带有懒标记的动态开点线段数（实际上只需要每个点维护一个懒标记），然后进行线段树合并，发现如果递归到一个节点时，合并的两颗树其中的一颗这个节点叶子节点，那么只需要将另一颗树对应节点标记乘上一个新矩阵即可。

最终时间复杂度瓶颈是标记的下传，每次下传复杂度是 \(O(3^3)\)，下传 \(O(n\log n)\) 次（离散化后复杂度），最终时间复杂度为 \(O(27n\log n)\)。空间复杂度是 \(O(9n\log n)\)，瓶颈也是每个节点存一个矩阵作为标记。

CF1572D

首先给定的图是二分图，转成二分图最大权匹配。但是如果把边权放在中间的边上会比较困难，那么把边权放在两边。建图是这样的：

• 源点向二进制位为 \(1\) 个数为偶数的 \(i\) 连费用为 \(a_i\) 的，容量为 \(1\) 的边。
• 二进制位为 \(1\) 个数为偶数的 \(i\) 向原图中相邻的点连费用为 \(0\)，容量为 \(+\infty\) 的边。
• 二进制位为 \(1\) 个数为奇数的 \(i\) 向汇点连费用为 \(a_i\)，容量为 \(1\) 的边。

答案就是这个流量 \(\le k\) 的最大费用流费用。

新增加一条增广流时必然是这两种情况之一：

• 从源点流向左部，再通过一条正向边流向右部，再流向汇点。
• 从源点流向左部，再通过正向边流向右部，再走反向边回左部，再走正向边到右部，经过若干次这样走反向再走正向的过程，最后从右部点流出。

此时边权放在两边的好处体现了：在这样的过程中只有第一条边和最后一条边会产生费用。

由于将中间正向边容量设为了 \(+\infty\)，所以可以看作一直存在。那么考虑目前流量为 \(f\) 时怎么增广。此时中间必然有 \(f\) 条反向边。上述的第一种是比较平凡的，考虑第二种，可以把反向边看作点，两个反向边可以通过一个正向边连接起来就连边（注意这里是有向边），然后跑传递闭包就可以知道是否存在一种方案走第一条反向边是 \(i\) 最后一条是 \(j\)。对于 \(i\) 找到最大权的可以流向 \(i\) 起点的左部点，\(j\) 找到最大权的可以从 \(j\) 流向起点的右部点，可以算出对应增广的费用。找到最优的即可。这部分只需要存一下反向边就可以维护了。

接下来问题是在流满一条从源点到左部点的边与一条从右部点到汇点的边时怎么更新信息。此时可以直接重构相关的点的信息，复杂度 \(O(n^2)\)。

那么最终总复杂度就是 \(O(\frac{k^4}\omega+2^nn+n^2k)\)，能够通过。

CF1849F

考虑二分，答案可以 \(\ge x\) 等价于 \(V=\{1,\cdots,n\},E=\{(u,v)\mid u\ne v,a_u\oplus a_v<x\}\) 的图为二分图。建出 01-Trie，数位 dp，则对于一个 \(u\)，满足 \(a_u\oplus a_v<x\) 的 \(a_v\) 是 \(\le \log V\) 个子树构成的集合。但是还需要把 \(u\) 剥掉，集合还是若干个子树。

那就相当于需要处理若干组一个节点与一个 01-Trie 上子树内所有叶子节点异色的要求，最后求是否有解。直接对于每个节点记录其子树是否已经钦定全部染同一个颜色，在钦定一个节点和一个子树内所有元素内异色时，如果这个子树已经被钦定染一个颜色，就只需要并查集上钦定这个节点与子树内一个节点异色；如果还没有，就暴力钦定这个节点与子树内所有节点异色，此时就可以记录这个子树全部同色。这样每个子树只会暴力一次，一个叶子只出现在 \(1+\log V\) 个子树内，只需要 \(O(n\log V)\) 次并查集操作。只需要 check 一次的情况下可以直接 dfs 判断二分图，此时复杂度为 \(O(n\alpha(n)\log^2 V)\)，常数略大但应该还是能过。

但是其实发现可以直接把二分丢掉，改成逐位确定是否可以是 \(1\)，每次用带权并查集处理新多出来的数位 dp 要求，如果矛盾了就回滚操作（因此不能路径压缩），最终时间复杂度为 \(O(n\log V\log n)\)，并且瓶颈是并查集的小常数，可以在 1s 内通过。

AT_arc130_d

首先把这个树黑白染色，设黑点集合为 \(S\)，答案为所有黑点往白点连边后形成的 DAG 的拓扑序计数的两倍，但是任意 DAG 拓扑序计数目前没有多项式复杂度做法。

接下来，不妨设树是一颗有根树，那么对于儿子指向父亲的边容斥变为父亲指向儿子的边，父亲指向儿子的边直接保留，就转化成了一个森林的拓扑序计数，答案为 \(\frac{n!}{\prod\limits_{u=1}^n|T_u|}\)，其中 \(T_u\) 是只保留父亲指向儿子的边与反向的儿子指向父亲的边后 \(u\) 的子树。

在这个容斥的基础上改成树上背包的形式：\(f_{u,i}\) 表示以 \(u\) 为根的子树，只保留父亲指向儿子的边与反向的儿子指向父亲的边后 \(u\) 的子树大小为 \(i\) 的所有方案的 \((-1)^k{\prod\limits_{u}^n|T|}\)，其中 \(k\) 为钦定反向边的条数。那么答案为 \(2n!\sum\limits_{i=1}^nf_{u,i}\)，转移式为：

\[f_{u,i}= \begin{aligned}\begin{cases} \frac1i\times\left(\prod\limits_{v\in son_u}\left(\sum\limits_{j=1}^{sz_v}f_{v,j}z^j\right)\right)[z^{i-1}]&,u\in S\\ \frac1i\times\left(\prod\limits_{v\in son_u}\left(\sum\limits_{j=1}^{sz_v}f_{v,j}-\sum\limits_{j=1}^{sz_v}f_{v,j}z^j\right)\right)[z^{i-1}]&,u\notin S \end{cases} \end{aligned} \]

其中 \(1\le i\le sz_u\)。

那么树形背包实现即可，时空复杂度为 \(O(n^2)\)。

P4547

考虑先钦定一个完美匹配 \(i\rightarrow p_i\)，那么如果里面有 \(c_1\) 组第一种边对中两条边同时出现（即第一类边对 \((u_1\rightarrow v_1,u_2\rightarrow v_2)\) 中满足 \(v_1=p_{u_1}\land v_2=p_{v_2}\)的数量），\(c_2\) 组第二种边对中两条边同时出现，那么这个匹配对答案的贡献为 \(2^{-n}\cdot 2^{c_1}\cdot 0^{c_2}\)。将恰好转成钦定，那么根据二项式定理，先钦定 \(c_1\) 组第一种边对中两条边同时出现，钦定 \(c_2\) 组第二种边对中两条边同时出现，然后再钦定剩余的匹配，这样的方案每个贡献为 \(2^{-n}\cdot 1^{c_1}\cdot (-1)^{c_2}\)。

那么直接考虑状压 dp，\(f_{S,T}\) 代表左部点还有 \(S\) 集合没有钦定，右部点还有 \(T\) 集合没有钦定的所有方案贡献和。接下来分三种转移：

• 钦定一个匹配。\(f_{S,T}\leftarrow f_{S\backslash u,T\backslash v}\)，要求 \(u\rightarrow v\) 有可能出现即可。
• 钦定两个匹配。\(f_{S,T}\leftarrow f_{S\backslash u_1\backslash u_2,T\backslash v_1\backslash v_2}\)，要求这两个匹配为第一种关系。
• 钦定两个匹配。\(f_{S,T}\leftarrow -f_{S\backslash u_1\backslash u_2,T\backslash v_1\backslash v_2}\)，要求这两个匹配为第二种关系。

由于上面的钦定为无序的，所以上述转移中 \(u\) 与 \(u_1\) 直接选择 \(S\) 中最小的元素即可不计算重复。

这样状态数是 \(O(\binom{2n}n)\)，每个状态转移数 \(O(n)\)，复杂度 \(O(\binom{2n}nn)\)。滚动数组实现即可不爆空间，但发现时间无法通过怎么办？

其实很简单，直接把上面正向转移改成反向转移，每次只对于 \(f_{S,T}\) 有非零值的转移，就可以通过了。

CF833B k 无关

首先要做 \(k\) 无关，第一步肯定是直接上一个 wqs 二分，把题目转成区间贡献是颜色数再加上一个常数 \(C\)，那还是满足四边形不等式，然后区间个数的限制就成功去掉了。

然后接下来发现成功将问题从一个分层离线转移变成了一层半在线转移。这个时候上二分队列，但是发现完全无法快速对于区间代价随机查询。考虑将随机查询改成移动左右端点指针的方法，但是这个方法要求离线，那这个时候套用半在线卷积的做法，上一个 CDQ 分治。

然后接下来发现成功将问题从一层半在线转移转成了一层全局离线转移，具体地就是，如果已经知道了 \(f_l\) 到 \(f_m\)，对于所有 \(i\in[m+1,r]\) 找到 \(j\in[l,m]\) 使得 \(f_j+w(j+1,i)\) 最大，此时仍然满足决策单调性，再套用经典的分治指针移动的套路，此时指针移动次数是 \(O((r-l)\log n)\) 的。

最终通过嵌套套路，我们得到了一个复杂度为 \(O(n\log^3n)\) 的优秀做法！但是我还没有写。

更加有趣的是，对于“区间代价满足四边形不等式求区间拆分代价最值，只允许移动左右端点指针不允许随机查询”这一类问题，套用这样的做法不仅可以得到指针移动次数 \(O(n\log^2n)\) 的复杂度，甚至可以求两边最值：满足反四边形不等式的区间代价，经过 CDQ 分治一步，决策也变成了单调的，因此也可以直接套用分治做法。

upd：发现静态区间颜色数确实是可以在线随机查询的，但是稍微改改就不行了！

P11817

考虑拆出两条边的顺序，把每个点 \(u\) 拆成 \(i_{u,1/2},o_{u,1/2}\)，代表入和出的第一、二条边，每条边 \((u,v)\) 相当于匹配了 \(o_{u,i}\) 与 \(i_{v,j}\)，那么这样每个合法方案会变成 \(4^n\) 个方案，需要除掉。问题转化为一个二分图，左部为 \(o_{u,1/2}\)，右部为 \(i_{u,1/2}\)，满足：

1. 对于任何 \(u\) 不允许匹配 \(o_{u,1/2}\) 和 \(i_{u,1/2}\)；（不能有自环）
2. 对于任何一对 \((u,v)\) 不允许 \(o_{u,1/2}\) 和 \(i_{u,1/2}\) 匹配两条边。（不能有重边）

先不考虑限制 2，只考虑限制 1。直接容斥，选定有 \(a\) 个 \(u\) 的 \(o_{u,1/2}\) 和 \(i_{u,1/2}\) 之间连了 \(1\) 条边，\(b\) 个连了 \(2\) 条。所以答案就是 \(\sum\limits_{a+b\le n}4^a2^b(-1)^{a+2b}\frac{n!}{a!b!(n-a-b)!}(2n-a-2b)!\)。

然后考虑限制 2。同样容斥，选定若干组 \(o_{u,1/2}\) 与 \(i_{v,1/2}\) 匹配后会有四类点 \(u\)：

1. \(o_{u,1/2}\) 与 \(i_{u,1/2}\) 都没有匹配的点；
2. \(o_{u,1/2}\) 与 \(i_{u,1/2}\) 都匹配了的点；
3. 匹配了 \(i_{u,1/2}\)，未匹配 \(o_{u,1/2}\) 的点；
4. 匹配了 \(u_{u,1/2}\)，未匹配 \(i_{u,1/2}\) 的点；

2 类点没有影响，并且 3、4 类点个数相同。假设 1 类点个数为 \(x\)，3、4 类点个数为 \(y\)，那么剩余的满足限制 1 的方案数同样可以容斥，答案为 \(\sum\limits_{a+b\le x}4^a2^b(-1)^{a+2b}\frac{x!}{a!b!(n-a-b)!}(2x+2y-a-2b)!\)。设这个值是 \(f(x,y)\)，通过朴素枚举可以 \(O(n^4)\) 求出所有 \(f(x,y)\)。

假设选定连边是有顺序的，那么如果目前 1 类点个数为 \(x\)，3、4 类点个数为 \(y\)，接下来新的连边可能有如下几种情况：

• 选择两个不同的一类点 \(u, v\) 匹配 \(o_u\) 与 \(i_v\)，\(x\leftarrow x-2,y\leftarrow y+1\)，方案数为 \(x^2-x\)；（\(x\ge2\)）
• 选择一个三类点 \(u\) 与一个四类点 \(v\)，匹配 \(o_u\) 与 \(i_v\)，\(y\leftarrow y-1\)，方案数为 \(y^2\)；（\(y\ge1\)）
• 选择一个一类点 \(u\) 与一个四类点 \(v\)，匹配 \(o_u\) 与 \(i_v\)，\(x\leftarrow x-1\)，方案数为 \(xy\)；（\(x,y\ge1\)）
• 选择一个三类点 \(u\) 与一个一类点 \(v\)，匹配 \(o_u\) 与 \(i_v\)，\(x\leftarrow x-1\)，方案数为 \(xy\)；（\(x,y\ge1\)）

需要注意，此时不能取一类点 \(u\) 匹配 \(o_u\) 与 \(i_u\)，因为这样会使后续无自环的容斥出错。

因此考虑 dp，\(dp_{x,y}\) 代表有序地选定若干条边后，1 类点个数为 \(x\)，3、4 类点个数为 \(y\)，选定边的方案数。初值是 \(dp_{n,0}=1\)，转移直接按上述的几个情况转移即可。

统计答案时，由于上述 dp 为了转移方便选定了边之间顺序，所以需要除一个阶乘取消影响，因此答案就是 \(\sum\limits_{x+y\le n}\frac{dp_{x,y}}{(n-x-y)!}(-2)^{n-x-y}f(x,y)\)。

目前复杂度是 \(O(n^4)\) 的，除了求 \(f(x,y)\) 的部分别的地方复杂度只有 \(O(n^2)\)，考虑怎么优化求 \(f(x,y)=\sum\limits_{a+b\le x}4^a2^b(-1)^{a+2b}\frac{x!}{a!b!(n-a-b)!}(2x+2y-a-2b)!\) 值的复杂度。观察到最后一个阶乘项不方便处理，直接把 \(a+2b\) 拆出去：设 \(F(z)=\sum\limits_{a+b\le x}(-4z)^a(2z^2)^b\frac{x!}{a!b!(n-a-b)!}=(2z^2-4z+1)^x\)，则 \(f(x,y)=\sum\limits_{0\le p\le 2x}F[z^p](2x+2y-p)!\)。而 \(F\) 只和 \(x\) 有关，所以对于 \(x\) 从小到大求出 \(F\)，根据 \(F\) 算出所有 \(f(x,y)\) 就可以做到 \(O(n^3)\) 了。

本来打算直接贴代码了，但是想了想，能不能再牛一点？发现 \(f(x,y)=\left((2z^2-4z+1)^x\left(\sum\limits_{i\ge 0}i!z^i\right)\right)[z^{2x+2y}]\)，本来想这里可以直接上一个 MTT，但是其实发现直接维护 \((2z^2-4z+1)^x\left(\sum\limits_{i\ge 0}i!z^i\right)\)，每次 \(x\) 增加 \(1\) 就乘上 \(2z^2-4z+1\)，复杂度就做到 \(O(n^2)\) 了！！！！

P10218

先考虑一个 \(O(n\cdot\text{poly}(k))\) 的做法。考虑二分，由于 \(a_i+x\ge a_i\oplus x\)，答案可以 \(\ge B\) 的充要条件是存在 \(x\in[0,2^k)\)，使得 \(\min a_i+x\ge B\) 且 \(\sum\limits_{i=1}^n[a_i\oplus x< B]b_i\le m\)。

这个时候可以直接维护，算出满足 \(\sum\limits_{i=1}^n[a_i\oplus x< B]b_i\le m\) 的 \(x\) 的最大值 \(x'\)，判断一下是否有 \(x'\ge B-\min a_i\) 即可。问题的关键变为如何求出 \(x'\)。

可以考虑对于每个 \(i\)，把满足 \(a_i\oplus x< B\) 的 \(x\) 加上 \(b_i\)，这容易让人联想到数位 dp，使用数位 dp 与 01-Trie 将这样的 \(x\) 拆成 \(O(k)\) 个子树，相当于在这几个子树的根上打一个 \(+b_i\) 的标记，那么对于一个 \(x\)，\(\sum\limits_{i=1}^n[a_i\oplus x< B]b_i\) 的值就是其根链上标记的和，共有 \(O(nk)\) 个标记。假设 01-Trie 是满的，那么整个 01-Trie 上的叶子可以分为 \(O(nk)\) 个子树，每个子树内叶子 \(x\) 的
\(\sum\limits_{i=1}^n[a_i\oplus x< B]b_i\) 值全部相同。那么可以做到 \(O(nk^2)\) 的复杂度。

后面就是比较意识流的一步了……回想数位 dp 的过程，我们是如何把 \(x\oplus A<B\) 的所有 \(x\) 分成 \(k\) 个子树的：对于第 \(i\) 位，若 \(B\) 的二进制的第 \(i\) 位为 \(1\)，则对于所有满足下列条件的 \(x\) 会有 \(x\oplus A<B\)：

• \(x\) 高于 \(i\) 的位全部与 \(A\oplus B\) 相同；
• \(x\) 的第 \(i\) 位为 \(A\) 的第 \(i\) 位。

并且这样不会重复。还是有点抽象，再往 01-Trie 方向想一下：相当于 01-Trie 上 \(A\oplus B\) 的根链上，对于 \(B\) 的第 \(i\) 位，若这一位不是 \(0\)，那么 \(A\oplus B\) 在这一层上的祖先的兄弟需要打一个标记。

考虑逐位确定 \(B\)，如果现在在试图确定 \(B\) 的第 \(i\) 位，那么总共有这样的 \(n\) 条根链，目前延伸到第 \(i\) 层，并且已经打了一些标记，想要确定在假设 \(B\) 的第 \(i\) 位是 \(1\) 情况下的 \(x'\) 值是多少。

在假设 \(B\) 的第 \(i\) 位是 \(1\) 时，会新增 \(n\) 个同一层的标记，并且每个根链会向指定方向多延伸一段。此时直接求出 \(x'\) 是相当困难的，可以利用以前的信息。

注意到在确定完之前的位后，以后所有标记只有可能出现在所有根链延伸到的 \(O(n)\) 个点的子树内，其他的同层子树内不会再打标记了，也就是说除了这 \(O(n)\) 个点以外，剩下的同层的点的子树内部的 \(\sum\limits_{i=1}^n[a_i\oplus x< B]b_i\) 值已经确定不可能再改变了，可以把其中的 \(\le m\) 的部分直接贡献到一个“不重要部分”的答案里面，记为 \(x_d\)。对于剩下的 \(O(n)\) 个点，暴力 \(O(n)\) 求出内部的 \(x_a\)，则 \(x'=\max\{x_d,x_a\}\)。

在向下走一层的时候，一些点会失去部分子树，把这些子树内最大的点贡献到 \(x_d\) 里面。最终复杂度就只有 \(O(nk)\)，代码也没什么细节。