AI可解释性 I | 对抗样本(Adversarial Sample)论文导读(持续更新)
导言
本文作为AI可解释性系列的第一部分,旨在以汉语整理并阅读对抗攻击(Adversarial Attack)相关的论文,并持续更新。与此同时,AI可解释性系列的第二部分:归因方法(Attribution)也即将上线,敬请期待。
Intriguing properties of neural networks(Dec 2013)
作者:Christian Szegedy
简介
Intriguing properties of neural networks 乃是对抗攻击的开山之作,首次发现并将对抗样本命名为Adversarial Sample,首先发现了神经网络存在的两个性质:
-
单个高层神经元和多个高层神经元的线性组合之间并无差别,即表示语义信息的是高层神经元的空间而非某个具体的神经元
there is no distinction between individual high level units and random linear combinations of high level units, ..., it is the space, rather than the individual units, that contains of the semantic information in the high layers of neural networks.
-
神经网络的输入-输出之间的映射很大程度是不连续的,可以通过对样本施加难以觉察的噪声扰动(perturbation)最大化网络预测误差以使得网络错误分类,并且可以证明这种扰动并不是一种随机的学习走样(random artifact of learning),可以应用在不同数据集训练的不同结构的神经网络
we find that deep neural networks learn input-output mappings that are fairly discontinuous to a significant extend. Specifically, we find that we can cause the network to misclassify an image by applying a certain imperceptible perturbation, which is found by maximizing the network's prediction error. In addition, the specific nature of these perturbations is not a random artifact of learning: the same perturbation can cause a different network, that was trained on a different subset of the dataset, to misclassify the same input.
神经元激活
文章通过实验证明,某个神经元的方向(natural basis direction)和随机挑选一个方向(random basis)再和整个层级的激活值作余弦相似度之后的结果完全不可区分。
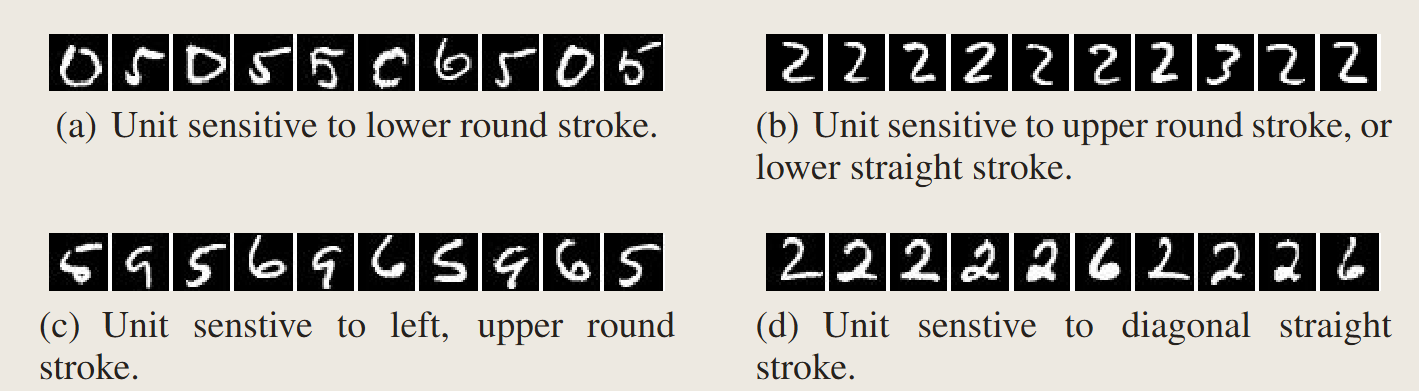
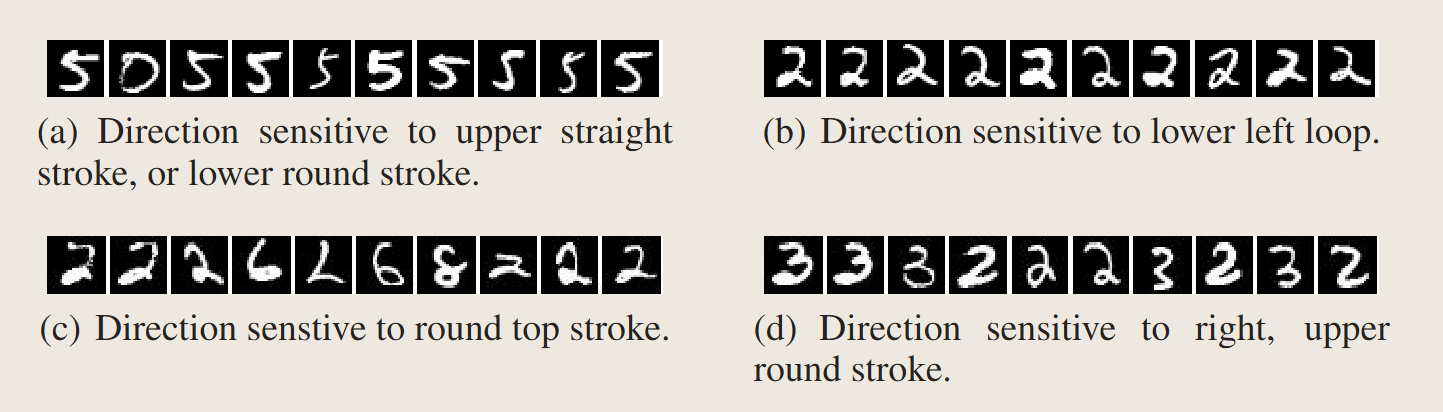
可以证明,单个神经元的解释程度和整个层级的解释程度不分伯仲,即所谓”神经网络解耦了不同坐标上的特征“存在疑问。
This suggest that the natural basis is not better than a random basis in for inspecting the properties of \(\phi(x)\). Moreover, it puts into question the notion that neural networks disentangle variation factors across coordinates.
虽然每个层级似乎在了输入分布的某个部分存在不变性,但是很明显在这些部分的邻域中又存在着一种反直觉的未定义的行为。
神经网络的盲点(Blind Spots in Neural Networks)
观点认为神经网络的多层非线性叠加的目的就是为了使得模型对样本空间进行非局部泛化先验(non-local generalization prior)的编码,换句话说,输出可能会对其周围没有训练样本的输入空间邻域分配不显著(推测约为非\(\epsilon\))的概率(对抗攻击可以发生的假设)。这样做的好处在于,不同视角的同一张图片可能在像素空间产生变化,但是经过非局部泛化先验编码使得在概率上的输出是不变的。
In other words, it is possible for the output unit to assign non-significant (and, presumably, non-epsilon) probabilities to regions of the input space that contain no training examples in their vicinity.
这里可以推导出一种平滑性假设,即训练样本在\(\epsilon\)领域内(\(||x^\prime-x||<\epsilon\))的所有样本都是满足和训练样本的类别一致。
And that in particular, for a small enough radius " in the vicinity of a given training input x, an x " which satisfies ||x x " || < " will get assigned a high probability of the correct class by the model.
Uzuki评论:神经网络验证做的工作就是寻找这个\(\epsilon\),证明在\(\epsilon\)邻域内不存在对抗样本
接下来,作者将通过实验证明这种平滑性假设在很多的核方法(kernel method)上都是不成立的,可以通过一种高效的优化算法完成(即对抗攻击),这种优化过程在于遍历从网络形成的流形上以寻找“对抗样本”。这些样本在网络的高维流形上被认为是低概率出现的局部“口袋“。
In some sense, what we describe is a way to traverse the manifold represented by the network in an efficient way (by optimization) and finding adversarial examples in the input space.
算法的形式化描述
给定一个分类器\(f:\mathbb{R}^m\rightarrow \{1\dots k\}\)以及一个连续的损失函数\(\mathbb{R}^m\times\{1\dots k\} \rightarrow \mathbb{R}^+\),输入图像\(x\in\mathbb{R}^m\)和目标类别${1\dots k} $以解开下面如下的箱约束(box-constrained)问题:
- 最小化\(||r||_2\)并保证:
- \(f(x+r)=l\)
- \(x+r\in[0,1]^m\)(确保是RGB范围)
这个问题只要\(f(x)\neq l\)就是一个非平凡的难解问题,因此我们通过box-constrained L-BFGS算法去优化近似求解。问题可以如下表示:通过线搜索找到一个最小的\(c\),以最小化\(r\)
- 最小化\(c|r|+\text{loss}_f(x+r,l)\quad s.t.\quad x+r\in[0,1]^m\)
In general, the exact computation of D(x, l) is a hard problem, so we approximate it by using a box-constrained L-BFGS. Concretely, we find an approximation of D(x, l) by performing line-search to find the minimum c > 0 for which the minimizer r of the following problem satisfies f (x + r) = l.
实验
通过实验,可以得到如下三个结论:
- 对于文章研究的所有网络(包括MNIST、QuocNet、AlexNet),针对每个样本,始终能够生成与原始样本极其相似、视觉上无法区分的对抗样本,且这些样本均被原网络误分类。
- 跨模型的泛化性:当使用不同超参数(如层数、正则化项或初始权重)从头训练网络时,仍有相当比例的对抗样本会被误分类。
- 跨训练集的泛化性:在完全不同的训练集上从头训练的网络,同样会误分类相当数量的对抗样本。
- For all the networks we studied (MNIST, QuocNet [10], AlexNet [9]), for each sample, we always manage to generate very close, visually indistinguishable, adversarial examples that are misclassified by the original network (see figure 5 for examples).
- Cross model generalization: a relatively large fraction of examples will be misclassified by networks trained from scratch with different hyper-parameters (number of layers, regularization or initial weights).
- Cross training-set generalization a relatively large fraction of examples will be misclassified by networks trained from scratch trained on a disjoint training set.
可以证明对抗样本存在普适性,一个微妙但关键的细节是:对抗样本需针对每一层的输出生成,并用于训练该层之上的所有层级。实验表明,高层生成的对抗样本比输入层或低层生成的更具训练价值。
A subtle, but essential detail is that adversarial examples are generated for each layer output and are used to train all the layers above. Adversarial examples for the higher layers seem to be more useful than those on the input or lower layers.
然而,这个实验仍然留下了关于训练集依赖性的问题。生成示例的难度是否仅仅依赖于我们训练集作为样本的特定选择,还是这一效应能够泛化到在完全不同训练集上训练的模型?
Still, this experiment leaves open the question of dependence over the training set. Does the hardness of the generated examples rely solely on the particular choice of our training set as a sample or does this effect generalize even to models trained on completely different training sets?
网络不稳定性的谱分析
作者将上一节提出这种监督学习网络对这些特定的扰动族存在的不稳定性可以被如下数学表示:
给定多个集合对\((x_i,n_i)\),使得\(||n_i||<\delta\)但\(||\phi(x_i;W)-\phi(x_i+n_i;W)||\ge M \ge 0\),其中\(\delta\)是一个非常小的值,\(W\)是一个一般的可训练参数。那么这个不稳定的扰动\(n_i\)取决于网络结构\(\phi\)而非特定训练的参数\(W\)
Uzuki评论:这个结论就不得不提对抗训练(Adversarial training)了,因为对抗训练不改变网络结构但是改变了训练集的结构以生成不同的训练参数,提高模型对对抗样本的防护能力,因此对抗训练应该是证明了某个特定的对抗样本生成算法本身总不是最优的
结论
通过寻找对抗样本的过程,我们可以证明神经网络本身并没有很好地实现泛化能力,尽管这些对抗样本在训练过程中出现的概率是极低的,但是模型构建的空间本身是稠密的,几乎每个正常样本都能寻找到对抗样本。