本文作者:\(\color{red}\text{DoubleQLzn}\color{green}✓\)
题目:洛谷 P1126 机器人搬重物 - 题目传送门
难度:\(\color{green}\tt 普及+\)
\(\text{Knowledge}\)
- 【\(5\)】广度优先搜索
- 【\(3\)】队列
- 【\(3\)】结构体
\(\text{Solution}\)
本题一有 \(5\) 种操作,其中方向影响我们的移动。
如果我们直接对点进行操作,无法得到移动的方向。因此,我们考虑拆点。
本来的状态为 \((i,j)\),表示机器人以第 \(i\) 行第 \(j\) 列为左上角。我们考虑加上方向一维,状态为 \((i,j,d)\)。
为了方便左转与右转:
- 东:\(d=0\)
- 南:\(d=1\)
- 西:\(d=2\)
- 北:\(d=3\)
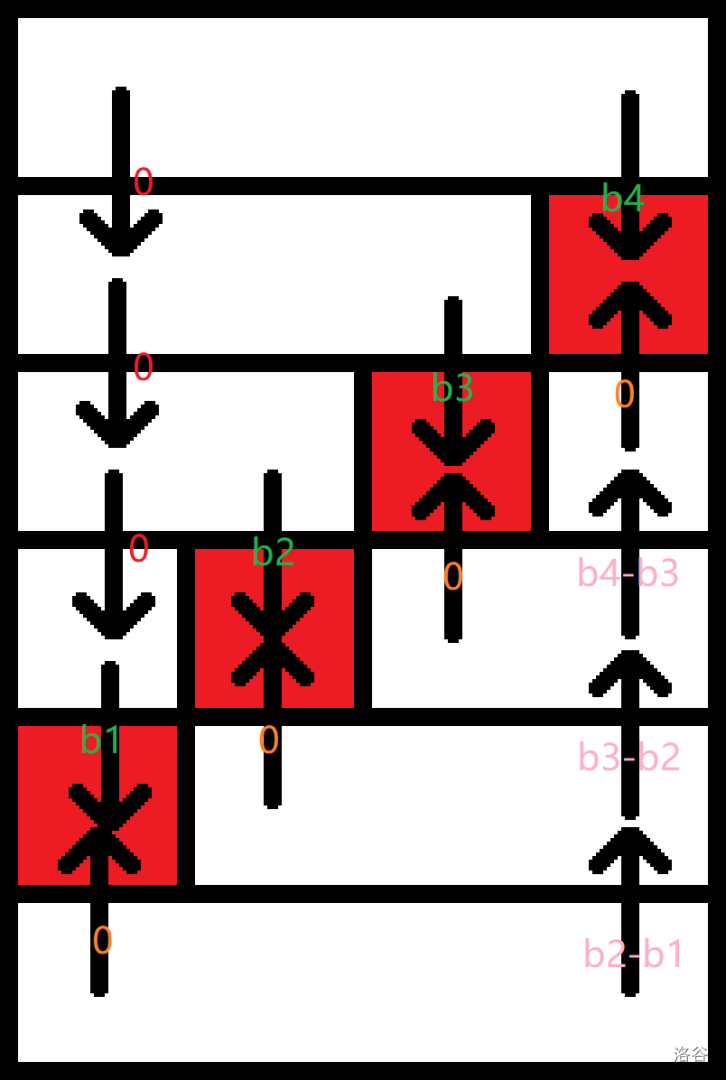
因此 \((d+3)\bmod 4\) 与 \((d+1)\bmod 4\) 即为左转与右转。最后用状态广度优先搜索即可。在向前时,用原本的方向数组乘 \(1,2,3\) 即可。
下面来讲讲这道题的坑点:
- 机器人不能穿墙,如果走 \(1\) 步有墙,后面的都不行。
- 机器人直径是 \(1.6\) 米。
- 若 \((i,j)\) 为障碍,则 \((i-1/i,j-1/j)\) 也是障碍。
- 因为是左上角,最后一行与最后一列不能经过。
\(\text{Code}\)
#include <bits/stdc++.h>
using namespace std;
int n,m,a[105][105],step[105][105][4],sx,sy,ex,ey;
char dir;
int dx[4] = {0,1,0,-1};
int dy[4] = {1,0,-1,0};
struct Node
{int x,y,d;
};
void bfs(int x,int y,int d)
{queue<Node> q;q.push({x,y,d});step[x][y][d] = 0;while (!q.empty()){Node t = q.front();q.pop();x = t.x,y = t.y,d = t.d;if (x == ex && y == ey){cout << (step[ex][ey][d]);return;}int nd = (d + 1) % 4;if (!step[x][y][nd]){step[x][y][nd] = step[x][y][d] + 1;q.push({x,y,nd});}nd = (d + 3) % 4;if (!step[x][y][nd]){step[x][y][nd] = step[x][y][d] + 1;q.push({x,y,nd});}for (int i = 1;i <= 3;i++){int nx = x + dx[d] * i,ny = y + dy[d] * i;if (nx >= 1 && nx < n && ny >= 1 && ny < m && a[nx][ny] == 0){if (!step[nx][ny][d]){step[nx][ny][d] = step[x][y][d] + 1;q.push({nx,ny,d});}} else break;}}cout << -1;
}
int main()
{cin >> n >> m;for (int i = 1;i <= n;i++){for (int j = 1;j <= m;j++){int t;cin >> t;if (t == 1){a[i][j] = 1;a[i - 1][j] = 1;a[i][j - 1] = 1;a[i - 1][j - 1] = 1;}}}cin >> sx >> sy >> ex >> ey >> dir;int d = 0;if (dir == 'S') d = 1;if (dir == 'W') d = 2;if (dir == 'N') d = 3;bfs(sx,sy,d);return 0;
}