std 怎么根号的,来点 poly log 做法
首先直接二分答案,设当前二分的值为 \(K\):
令 \(c_i\) 为有在 \(l\sim i\) 满足条件的时候最多有多少个 \(i\) 变成了 \(i+1\),则有递推式
如果 \(c_{L-1}\sim c_R\) 有一个 \(<0\) 就不合法,否则合法。
观察递推式,上面的限制可以直接抽象成
对于所有 \(L-1\le l\le r\le R\) 均满足 \(\displaystyle (r-l)K\le \sum_{i=l}^r b_i+\sum_{i=l+1}^r a_i\),也就是
区间的子区间维护不可加减信息看着非常蛋疼,直接对着右面的东西分治,拼合左右两边可以抽象成下面的问题:
给定 \(L,R\) 数组,检验下面的东西是否 \(\ge 0\):
好消息是两边独立了,可以拿李超树维护两个东西的 \(\min\),多组询问就是分治的时候对两边维护可持久化李超树,询问的时候直接二分 \(K\) 可以做到 \(\log^3\) 的时间复杂度
但是这个玩意因为复杂度太大死翘翘了,必须得去点 \(\log\)
分治的时候问 \(\log\) 次非常浪费,注意到除了一组询问外每组询问都是 \([l',r]\) 或者 \([l,r']\) 的形式,其中 \(l\) 和 \(r\) 是当前分治区间的左右端点,可以把这些玩意一口气预处理出来,每次就可以 \(O(1)\) 查了
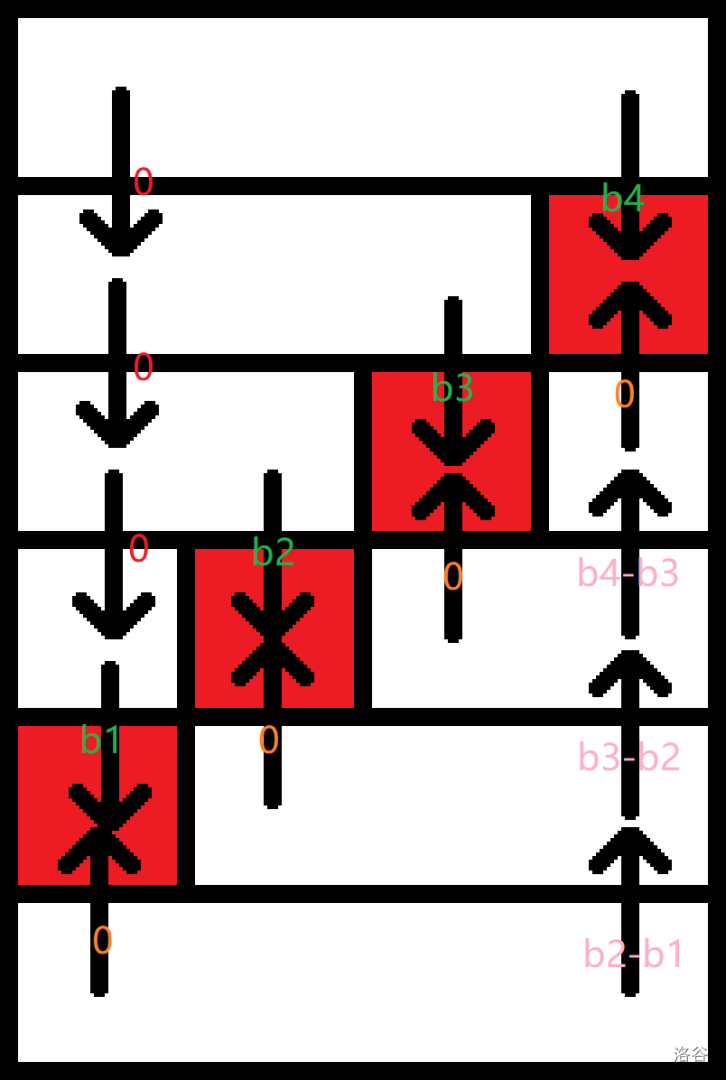
这个东西的优点在于分治的一半区间是定的,只需要知道一个点对另一半区间的贡献就可以简单递推,假设当前要求 \(i\) 对右边区间的贡献:
\(L_i-Ki\) 和 \(R_j-Kj\) 是关于 \(K\) 的一次函数,求出这俩玩意的和 \(\ge 0\) 的最小 \(K\) 实际上要求对于所有 \(j\),\(-L_i+Ki\) 和 \(R_j-Kj\) 的交点横坐标最小值,预处理出所有 \(R_j-Kj\) 的下凸壳后直接二分即可,复杂度降为 \(\log^2\) 可以轻松通过,效率是 std 的 \(\dfrac{1}{2}\) 左右