题解：P9245 [蓝桥杯 2023 省 B] 景区导游

题意：

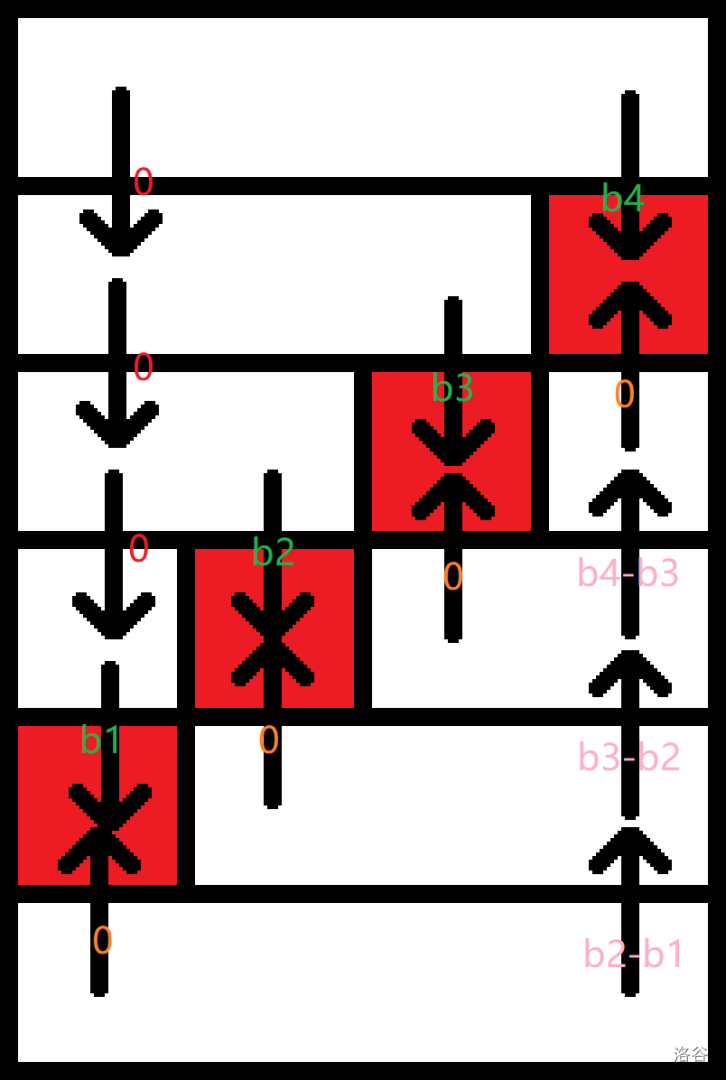
给出一个 \(n\) 节点的带权树和一个长度为 \(k\) 的原始路径 \(route\)，要求对于路径中每个点 \(i\)，求移去该点时所需的总代价。

思路：

注意到数据规模为 \(10^5\)，因此当算法时间复杂度为 \(O(n\log n)\) 时可以解决问题。对于一个含 \(k\) 个路径点的路径，对每个路径点 \(i\)，只需考虑两项：

● 相邻的 \(route[i-1]\) 到 \(route[i]\) 的距离 \(cost[i]\)；

● 跳过中间点（即 \(route[i-2]\) 到 \(route[i]\)）的距离 \(jump[i]\)。

遍历每个路径点 \(route[i]\) 时，分三种情况计算总代价：

\[ans(i)=\begin{cases}\sum_{j=3}^{k} cost[j], &i=1,\\\sum_{j=2}^{k-1} cost[j], &i=k,\\\sum_{j=2}^{i-1} cost[j]+jump[i+1]+\sum_{j=i+2}^{k} cost[j], &2\le i\le k-1.\end{cases} \]

为了高效计算区间内 \(cost\) 的累加和，可构造前缀和数组 \(pre\)。由此查询区间和的时间复杂度为 \(O(1)\)，而查询两点间距离的复杂度为 \(O(\log n)\)，总体这部分的时间复杂度为 \(O(k\log n)\)。

使用倍增求解公共祖先和距离，两点到公共祖先的距离和即为两点距离。可以选取任意节点作为根节点，这里我选取的是节点 \(1\)。通过 DFS 得到每个节点到根节点的距离，记：

\[dis[i]=\text{从节点 1 到节点 } i \text{ 的总距离} \]

同时构造倍增数组，其转移方程为:

\[fa[cur][i]=fa[fa[cur][i-1]][i-1] \]

对于任意两点 \(u\) 与 \(v\)，它们之间的距离为

\[dis[u]+dis[v]-2\cdot dis[LCA(u,v)] \]

其中 \(LCA(u,v)\) 为 \(u\) 与 \(v\) 的最近公共祖先。构造倍增数组的时间复杂度为 \(O(n\log n)\)，而利用 LCA 查询两点距离的时间为 \(O(\log n)\)。

因此，对于任意两点 \(x\) 与 \(y\)，可在 \(O(\log n)\) 内计算其距离，总体时间复杂度为 \(O((n+k)\log n)\)，即可满足题目要求。

#include <iostream>
#include <algorithm>
#include <vector>
#define int long longusing namespace std;vector<pair<int, int>> e[100005];
int n, m, k;
int fa[100005][25] = { 0 };
int dep[100005] = { 0 };int route[100005] = { 0 };
int dis[100005] = { 0 };
int jump[100005] = { 0 };
int pre[100005] = { 0 };void dfs(int cur, int from) {fa[cur][0] = from;dep[cur] = dep[from] + 1;for (int i = 1; i <= 24; i++) {fa[cur][i] = fa[fa[cur][i - 1]][i - 1];}for (auto [u, w] : e[cur]) {if (u == from) continue;dis[u] = dis[cur] + w;dfs(u, cur);}
}int lca(int x, int y) {if (dep[x] > dep[y]) swap(x, y);int dis = dep[y] - dep[x];for (int i = 0; dis; i++, dis >>= 1) {if (dis & 1) y = fa[y][i];}if (x == y) return y;for (int i = 24; i >= 0; i--) {if (fa[x][i] != fa[y][i]) {x = fa[x][i], y = fa[y][i];}}return fa[y][0];
}signed main()
{cin.tie(0)->sync_with_stdio(0);cin >> n >> k;for (int i = 1; i <= n - 1; i++) {int u, v, w;cin >> u >> v >> w;e[u].push_back({ v,w });e[v].push_back({ u,w });}for (int i = 1; i <= k; i++) cin >> route[i];dfs(1, 1);//pre[i]表示从route[1]依次到route[i]的总花费，jump[i]表示从route[i-2]跳到route[i]的花费。for (int i = 2; i <= k; i++) {int x = route[i - 1], y = route[i];int fa = lca(x, y);pre[i] = pre[i - 1] + dis[x] + dis[y] - 2 * dis[fa];if (i + 1 <= k) {int z = route[i + 1];fa = lca(x, z);jump[i + 1] = dis[x] + dis[z] - 2 * dis[fa];}}for (int i = 1; i <= k; i++) {int ans = 0;if (i == 1) ans = pre[k] - pre[2];else if (i == k) ans = pre[k - 1];else ans = pre[i - 1] + jump[i + 1] + pre[k] - pre[i + 1];cout << ans << " ";}return 0;
}

关于优化（主要集中在LCA）：

可以使用欧拉序列RMQ来 $ O(1) $ 查找父亲节点。因为本蒟蒻只会ST表RMQ，时间复杂度约为 $ O(n \log n + k) $；又因为该欧拉序列的大小是 $ 2n $，而 $ k\leq n $，因此反倒会因为常数较大比倍增慢。

欧拉序列+ST表RMQ：提交记录

朴素tarjan并查集能做到比倍增更优，但同欧拉序列一样，常数较大，不如重链剖分：提交记录

重链剖分可以把时间复杂度降到$ O(n + k\log n) $：提交记录

最后，不必构建前缀和数组。只需先求出完整走完的总花费，然后求移去某个节点后变化的花费即可。

以下是重链剖分且省去前缀和数组的AC代码，代码复杂度、时间复杂度和空间复杂度都较优：

#include <iostream>
#include <algorithm>
#include <vector>
#define int long longusing namespace std;vector<pair<int, int>> e[100005];
int n, m, k;
int dep[100005] = { 0 };
int fa[100005] = { 0 };
int siz[100005] = { 0 };
int son[100005] = { 0 };
int top[100005] = { 0 };int route[100005] = { 0 };
int dis[100005] = { 0 };
int jump[100005] = { 0 };
int to[100005] = { 0 };void dfs1(int cur) {siz[cur] = 1;for (auto [u, w] : e[cur]) {if (dep[u]) continue;dis[u] = dis[cur] + w;dep[u] = dep[cur] + 1;fa[u] = cur;dfs1(u);siz[cur] += siz[u];if (siz[u] > siz[son[cur]]) son[cur] = u;}
}void dfs2(int cur, int t) {top[cur] = t;if (!son[cur]) return;dfs2(son[cur], t);for (auto [u, w] : e[cur]) {if (u != son[cur] and u != fa[cur]) dfs2(u, u);}
}int lca(int x, int y) {while (top[x] != top[y]) {if (dep[top[x]] > dep[top[y]]) x = fa[top[x]];else y = fa[top[y]];}return dep[x] < dep[y] ? x : y;
}int getsum(int x, int y) {int fa = lca(x, y);return dis[x] + dis[y] - 2 * dis[fa];
}signed main()
{cin.tie(0)->sync_with_stdio(0);cin >> n >> k;for (int i = 1; i <= n - 1; i++) {int u, v, w;cin >> u >> v >> w;e[u].push_back({ v,w });e[v].push_back({ u,w });}for (int i = 1; i <= k; i++) cin >> route[i];dep[1] = 1;dfs1(1);dfs2(1, 1);int sum = 0;for (int i = 2; i <= k; i++) sum += to[i] = getsum(route[i - 1], route[i]);for (int i = 1; i <= k; i++) {int ans = 0;if (i == 1) ans = sum - to[i + 1];else if (i == k) ans = sum - to[i];else ans = sum - to[i] - to[i + 1] + getsum(route[i - 1], route[i + 1]);cout << ans << " ";}return 0;
}

最后，祝大家（还有我）蓝桥杯顺利......