题解写的非常简略,甚至一道题细节都没有清楚。
AGC067D
首先设排列为 \(1\sim n\) 是可行的。
第一感觉是相邻不可交换,即如果 \(l_i<i\),则 \(r_{i-1}=i-1\)。进一步地,\(r_{l_i\sim i}<i\),如果满足这个条件也易见其唯一性。
画在二维平面上,这等价于 \(y=x\) 每个点伸下去、伸到右边的线不相交(以下胡)。
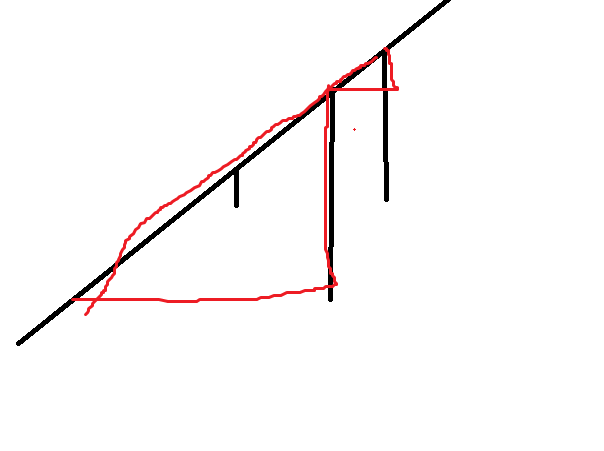
对红色的结构 dp,大概获得一维状态,,?
AGC067B
反转之后变成覆盖,大概可以写出类似于锤子 dp 的东西,但是问题是合并段的时候是无法去重,但是还真的没法去重。
但是结构比较简单,为了解决这个问题变成熔池计算,计算 \(f(l,r)\) 时直接容斥计算不可行方案即可,,,
AGC045D
策略就是从 1 开始不断点亮一个环。在所有灯点亮之前搞出 1~A 的自环或者 \(A+1\sim n\) 自立为环就寄了。用 GF 可以计算。
AGC062D
困难,,,
转切比雪夫,判定答案是否合法。首先设最大的是 \(D_M\),有解条件是 \(D_M\le 2\sum D_i\)。答案具有显然的界 \([D/2,D]\),然而这是很有好处的。
那么答案可以调整为这样的结构:走到正方形边界 \(X\) 上,徘徊一阵子,再走回来。这原因是任意点都可以在边境上徘徊。走到边界上可以的充要条件是:使用了若干 \(<X\) 的且和 \(\ge X\);使用了若干 \(<X\) 和恰好一个 \(\ge X\),满足小的加起来加上 \(X\) 大于等于大的那个。
枚举答案,由于徘徊可以任意,需要尽量构造去的和回来的;可以背包简易判断。
AGC036E
比较优秀的。相同的缩成一个,假设 \(cnt(A)\le cnt(B)=cnt(C)\),那么可以不断减除 BC 串,最终达到答案的上界 \(3cnt(A)\)。如果 \(C\) 还要更多,我就要尽量减除 C,使受影响的 A 最少。因此先删除 C 再删除 AC 即可。
AGC039F
搞一下相当于求两个矩阵 \(A,B\) 使得 \(B\) 的每个位置 \(B(x,y)\) 比 \(A\) 的 \(x\) 行 \(y\) 列的所有元素都要大。考虑结构没有办法,但是扫描值域,记录 \(A\) 插入完成了多少行列,交点处就是 B 可以插入的;新插入的贡献系数可以如如计算,总之这样得到了 poly 的复杂度。
AGC008F
钦定不可为全树,那么考察 \(N(x,d_1)=N(y,d_2)\) 相等的条件:存在路径中唯一结点使得其子树只覆盖了上面几层,别的子树覆完。这样如果 \(d_1<d_2\) 那么 \(y\) 可以向 \(x\) 移动易见仍合法,而如果 \(d_1=d_2\) 则两边都可以走一步。因此从这个过程得到这样的结论:
如果在最小的 \(d\) 上统计每个集合,这样的 \(d\) 唯一,且一个 \((x,d)\) 被统计的充要条件是 \(\not\exist y\in N(x),N(y,d-1)=N(x,d)\),这样解决了全是喜欢点的问题。
对于非喜欢点 \(N(x,a+b)\) 考察其可能和喜欢点 \(N(y,c+b)\) 相等的情况:此时设那个中间点是 \(z\),伸下去的距离是 \(b\),那么除非 \(x=z\) 那么 \(N(x,a+b)=N(z,b)\) 非最小,因此一个 \(N(x,d)\) 合法当全覆了一个包含喜欢点的子树。可以统计。
P10042 略
ARC122F
不少区间问题具有简单的贪心方法,然而转化为图论问题方便维护变化,之前的例子是选少点使得所有区间包含有点然而变成 LCT,这里又有例子。
显然红点是有序阶梯状物,然后做法是设某个蓝点 \(x\) 最终覆盖 \([l,r]\),就让 \(l\to x\to r+1\),同时任意 \(i\to i-1\),形成 \(k\) 个路径即合法。然而 \(l\to x,x\to r+1\) 是独立的,事实上可以连出权值为移动大小的边,这个连边可以前后缀优化建图,于是 \(k=1\) 是最短路问题,\(k\) 更大是费用流问题。
AGC043F TBC