二叉树相关题

1.二叉树最大深度

思路：

如果节点为空 (root === null)，表示这一部分的深度是 0。

如果节点不为空，递归地计算左子树和右子树的深度，然后返回左右子树深度的最大值加上 1（表示当前节点的深度）

代码实现：

function maxDepth(root) {// 基本情况：如果节点为空，深度为 0if (root === null) return 0;// 递归计算左子树和右子树的深度let leftDepth = maxDepth(root.left);let rightDepth = maxDepth(root.right);// 返回左右子树深度的最大值 + 1（当前节点的深度）return Math.max(leftDepth, rightDepth) + 1;
}

2.判断是否是对称二叉树

对称二叉树 是一种二叉树，其左右子树是镜像对称的。也就是说，树的左子树和右子树是完全相同的，只是左右节点的排列顺序是对称的。

判断二叉树是否对称

判断二叉树是否对称，通常可以通过递归的方法来实现。我们需要判断：

1. 根节点的左子树和右子树是否对称。

2. 如果左子树和右子树的左右孩子也是对称的，那么整个树就是对称的。

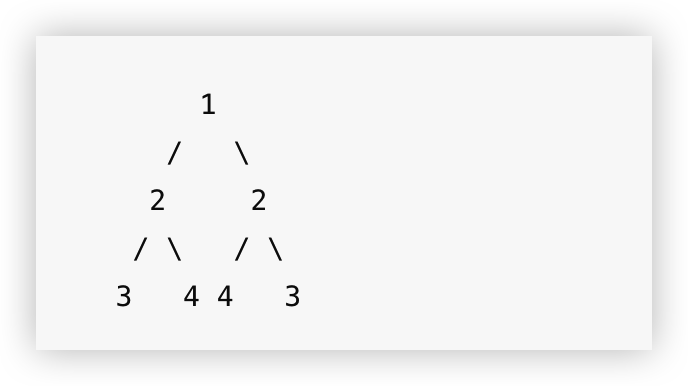
对称的二叉树

 

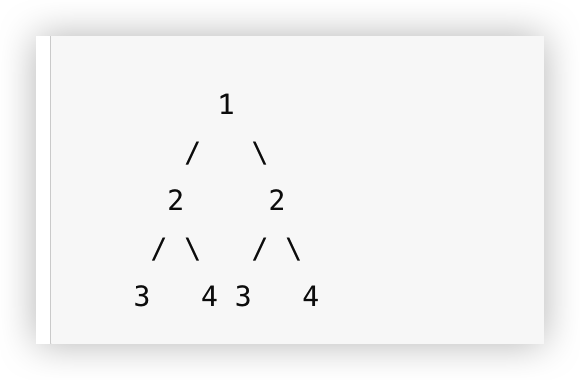
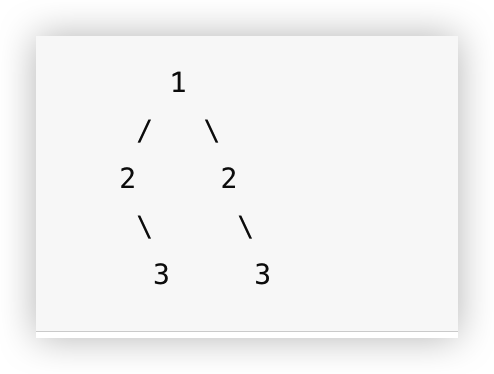
非对称的

 

function isSymmetric(root) {// 如果根节点为空，直接返回 trueif (root === null) return true;// 定义递归函数判断两个树是否是镜像对称function isMirror(t1, t2) {// 如果两个节点都为空，返回 trueif (t1 === null && t2 === null) return true;// 如果一个节点为空，另一个不为空，返回 falseif (t1 === null || t2 === null) return false;// 判断当前节点值是否相等，并递归判断左子树和右子树的对称性return (t1.val === t2.val) &&isMirror(t1.left, t2.right) &&isMirror(t1.right, t2.left);}// 判断根节点的左右子树是否是镜像对称的return isMirror(root.left, root.right);
}