【USparkle专栏】如果你深怀绝技,爱“搞点研究”,乐于分享也博采众长,我们期待你的加入,让智慧的火花碰撞交织,让知识的传递生生不息!
一、原理
参考这个论文:《Real-time Simulation of Large Bodies of Water with Small Scale Details》
核心是这两个公式:
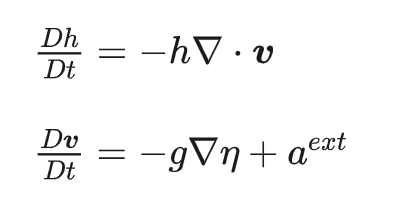
我在这篇《波动方程与浅水方程》中作了说明,转贴如下:
浅水方程:
(1)动量方程
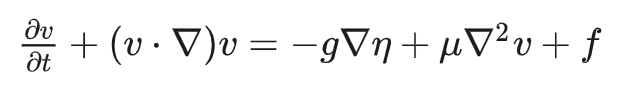
(2)质量守恒
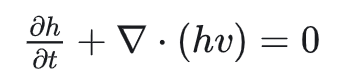
其实浅水方程的动量方程,就是在NS方程的动量方程

中令p=ρgη(η为海拔)得来,物理含义是表面隆起(或凹陷)产生压强(或负压强)。注意η和h的区别,h是水深,η是海拔,如果设河床高度为H,则有η=H+h。H是x,y的函数,h是x,y,t的函数。
对于普通水可以忽略粘性,进一步简化为:
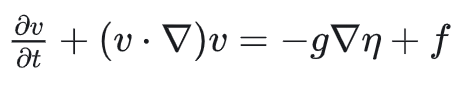
论文中所用公式为:
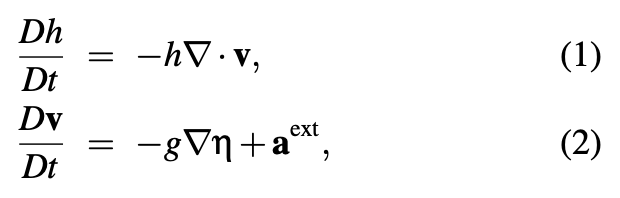
这其实就是浅水方程。说明如下:
D为物质导数,定义为
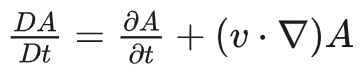
将(2)式中物质导数展开得
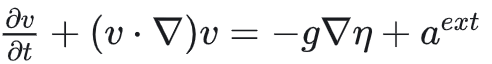
可见就是浅水方程的动量方程忽略掉粘性项。再看(1)式,将其中物质导数展开得
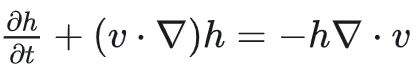
又因为h是标量v是向量且均为空间的函数,根据散度的运算性质,有
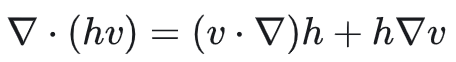
代入得
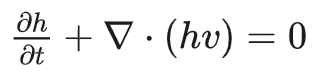
可见就是浅水方程的质量守恒方程。
注:
- 浅水方程的动量方程(2)用的是海拔η,质量守恒方程(1)用的是水深h,这正是它可以适用于凹凸不平地形,模拟洪泛的原因。假如我们强行让两方程都用h,那就相当于是假定海拔等于水深,即水底是平面,则不再具备模拟洪泛的能力,但仍可模拟水波。
质量守恒方程:
求解,对应论文中:

动量方程:
求解,其中求解对流项:
对应论文中:

由于没给公式,我暂时忽略了这项。
求解压力和外力项:
对应论文中:

二、MAC网格
论文中的离散化形式,含有:
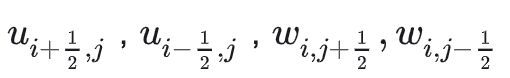
这种一半的项,是因为引入了称作MAC网格的技巧,即将流入/流出速度看作是在cell的边上,在处理散度相关问题时,经常用到。
下图很直观:
Eulerian Fluid Simulation Notes [Part 1]
Bridson's notes:nov17-cs533d-slides.ppt
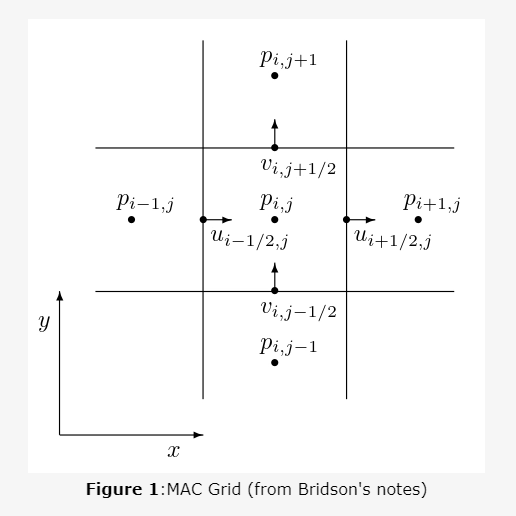
三、实现
最终是要用Shader实现,但初期验证算法出于Debug方便考虑,还是先用Houdini实现。
当然,我们可以真的在Houdini里建一个非常“具象的”MAC网格,就是每个格子表示一个cell,cell的边界上可以附加速度向量。
但为了将来转Shader更直接,我用的更接近二维数组的结构,我用一个二维点阵代表Grid,每个Point代表一个cell,Point有如下属性:
f@h=0;f@u_r=0;//即u[i+1/2,j] f@w_d=0;//即w[i,j+1/2] f@h_r=0;//即h[i+1/2,j] f@h_d=0;//即h[i,j+1/2]
至于为啥没有u_l(u[i-1/2,j]),w_u(w[i,j-1/2]),h_l(h[i-1/2,j]),h_u(h[i,j-1/2]),是因为当前Point的u_l其实就是左边格子的u_r,即它已经在左边格子中存过的,就没有必要在此格中再存一遍了。如果我们想获得u_l,只需如下:
int ID=@ptnum;int i=floor(ID/N);int j=ID%N;int ID_L=j*N+i-1;float u_l=point(0,"u_r",ID_L)
w_u,h_l,h_u同理。
这也正是论文中这段:
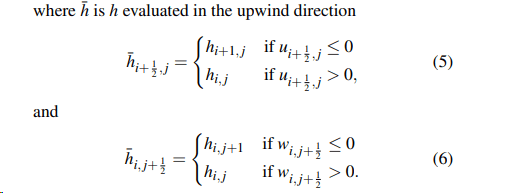
只给出
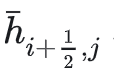
和
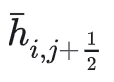
表达式,而没有写
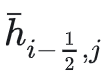
和
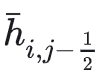
表达式的原因。因为当前cell的
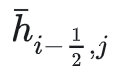
和
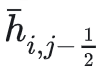
正是左边cell和上边cell(假设我的Grid是y轴向下)的

和
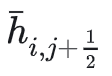
只要左边cell和上边cell已经计算过,就可以直接访问而无需在本cell中再重新计算一次。
同理,下面这段只给
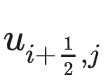
和
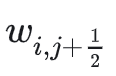
也是同样原因:

然后,就只是抄公式了。
四、稳定性
由于是离散模拟,而且用的是最简单的显式积分,所以会有数值稳定性问题,论文中列了几个措施可以提高稳定性:
Overshooting Reduction:
在论文的2.2节,提到有水与没水交界处,h的振幅会因数值问题而被放大,导致边缘出现尖刺甚至撕裂,用如下方法缓解:
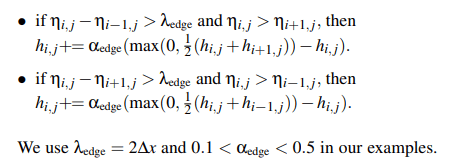
Stability Enhancements:
在论文的2.1.5节,提到如下约束可提高稳定性:

五、参数对效果的影响
g,α,Δx,Δt对效果均有影响。
例如,不同α值对比:
α=0.5
α=0.6
可见,α=0.5和α=0.6相比,由于速度限制更狠,显得更粘稠。
以上我们实现了凹凸不平地形上的浅水方程模拟,但忽略了对流项。
以下作了些改进,主要添加了对流项、涡度约束和边界条件。
效果
六、添加对流项
对流项:
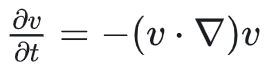
有两种实现方式:一种是Gather方法,一种是直接离散化方法。
(一)Gather方法
实际上在Gather方法之前,还有一个Scatter方法,这两种方法都是抛开对流的数学公式,而直接从公式背后的物理含义出发的模拟方法。Scatter方法就是把当前cell的属性传输出去,Gather方法就是把上游点的属性传输给当前cell。在《NS方程与2d流体模拟》中说过,Gather方法由于对GPU友好,更常用。
对流的Gather方法实现,可以参考《游戏中的流体模拟(Fluid Simulation),技术美术教程 》。
由于我要在之前的基础上加对流,而那个模拟过程中只使用到边速度,但上面教程中的实现用的是cell速度,所以需要在边速度和cell速度之间互转。
过程如下:
Pass1:由边速度计算cell速度。
Pass2:计算对流Advect。
1.用9个格加权平均估算当前cell平滑速度。
2.将当前cell平滑速度乘以dt再反向,以此作为偏移量去采样上游目标点的速度(用双线性插值)。
3.用采到的速度替换当前cell的速度。
Pass3:由cell速度计算边速度。
其中需要注意的点有:
1.边速度与cell速度之间的互转。
我问的ChatGPT:

由于两个问题我是连续问的,所以它给出的公式也恰好是互逆的。我验证了一下,如果把Pass2屏蔽,只剩Pass1和Pass3,结果确实不受影响。
2.无水处的速度
用9个cell的速度加权平均计算当前cell平滑速度时,不用管各cell是否有水,照加不误。采样上游点速度覆盖当前cell速度时,也不用管上游点处是否有水,照覆盖不误。原因是,只要能保证无水处速度是0,上面的计算就都是合理的。至于如何保证无水处速度为0,见后面"边界条件"一节。
3.数值稳定性及对流快慢和强度控制
以下两项措施可以提高对流的数值稳定性:
(1)缩短步长:将偏移-V*dt采样改为偏移-V*dt*0.5采样,这样虽然会导致对流变慢(如果滴入墨水的话,体现为墨水扩散变慢),但有助于数值稳定性。如果将步长减半的同时又不想对流变慢,可以在一帧内将对流迭代两次。
(2)减弱影响:将“用目标点速度覆盖当前点速度”这一步,改为不完全覆盖,而是按一定比例(如0.5)进行混合。这样虽然会使对流效果减弱,但也有助于数值稳定性。
是否缩短步长和减弱影响,也未必总是出于数值稳定性考虑,有时候为了效果,也需要对对流的快速和强度进行控制。
4.边框处理
计算当前cell平滑速度时,9个cell中超出边框者要去掉。采样上游点时,如果上游点超出边框,则放弃当前cell的对流计算。
(二)直接离散化方法
就是将
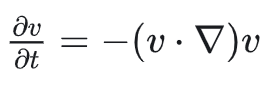
展开为(设v=(u,w)):

其中右边各项离散化如下:
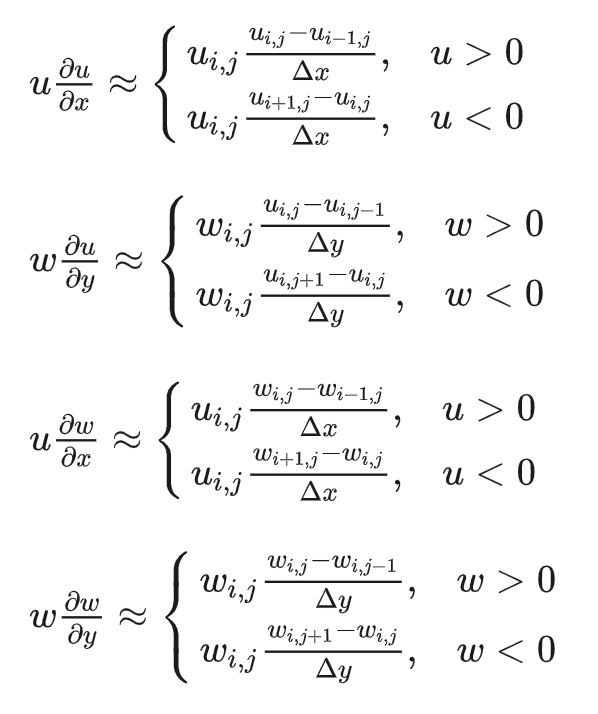
这里用的是迎风格式,参考ChatGPT:

同样可以用缩短步长和减弱影响对对流快慢和强度进行控制,以及提高数值稳定性。
七、添加墨水
要想让对流效果明显地显示出来,需要添加墨水。
方法如下:
1.标记一些cell为inkSource。
2.每帧对标为inkSource的cell追加ink值:ink+=inkAmount*dt
3.在解算对流时:
如果用的是Gather方法,则除了用上游点的速度覆盖当前点速度外,还要用上游点ink覆盖当前点ink。如果用的是直接离散化方法,则除了计算du、dw,(u,w)+=(du,dw),还要计算dink,ink+=dink。
4.最后将ink可视化。
八、两种对流方法效果对比
左边为Gather,右边为直接离散化
可见,大致效果接近,由于两种方法很不同,所以基本可佐证实现是正确的。
九、添加涡度约束
方法在《NS方程与2d流体模拟》中已经写过。
需要注意的一点是,如果GetCurl函数中没有除以Δx,则要在外面补上。另外为了让效果与时间解耦,最终速度调整量还应乘以Δt。
有无涡度约束对比:

左:无涡度约束,右:有涡度约束
可见,区别还是很明显的。
十、添加边界条件
1.边框处理
在之前的文章中,我没有限制水不能流出边框,所以水一直沿着河道流,永远不会漫上来。
这次,我加了水不能流出边框的限制,只需将边框视作障碍物,每帧末尾将边框cell的边速度和cell速度均标为0即可。这在论文《hfFluid.pdf》中有写:

2.使无水处速度为0
浅水方程本身是无法保证无水处速度为0的,因为从
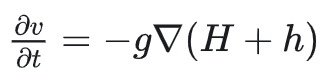
来看,当无水,即h=0时,变为
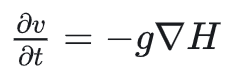
即仍会由于地形本身有梯度而产生速度。所以,要想让无水处速度为0,只能通过人为添加约束实现。
其实,上面Boundary Conditions这段已经给出了方法,就是通过
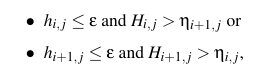
判断右侧边(i+1/2,j)是否为“岸”。类似方法也可以判断出左、上、下各边是否为岸。
而且分析一下会发现,这种判断方法下,不仅岸与非岸的交界边会被判为岸,岸上的边也都会被判为岸,这正是我们想要的。于是对于判断为岸的边,我们在每帧末尾将其边速度强制设为0,则可实现无水处速度为0的目标。至于cell速度,由于它是由边速度算出的,所以只要边速度标对了,cell速度自然也就对了。
另外,由于我们是在每帧末尾将无水处速度标为0的,所以我将对流的计算放在最前面,以保证对流计算是在无水cell速度为0的情况下进行的。
下图是不加岸边速度置0(左)与加岸边速度置0(右),速度场及最终效果对比:
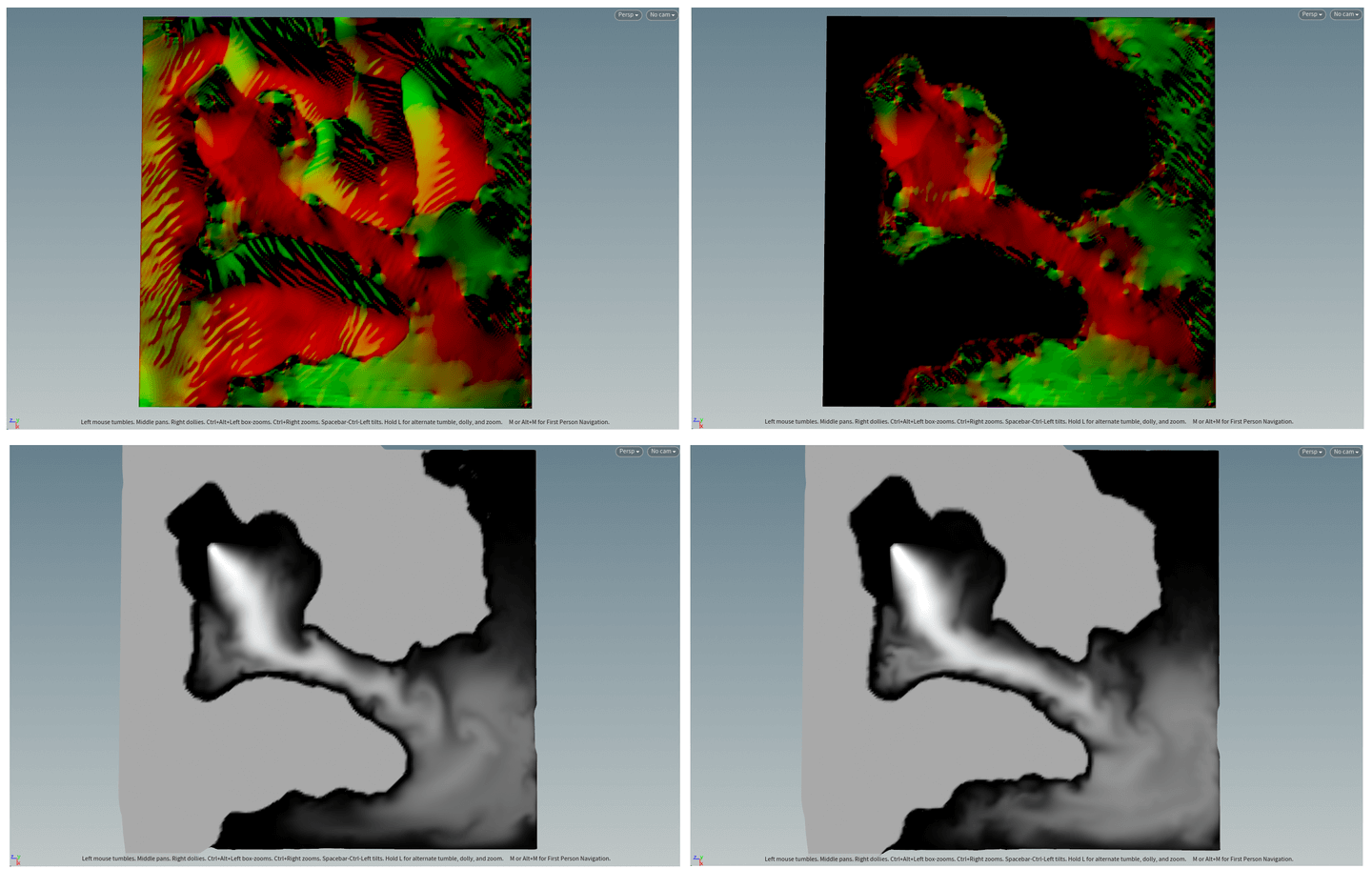
左:不加岸边速度置0,右:加岸边速度置0
看起来似乎差别不大,但有一点,如果近看的话,会发现岸边速度不置0的模拟结果,水会在岸边隆起,不太合理,而加了岸边速度置0的模拟结果,水与岸边则是比较平滑的过度,如图所示:

左:不加岸边速度置0,右:加岸边速度置0
这是侑虎科技第1787篇文章,感谢作者杨超wantnon供稿。欢迎转发分享,未经作者授权请勿转载。如果您有任何独到的见解或者发现也欢迎联系我们,一起探讨。(QQ群:793972859)
作者主页:https://www.zhihu.com/people/wantnon
再次感谢杨超wantnon的分享,如果您有任何独到的见解或者发现也欢迎联系我们,一起探讨。(QQ群:793972859)