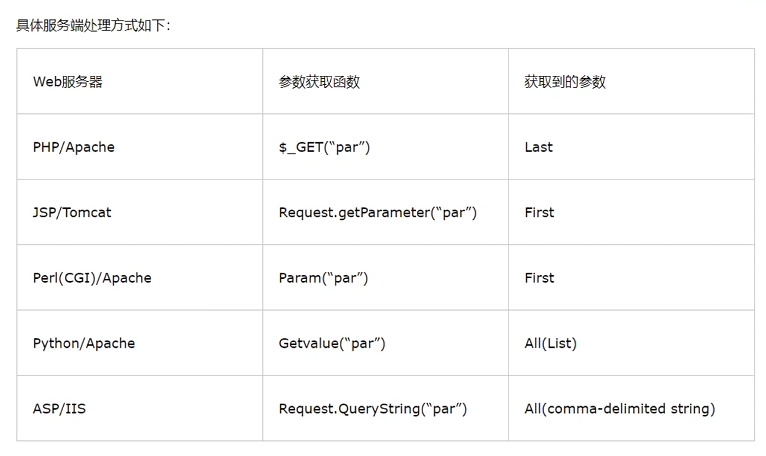
https://codeforces.com/contest/2091/problem/F


这题主题思路就是递推,从下往上递推,然后用差分和前缀合得到下一行可能性,详细看代码注释
点击查看代码
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
const int MOD = 998244353;//模数
const int N = 2222;//图的最大范围
int dp[N][N][2];//dp每个点有两种状态
string str[N];void solve(){int n,m,d;cin>>n>>m>>d;//获取范围和最大距离for(int i = 1;i<=n;++i){for(int j = 1;j<=m;++j){dp[i][j][0] = dp[i][j][1] = 0;//初始化dp}}for(int i = n;i>=1;--i){string s;cin>>s;str[i] = "0"+s;//存储从下到上的点,然后位置从1开始}for(int j = 1;j <= m;++j){//遍历最下面的一行,找到可攀岩点记录为1if(str[1][j]=='X')dp[1][j][0]=1;//第一层每个点有攀岩的地方初始为一}for(int i = 1;i<=n;++i){ //从上到下开始每行遍历for(int j = 1;j<=m;++j){if(str[i][j]=='#')continue;//如果是不可攀岩点就跳过int l = max(1,j-d),r = min(m,j+d);//l找欧拉距离内最左边的点,r同理找最右点,为当前点最左和最右dp[i][l][1] = (dp[i][l][1] + dp[i][j][0])%MOD;//该点最左边出点为该入点的可能性和(这里用差分)dp[i][r+1][1] = (dp[i][r+1][1] - dp[i][j][0] + MOD)%MOD;//该点最右边出点为该入点的可能性和}for(int j = 1;j <= m;++j)dp[i][j][1] = (dp[i][j][1] + dp[i][j-1][1])%MOD;//前缀和if(i==n)continue;//如果到最后一行就跳过for(int j = 1;j <= m;++j){//再遍历当前行的每个点int len = d*d-1;//欧拉距离*欧拉距离-1len = sqrt(len);//长度的平方。(这里是勾股定理,d是斜边)int l = max(1,j-len),r = min(m,j+len);//获取该点最左边和最右边if(str[i][j]=='#')continue;//如果没攀点就跳过可能性的合并dp[i+1][l][0] = (dp[i+1][l][0] + dp[i][j][1])%MOD;//该点最左边的距离的下一层加上这个点的可能性(差分)dp[i+1][r+1][0] = (dp[i+1][r+1][0] - dp[i][j][1] + MOD)%MOD;//最右边的点减去这个点的可能性(差分)}for(int j = 1;j<=m;++j)dp[i+1][j][0] = (dp[i+1][j][0] + dp[i+1][j-1][0])%MOD;//前缀和合并下一层可能性}ll ans = 0;for(int j = 1;j<=m;++j){if(str[n][j] == 'X')ans = (ans + dp[n][j][1])%MOD;//有最后一层有盘点的加入可能性里面}cout<<ans<<endl;//总结,主体思路用差分来更新欧拉距离最左和最右端,然后前缀和得到每层可能性(先不管他有没有攀点)最后再遍历最上面//判断没有攀点的就合并可能性
}
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);ll t=1;cin>>t;while(t--){solve();}return 0;
}