参考博客:
论文解读二代GCN《Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering》 - 别关注我了,私信我吧 - 博客园 (cnblogs.com)
摘要
为将CNN推广到高维图结构数据中,基于spectral graph theory(谱图理论),设计了一种通用的fast localized convolutional filters。优势有如下:具有和经典卷积神经网络相同的
- linear computational complexity
- constant learning complexity
Introduction
在图像、视频等领域,卷积神经网络借助于局部卷积滤波器或者内核识别来提取数据中的局部特征,并组合成多尺度层次模式。
而社交网络的用户数据、生物网络的基因数据等等位于非欧几里得域的数据,一般是通过图结构来进行描述,因其能够对于异质成对关系进行很好的表示。
因此,将卷积和池化操作推广到图结构是本文的目标,主要贡献有以下:
- Spectral formulation
- Strictly localized filters
- Low computational complexity
- Efficient pooling
- Experimental results
Proposed Technique
文中提出了三个步骤:
- 设计图上局部滤波器
- 图粗化
- 高效的图池化过程
局部滤波器
文中,作者提出了一种多项式参数化的滤波器,使得学习复杂度从非参数化滤波器的O(n),降低到了O(K),K是滤波器的支撑大小,因此,复杂度降低到了与经典卷积神经网络相同的复杂度。
图粗化
在这个过程中,作者使用Graclus算法对于相似结点进行相应的合并,进而每次减少约一半的结点。
但是,值得注意的是,每次图粗化后,图的拓扑结构会发生相应的变化,因此需要求相应的拉普拉斯矩阵。
图池化过程
从文中可知,首先使用 Graclus 算法对图进行粗化,在每一层粗化时,Graclus 的贪心规则是在每一个粗化层级选取未标记顶点并与邻居匹配,匹配完标记节点并设置粗化后的权重,重复操作直到所有节点被处理,得到不同层级的粗化图(如G1、G2等),此时顶点是无特定有意义排列的。
之后分两步进行处理,一是创建平衡二叉树,为使每个节点都有两个子节点,会添加虚拟节点(fake nodes)与单例节点配对;二是在最粗层级任意排序节点,然后将排序传播到最细层级,从而在最细层级得到规则的顶点排列。
这个时候,对于池化操作进行处理时,就会近似于一维池化操作,内存的访问是局部性的,利于GPU并行架构。
TIP:图粗化过程
graph coarsening procedure 即图粗化过程,是将卷积神经网络推广到图结构中的一个重要步骤,旨在为池化操作提供有意义的邻域,同时保留图的局部几何结构。
TIP:匹配局部领域的挑战
- 图结构的不规则行:图中节点的连接方式复杂多样,不像规则网格有固定的邻域模式。在规则网格上,如二维图像像素,邻域相对固定,卷积操作能以统一方式提取特征。但在图中,不同节点的邻居数量和连接关系差异大,难以用统一规则确定和处理局部邻域 。例如,社交网络中,某些节点可能有大量邻居,而有些节点邻居很少,这使得设计能适用于所有节点的局部卷积滤波器变得困难。
- 缺乏统一平移定义:在空间域中,图上没有像规则网格那样明确、唯一的平移概念。在图像等规则网格中,平移操作很明确,卷积核可按固定方向和步长滑动。但在图中,节点排列无规律,无法简单定义平移,这导致难以实现类似规则网格的卷积操作,影响滤波器在不同位置提取相似特征的能力,增加了匹配局部邻域的难度 。
TIP:池化后的反向传播
池化后改变了图的尺寸,是一个不可导的环节,因此,我们需要思考如何进行反向传播。

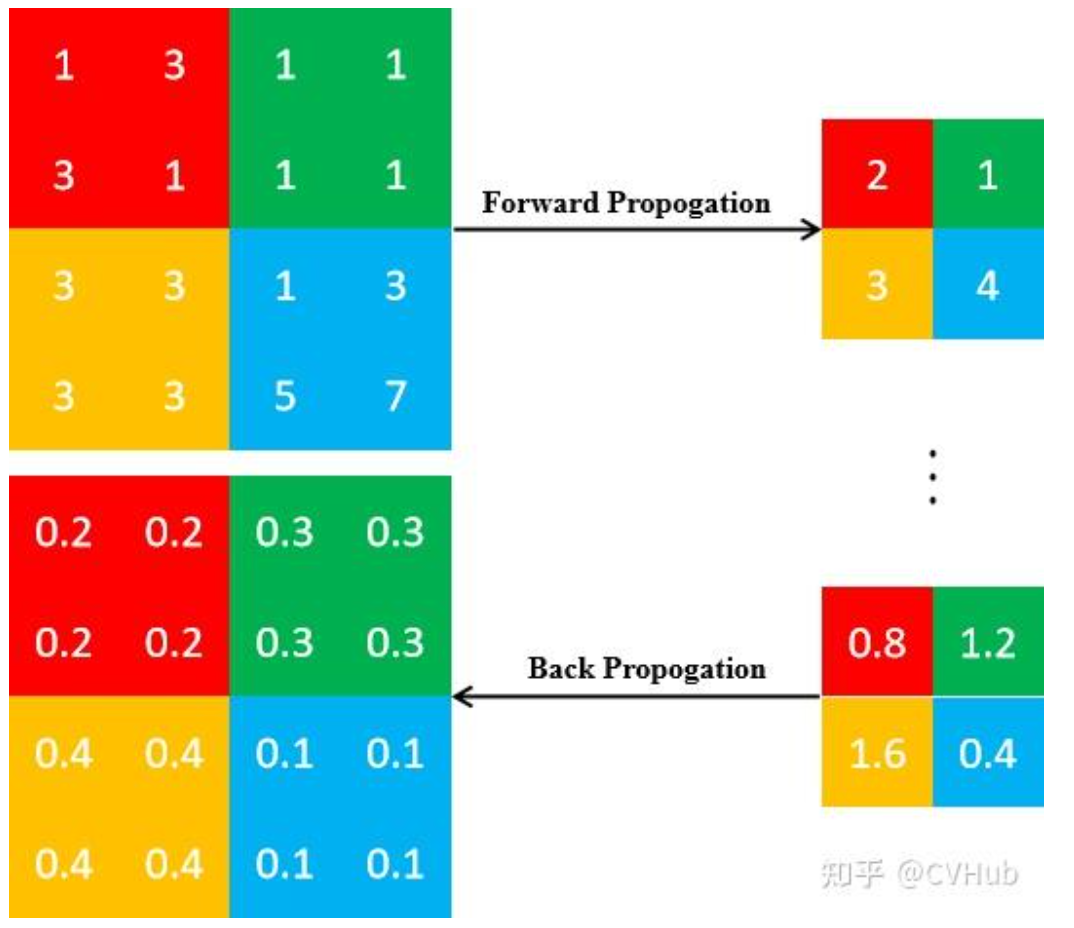
- 平均池化
对于平均池化来说,由于当前位的元素是由区域内所有元素取平均值所得,因此该梯度和为所有元素的梯度之和。因此,我们在反向传播的过程中只需将当前位的梯度值均分即可。
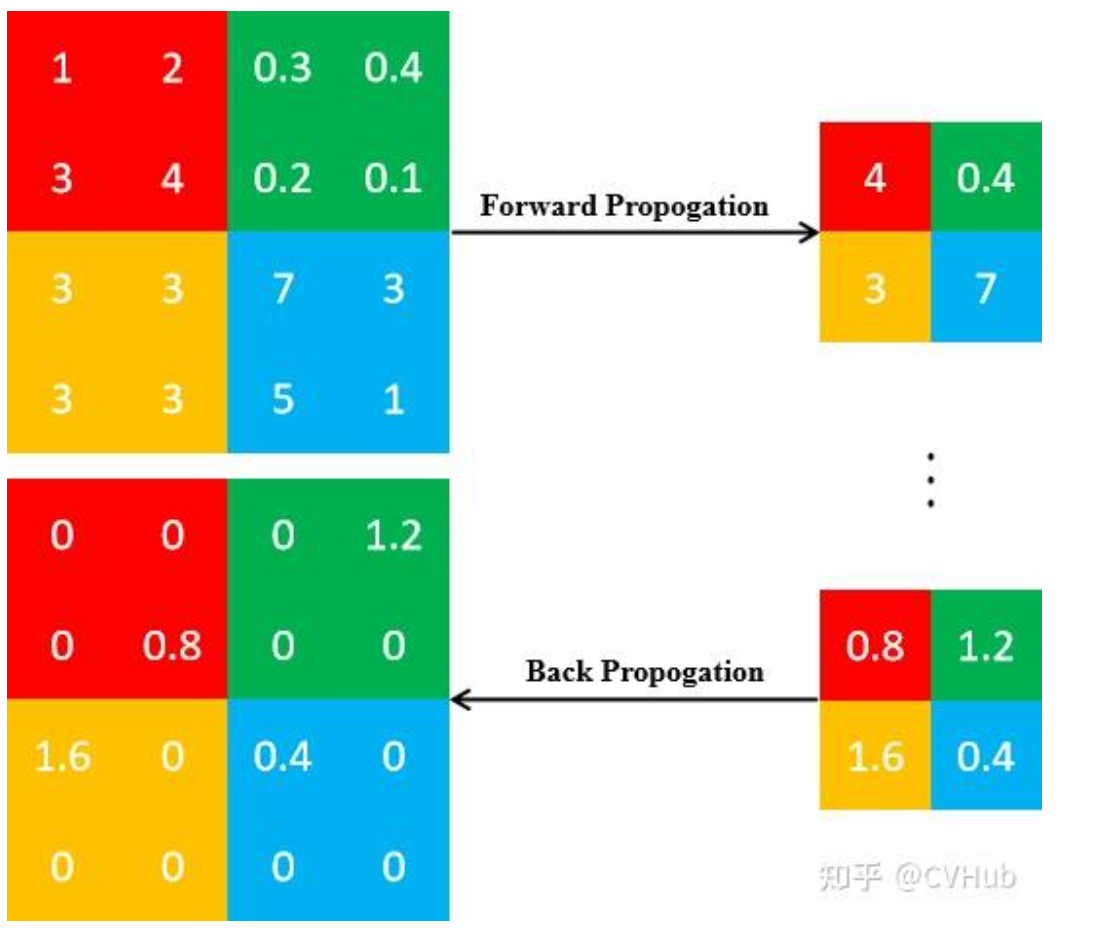
- 最大池化
对于最大池化而言,由于当前位的元素是由区域内所有元素取最大值所得,因此该梯度和仅取决于该位的元素,即其余元素的梯度应置为0。因此,我们在前向传播的过程中应该记录该最大值的位置索引。
Related Work
-
图信号处理
弥合信号处理与谱图理论之间的差距,将一系列卷积、平移等一系列操作在保留原有直观概念的同时,引入到图数据当中。 -
非欧领域的卷积神经网咯
主要提及了一些之前的工作
实验
数据集:
MNIST
20NEWS