稀疏矩阵向量乘法介绍

稀疏矩阵向量乘法介绍

稀疏矩阵向量乘法（SpMV）是每个隐式稀疏线性代数求解器。从简单的 Krylov 算法到 multigrid 的算法性能方法在很大程度上取决于 SpMV 实现的速度。因为 SpMV 具有非常低的算术强度，定义为浮点操作数，则实现速度受内存带宽。最大化内存带宽的实现将实现卓越的性能与简单方法相比。或者，利用稀疏矩阵中固有的任何结构，从而最大限度地减少内存数量所需的访问，也将实现卓越的性能。将开发广义 SpMV 操作

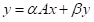
 的 HIP 实现y=αAx+βy的几个标准 SpMV 实现，包括：

1）标量压缩稀疏行 （CSR）

2）向量 CSR

3）ELLPACK格式

4）阻止 ELLPACK

许多常见的 SpMV API，例如 rocSparse、 使用此通用接口。希望在实现和 ROCm 中提供的实现。在 SpMV 公式中，

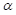
 和

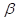
 是标量值，

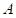
 是大小为

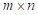
 的稀疏矩阵，

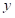
 是密集的向量的大小为

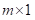
 ，并且

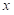
 是大小为

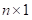
  的密集向量。一个 key 矩阵的统计数据，每行的非零数

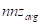
 。将工作分配给不同的 GPU 计算资源通常基于此度量。

首先，将回顾稀疏矩阵中广泛使用的 CSR 和 ELLPACK 格式。在描述完实现之后，将在 AMD MI250X 架构上比较相对性能，用于各种稀疏矩阵。转换算法从一种矩阵存储格式到另一种矩阵存储格式可能是一项昂贵的工作。代码示例将提供 CSR 和 ELLPACK。

1. 存储格式

对不同稀疏矩阵存储类型的回顾最好用一个简单的例子来说明。如图10-1所示，显示了一个有12个非零的5×5矩阵。这个稀疏矩阵的坐标（COO）格式由3个长度相同的数组组成，用于行、列和值。对行和列使用基于0的索引。数据按行主顺序排序，以便行0的所有数据都列在第一位。接下来是第1行、第2行…。

 

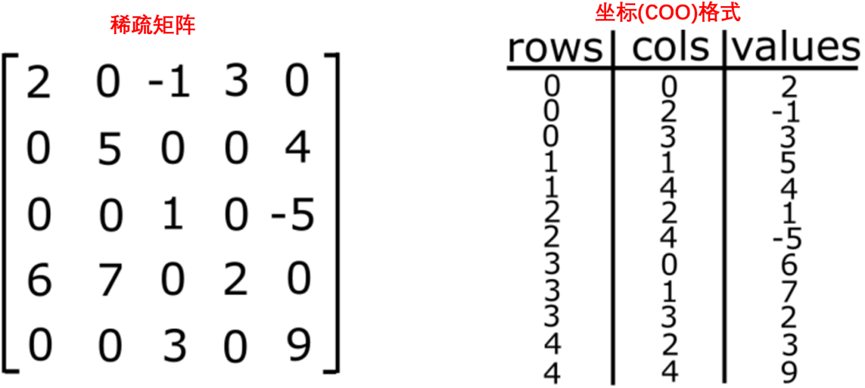
图10-1 稀疏矩阵存储格式

2. 压缩稀疏行（CSR）格式

用于存储稀疏矩阵的CSR格式，源于对上述行数据结构的简单压缩。只需计算每行中非零条目的数量。然后，行计数的累积和算法完成了计算。压缩的行数据结构（以下称为行偏移量）的大小为m+1。第一个值是0，其余值是累积和的结果。这种数据结构非常有用，因为通过相邻读取为每个稀疏矩阵行乘以密集向量（即稀疏点积）计算，提供了开始和结束索引。压缩稀疏行（CSR）格式，如图10-2所示。

 

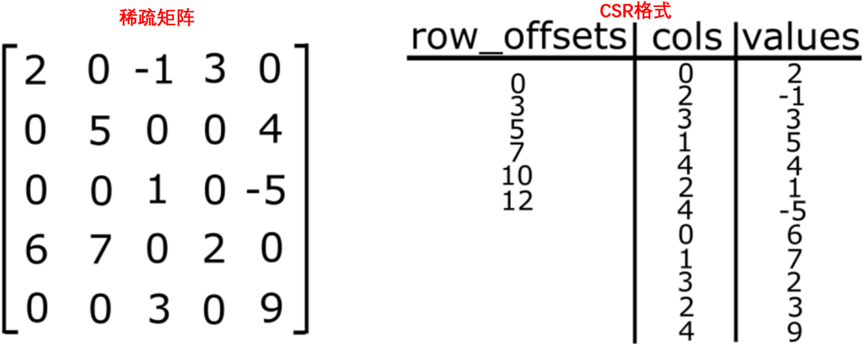
图10-2 压缩稀疏行（CSR）格式

3. ELLPACK 格式

当每行非零个数的变化很小时，ELLPACK格式是SpMV的有效数据结构。与CSR相比，该格式将存储的顺序颠倒为列主，并使用零填充来实现数据结构的一致性。每行的条目数由所有行的最大值决定。任何非零数少于最大值的行，都有0个填充值和列索引的合理值。例如，可以在行中填充最后一个有效的列索引，以确保重新读取之前加载的索引和值对。

可以将此数据结构可视化为将数组中的所有值（和列索引）向左移动。

    稀疏矩阵ELLPACK格式，如图10-3所示。

 

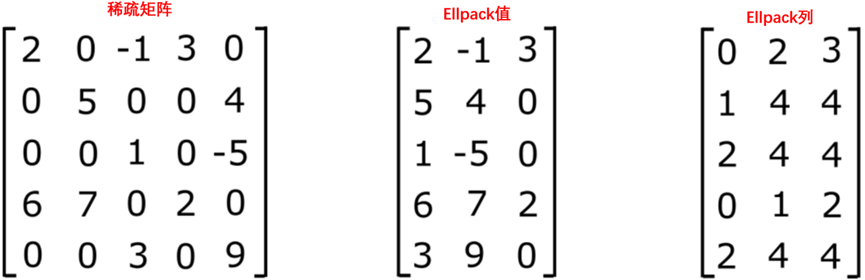
图10-3 稀疏矩阵ELLPACK格式

通过以行块的形式形成ELLPACK数据结构，可以进一步优化ELLPACK格式。这最大限度地减少了零填充量，同时实现了数据的一致性。将此称为封锁ELLPACK。