leetcode每日一题：图中的最长环

题目

2360. 图中的最长环

给你一个 n 个节点的 有向图 ，节点编号为 0 到 n - 1 ，其中每个节点 至多 有一条出边。

图用一个大小为 n 下标从 0 开始的数组 edges 表示，节点 i 到节点 edges[i] 之间有一条有向边。如果节点 i 没有出边，那么 edges[i] == -1 。

请你返回图中的 最长 环，如果没有任何环，请返回 -1 。

一个环指的是起点和终点是 同一个 节点的路径。

示例 1：

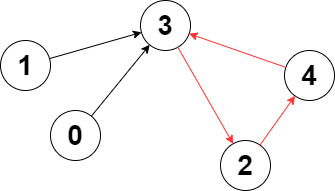
输入：edges = [3,3,4,2,3]
输出去：3
解释：图中的最长环是：2 -> 4 -> 3 -> 2 。
这个环的长度为 3 ，所以返回 3 。

示例 2：

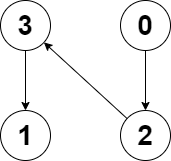
输入：edges = [2,-1,3,1]
输出：-1
解释：图中没有任何环。

提示：

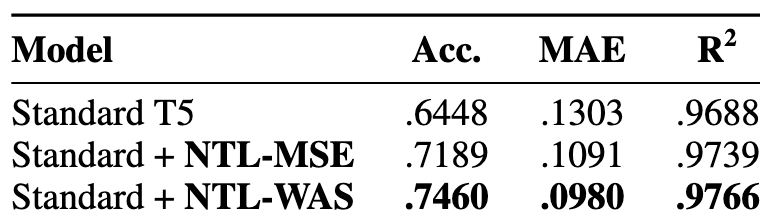
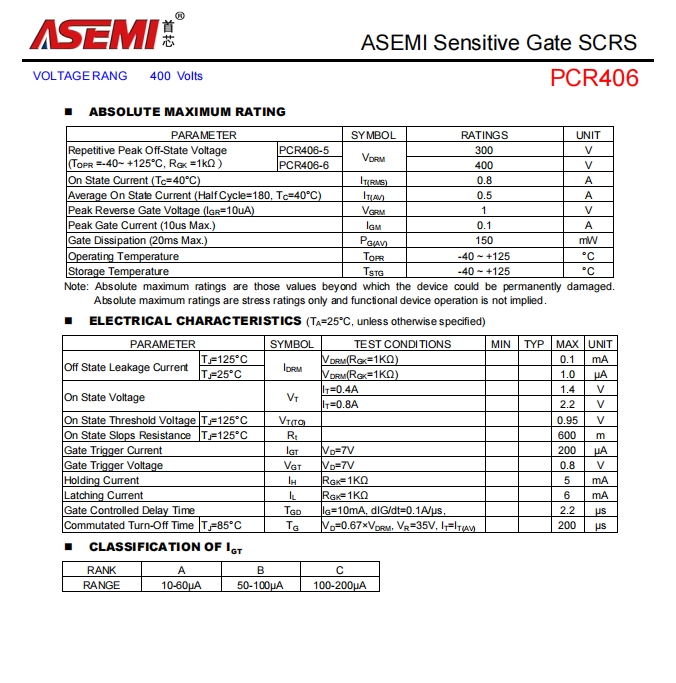
• n == edges.length
• 2 <= n <= 105
• -1 <= edges[i] < n
• edges[i] != i

思路

​ 不要被难度级别“困难”吓倒，其实读懂题目后，好像也没那么难。题意说人话就是，有向图中每个节点最多只有1条出边，求这个图中最大的环包含的节点数量，如果没有环，则返回-1。
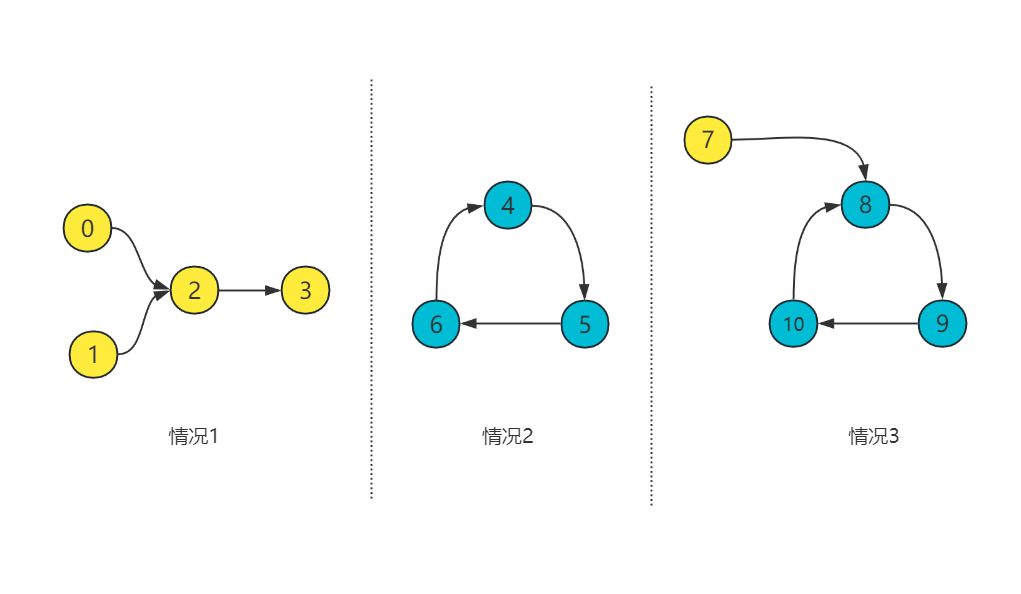
​ 题目并不保证整个图是全部连通的，所以，我们可以先把这个图分成若干个不连通的部分，在每个部分内部，是连通的。那每个部分有如下三种情况

• 无环，是若干个存在公共节点的链表
• 有环，而且所有节点都在环内
• 有环，部分节点在环内，部分节点在环外

​ 因为题目保证了每个节点最多只有1条出边，所以确定了起始点后，往后遍历的路径是唯一的。对于无环的情况，我们无论从哪个节点开始遍历，最后都不会成环；对于情况2和情况3有环的情况，无论我们从哪个节点开始遍历，最终一定可以遍历到环内的节点，且可以重复走到环内的每个节点。

​ 所以，我们可以采取这样的策略，每次遍历一个节点，全局时间time++：外层，从下标0到n-1作为每个连通部分的起点进行遍历，内层，通过firstVisitTime[]数组来记录这个节点第一次被遍历到的时间，如果时间是0，证明这个节点没有被遍历过。另外，我们还需要一个变量记录每个连通部分第一次被遍历到的时间partBegin，如果firstVisitTime[i] >= partBegin，证明确实是在这个连通部分遍历的，那么当前时间减去firstVisitTime[i] 就是这个环的大小了。

图解

代码

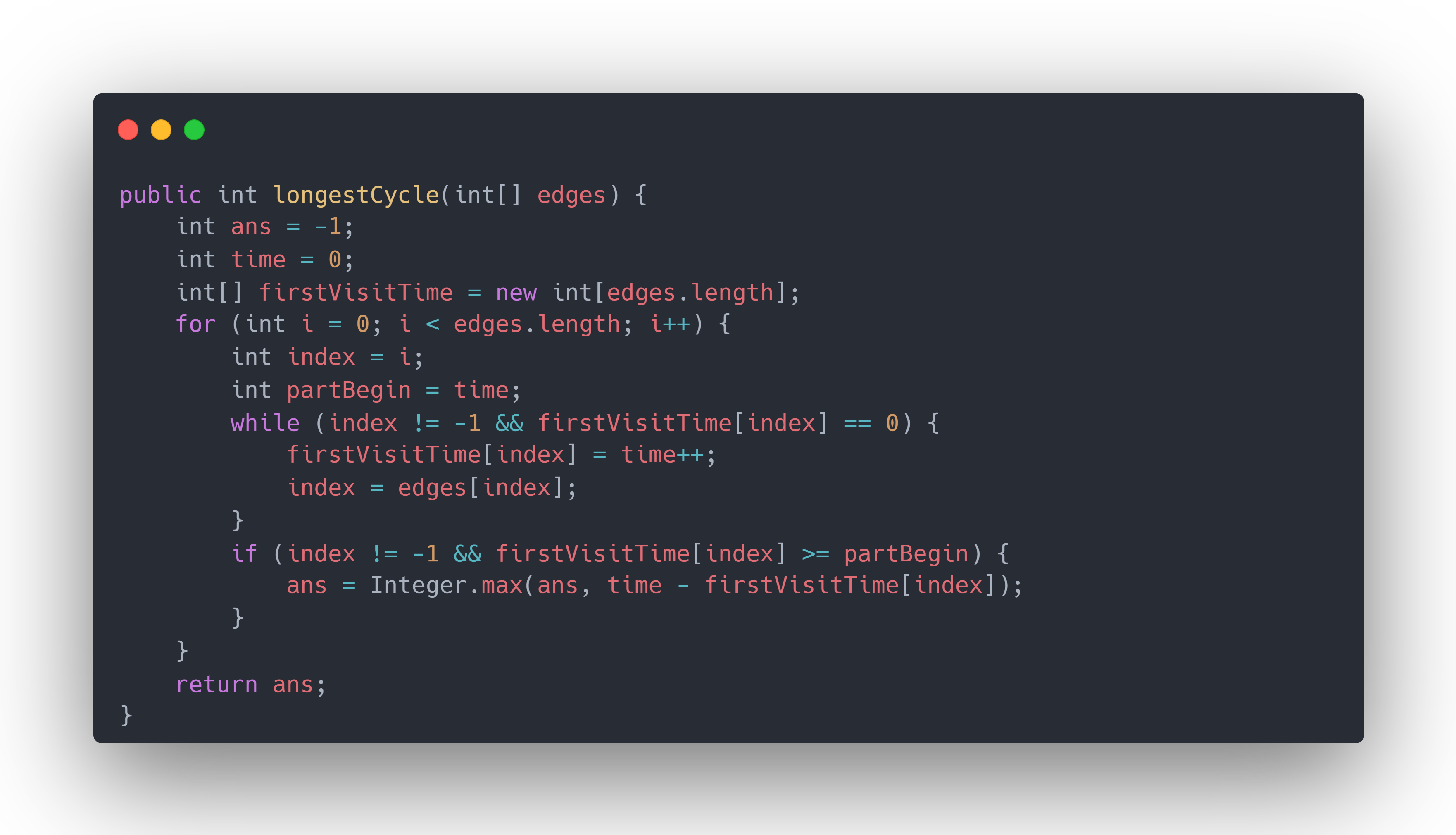
public int longestCycle(int[] edges) {int ans = -1;int time = 0;int[] firstVisitTime = new int[edges.length];for (int i = 0; i < edges.length; i++) {int index = i;int partBegin = time;while (index != -1 && firstVisitTime[index] == 0) {firstVisitTime[index] = time++;index = edges[index];}if (index != -1 && firstVisitTime[index] >= partBegin) {ans = Integer.max(ans, time - firstVisitTime[index]);}}return ans;
}

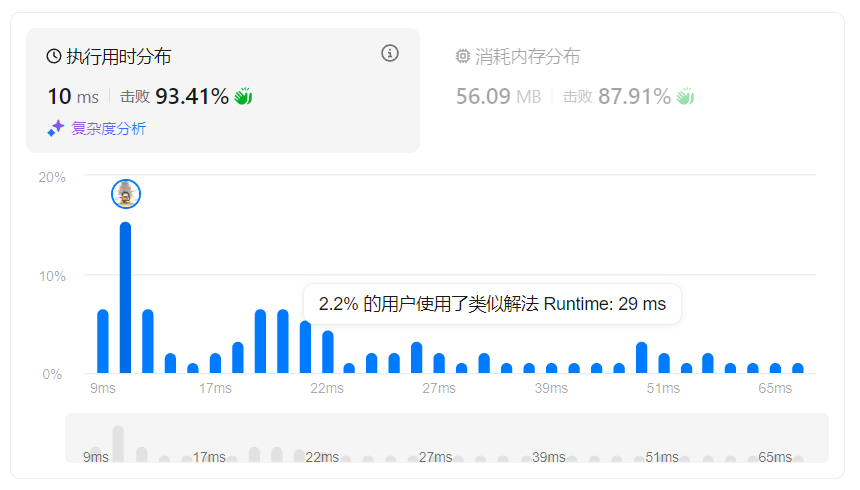
耗时