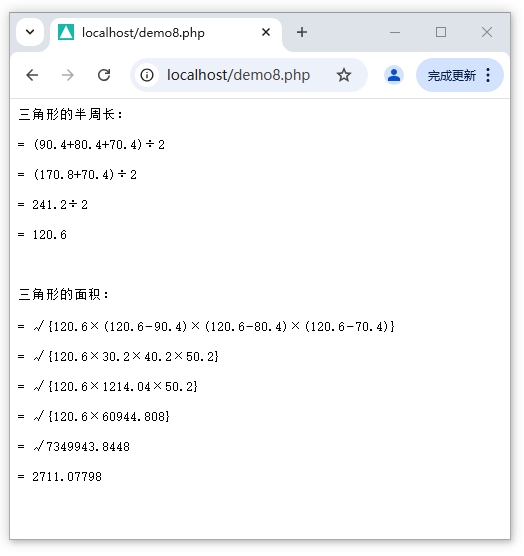
k 维 FWT。
考虑到 FWT 运算过程的实质:
\(FWT(A)[i]=\sum_{j}w(i,j)A_j\)
我们要求 \(FWT(A)[i]·FWT(B)[i]=FWT(C)[i]\),令系数相等,也就是要求
\(\sum_{j,k}w(i,j)w(i,k)A_jB_k=\sum_{t}w(i,t)C_t=\sum_{t}w(i,t)\sum_{j\oplus k=t}A_jB_k\)
也即是 \(w(i,j)w(i,k)=w(i,t),j\oplus k=t\)
由于 \(\oplus\) 是一个位运算,因此不妨考虑按位构造 \(w(i,j)=w(i_0,j_0)w(i_1,j_1)\dots w(i_n,j_n)\),其中每一位的 \(w\) 是独立的。
注意到我们需要 \(IFWT\),也即是 \(w\) 矩阵是一个可逆矩阵,也即是 \(w\) 矩阵满秩。
对于二维的情况,例如
-
\(w(i,j)w(i,k)=w(i,j\&k)\),可以写作 \(w(i,j)=[i\&j=j]\),将其拆为二进制的每一位,也即是 \(w(0,0)=w(1,0)=w(1,1)=1,w(0,1)=0\)
-
\(w(i,j)w(i,k)=w(i,j\oplus k)\),可以写作 \(w(i,j)=(-1)^{popcnt(i\& j)}\),这是因为 \(popcnt(i\&j)+popcnt(i\&k) \equiv popcnt(i\&(j\oplus k))\)
将其拆为二进制位,也即是 \(w(0,0)=w(0,1)=w(1,0)=1,w(1,1)=-1\)
对于更高维度的情况
-
不妨定义 \(\&\) 为每个维度取 \(\min\) 之后的运算结果
则 \(w(i,j)w(i,k)=w(i,j\&k)\),到每一位,也即是 \(w_t(i_t,j_t)w_t(i_t,k_t)=w_t(i_t,\min(j_t,k_t))\)
可以构造矩阵(以三维为例)
\(w_t(x,y)=[x\le y]\)
当然分治的时候还是将其按照最高位的值拆掉,然后将仅最高位不同的这些位置拿出来乘 \(w_t\) 即可。
-
定义高维异或指不进位加法
则 \(w_t(i_t,j_t)w_t(i_t,k_t)=w_t(i_t,j_t+k_t\bmod K)\),其中 \(K\) 是维度。
这令我们想到单位根,因为单位根有 \(w^n_n=1\) 的优雅性质。
那么可以构造 \(w_t(i_t,j_t)=w^{j_t}_K\)
但是这不能够满足有逆,所以考虑构造 \(w_t(i_t,j_t)=w_{K}^{i_tj_t}\)
这个矩阵的逆?\(w^{-1}_t(i_t,j_t)=\frac{1}{K}w_t^{-i_tj_t}\)
模意义下就是原根。
因为 \(g^{P-1}\equiv 1\pmod P\),因此取 \(g^{\frac{P-1}{n}}\) 就可以了。
注意要求 \(n|P-1\)