2025.3.29日 清华大学-郝泽旭 的模拟赛

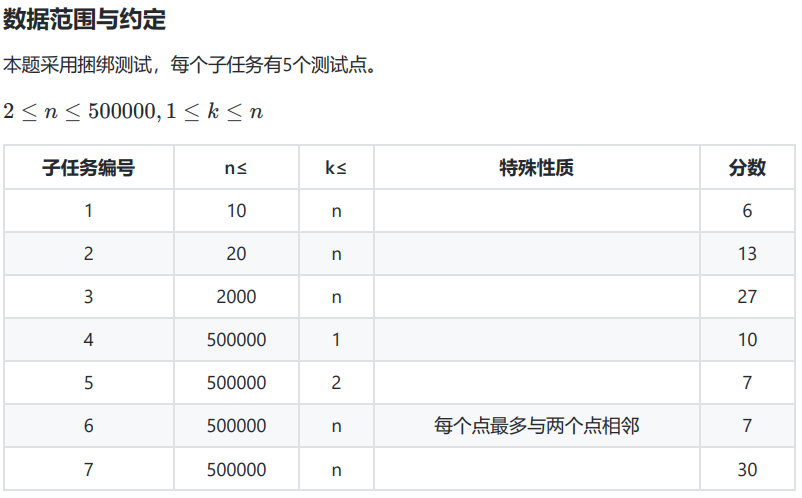
原题可以转化为给定了 \(k\) 个起点,求 \(k\) 个终点,使得路径两两无公共点的所有路径之和的最大值。
注意到先上再下的路径可以拆成两部分,即从关键点开始先向上到达一个点后再向下可以看作一条从关键点向上的路径与一条从非关键点向上的路径相合并。
于是设 \(dp_{u,0/1/2}\) 表示节点 \(u\) 处,下面连着一个关键点/下面连着一个非关键点/下面没有连点的方案数,即可转移。

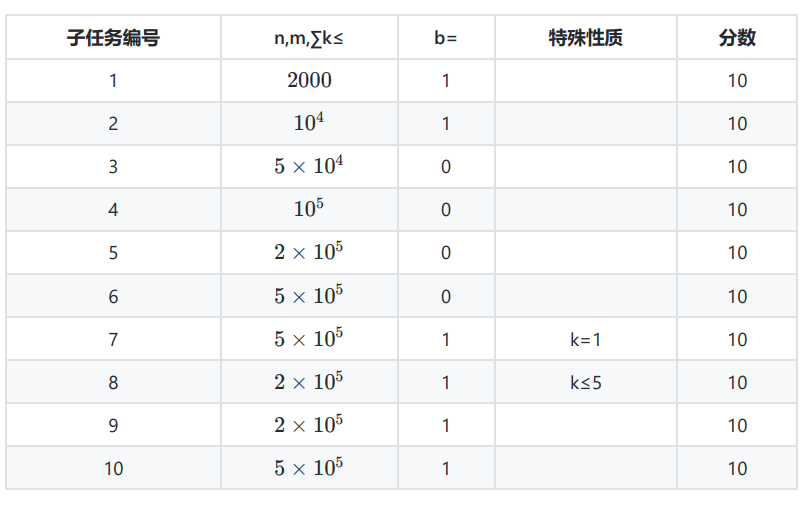
连通块个数是点数减边数。
现在就是要考虑总共包含了多少边数。先用dfn代替点的编号。
有一个做法是枚举每个点看其父亲节点在不在 \(S\) 中,单次复杂度 \(\mathcal O(n)\)。
有另一个做法是, 对于一条边 \((u,v),\exists i,j,u\in[l_i,r_i],v\in [l_j,r_j]\),那么这相当于是一个矩形,由于有 \(k\) 个区间,相当于是查询 \(k^2\) 个矩形中的点数,这用主席树做到单次 \(\mathcal O(k^2\log n)\)。
神奇的启发式,来啦!让我们聚在一起吧,说时迟,那时快,当 \(k^2\log n<n\) 时用算法二否则用算法一,则复杂度为
\[\max\sum_i \min(k_i^2\log n,n)
\]
又因为 \(\sum k\le n\),所以最后复杂度为 \(\mathcal O(n\sqrt{n\log n})\) 可以过 \(80\) 分。