高性能计算-GPU并行扫描

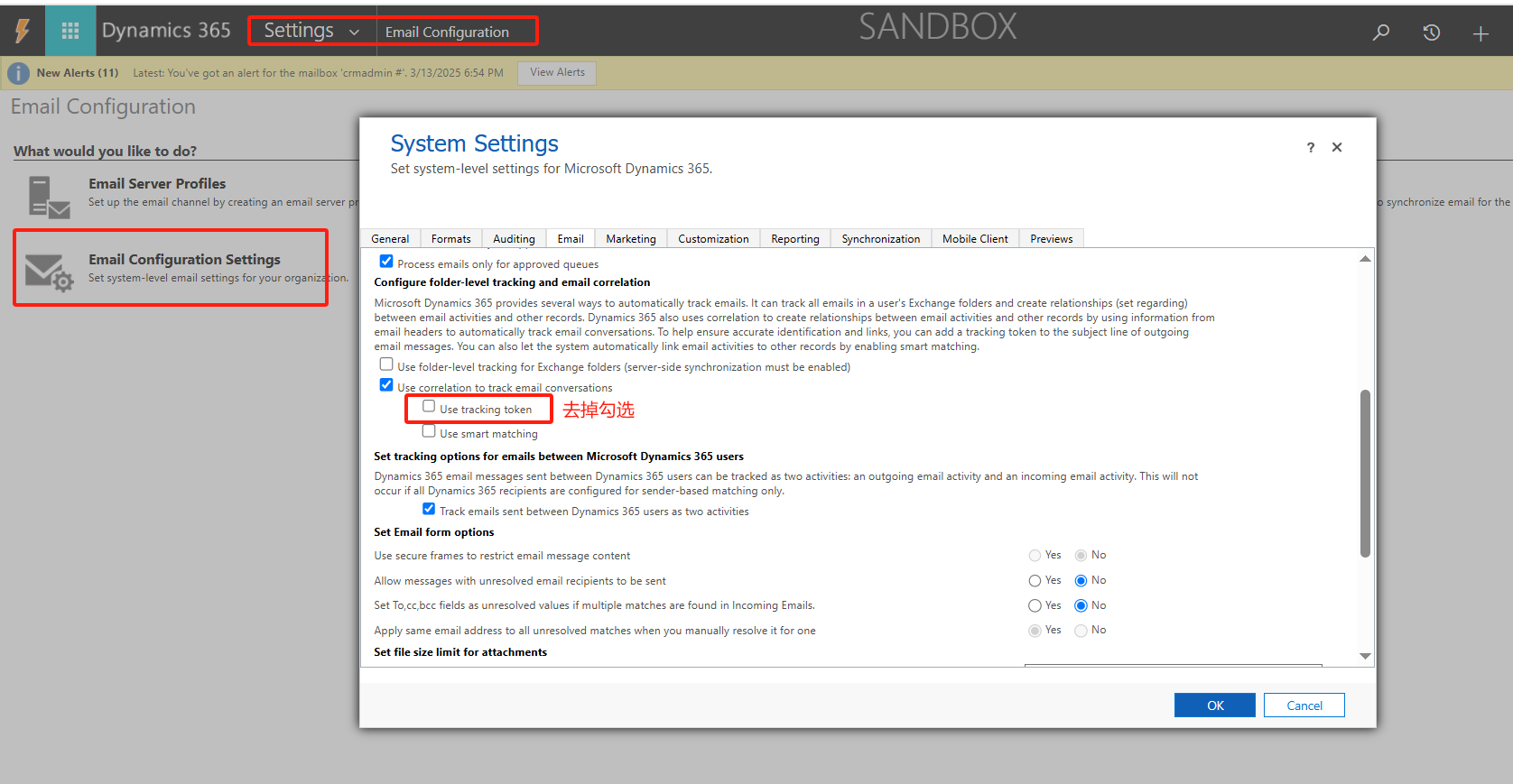
1. 扫描概念

• 对数组arr[N]扫描就是得到数组prefix[N]，每个元素是之前arr元素的求和.
• 开扫描定义:prefix1[N] = { arr[0], arr[0]+arr[1], ..., arr[0]+arr[1]+arr[N-1] }
• 闭扫描定义: prefix2[N] = { 0, arr[0], arr[0]+arr[1], ..., arr[0]+arr[1]+arr[N-12}

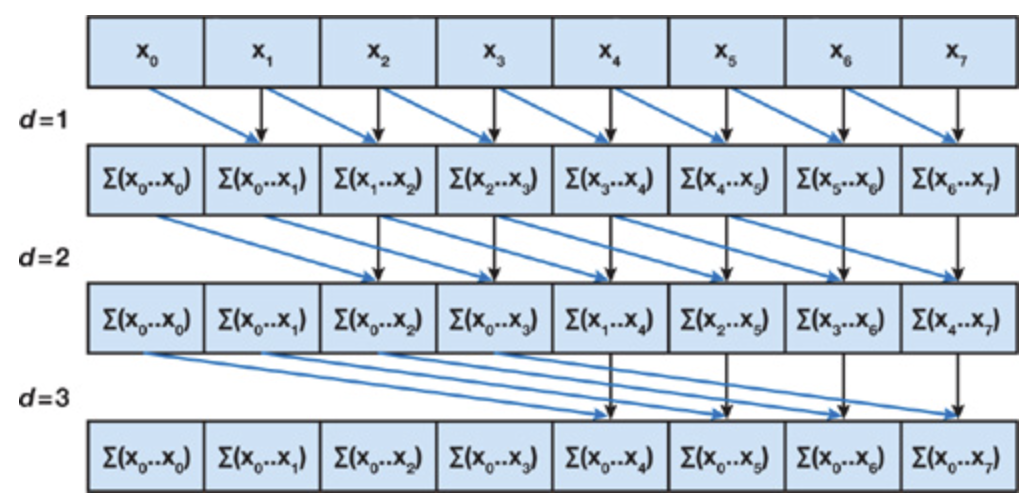
2. Hillis steele 扫描算法

（1）一种闭扫描算法。基础的Hillis steele 扫描算法只能扫描单块，步骤复杂度为 O(logN)，计算复杂度为 O(N*logN).
（2）基础版算法介绍：假设步长为s每次迭代 >=s的线程参与计算，本线程id作为被加数，往前 -s 索引为加数

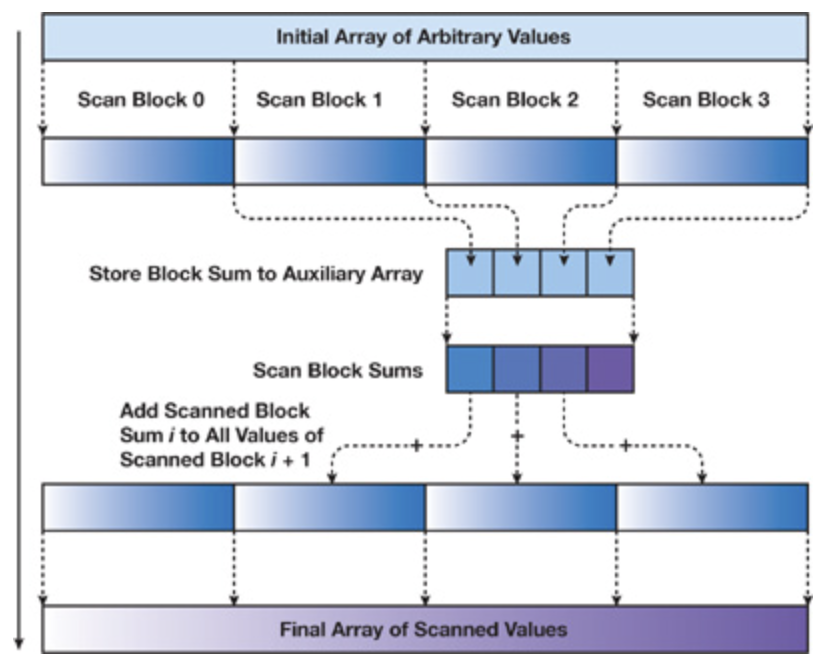
（3）支持任意block倍数长度的数据输入，介绍：

a) 扫描block：按blocksize划分数据，每个block处理一个数据块，块内进行扫描，输出前缀和和块内求和结果辅助数组
b) 递归扫描辅助数组：递归为了将块内求和辅助数组的结果加到块内扫描结果上，需要扫描辅助数组，如果辅助数组大于256那么要考虑辅助数组递归扫描；直到辅助数组被扫描求和数组block为1，扫描结束，反向依次弹栈把求和数组加到对应前缀数组上。

（4）优化：共享内存使用双buffer，读写分离，避免读写 bank冲突
（5）代码：

/*
任意长度扫描,单块扫描使用Hillis Steele算法,使用double buffer避免读写bank冲突;默认输入数据长度是blockSize的倍数
*/#include "common.h"
#include <stdio.h>#define BlockSize 512//单块扫描函数, in 输入数据, out 扫描结果, len1 扫描数据长度,sum block求和数组,len2 sum数组大小
__global__ void kernel_BlockScan(int *in,int * out,int len1,int *sum,int len2)
{//取单块数据到共享内存,使用双buffer,读写分离,避免读写bank冲突__shared__ int arrShared[2*BlockSize];int bid = blockIdx.x;   //块idint tid = blockIdx.x * blockDim.x + threadIdx.x;    //全局线程idint tbid = threadIdx.x; //块内线程idint write = 0;  //初始化第0个buff writeint read = 1;   //初始化第1个buff readif(tid<len1){//共享内存read buffer数据初始化arrShared[read*BlockSize + tbid] = in[tid]; __syncthreads();for(int s=1;s<BlockSize;s<<=1){// Hillis Steele算法:索引大于步长的线程参与计算,对应位置上的倍加数+块内前面步长位置的加数if(tbid>=s){//被加数索引int id = read*BlockSize + tbid;arrShared[write*BlockSize + tbid] = arrShared[id] + arrShared[id -s]; }else//否则保留上一轮计算的前缀和arrShared[write*BlockSize + tbid] = arrShared[read*BlockSize + tbid];//每循环一次,读写buffer区域交换__syncthreads();write = 1 - write;read = 1- read;}// 将block计算结果赋值给outout[tid] = arrShared[read*BlockSize + tbid];//将块内求和按块索引号放求和数组if(tbid==(BlockSize-1))sum[bid] = arrShared[read*BlockSize + tbid];}
}//对第一轮扫描结果后处理函数,len 数据总长度
__global__ void handPost(int* first,int len,int *second)
{int tid = blockDim.x * blockIdx.x + threadIdx.x;int bid = blockIdx.x;int tbid = threadIdx.x; //块内线程id//从第二块开始加上前一个块的sum值if(bid>0 && tid<len){//取出被加数__shared__ int temp;if(tbid==0)temp = second[bid-1];__syncthreads();first[tid] += temp;}
}//输入分块扫描分配及后处理函数,输出结果的空间在外面分配
//这里第一二轮扫描都使用该函数递归调用,n输入数据长度
void scan(int *in,int *arrResult,int n)
{int GridSize = (n-1)/BlockSize + 1;printf("gridSize:%d\n",GridSize);int *arrResultFirstSum;CudaSafeCall(cudaMalloc((void**)&arrResultFirstSum,GridSize*sizeof(int)));kernel_BlockScan<<<GridSize,BlockSize,2*BlockSize*sizeof(int)>>>(in,arrResult,n,arrResultFirstSum,GridSize);CudaCheckError();//循环扫描递归终止条件:假如第一次扫描gridsize=4096大于256,组要循环扫描到 gridsize==1,block的和需要被handpost处理累加到后面if(GridSize==1){cudaFree(arrResultFirstSum);return;}//递归扫描:对本轮计算结果和的数组进行扫描int *arrResultSecond;//cudaMalloc 隐式同步CudaSafeCall(cudaMalloc((void**)&arrResultSecond,GridSize*sizeof(int)));scan(arrResultFirstSum,arrResultSecond,GridSize);//空流核函数隐式同步// cudaDeviceSynchronize();//将本轮扫描结果数组的索引+1作为第一次扫描结果按blockIdx.x的索引作为块内扫描结果的加数,得到最终扫描结果arrResulthandPost<<<GridSize,BlockSize,sizeof(int)>>>(arrResult,n,arrResultSecond);CudaCheckError();//cudafree是隐式同步CudaSafeCall(cudaFree(arrResultFirstSum));CudaSafeCall(cudaFree(arrResultSecond));return;
}int main(int argc ,char** argv)
{int N = 1<<20; //数据规模if(argc>1)N = 1 << atoi(argv[1]);//cpu串行计算int *arrHost = (int*)calloc(N,sizeof(int));int *resultHost = (int*)calloc(N,sizeof(int));int *resultFD = (int*)calloc(N,sizeof(int));float cpuTime = 0.0;initialDataInt(arrHost,N);double start = cpuSecond();//闭扫描//初始化第一个元素,避免循环内有判断,cpu分支预测错误resultHost[0] = arrHost[0];for(int i=1;i<N;i++)resultHost[i] = resultHost[i-1] + arrHost[i]; double end = cpuSecond();cpuTime = (end - start)*1000;//gpu计算int *arrD;int *resultD;float gpuTime = 0.0;CudaSafeCall(cudaMalloc((void**)&arrD,N*sizeof(int)));CudaSafeCall(cudaMalloc((void**)&resultD,N*sizeof(int)));cudaEvent_t startD,endD;CudaSafeCall(cudaEventCreate(&startD));CudaSafeCall(cudaEventCreate(&endD));CudaSafeCall(cudaMemcpy(arrD,arrHost,N*sizeof(int),cudaMemcpyHostToDevice));cudaEventRecord(startD);scan(arrD,resultD,N);CudaCheckError();cudaEventRecord(endD);cudaEventSynchronize(endD);CudaSafeCall(cudaMemcpy(resultFD,resultD,N*sizeof(int),cudaMemcpyDeviceToHost));cudaEventElapsedTime(&gpuTime,startD,endD);cudaEventDestroy(startD);cudaEventDestroy(endD);//结果比对checkResultInt(resultHost,resultFD,N);free(arrHost);free(resultHost);free(resultFD);CudaSafeCall(cudaFree(arrD));CudaSafeCall(cudaFree(resultD));printf("数据规模 %d kB,cpu串行耗时 %.3f ms ;gpu 单个block使用Hillis Steele 扫描(double buffer)计算耗时 %.3f ms,加速比为 %.3f .\n",N>>10,cpuTime,gpuTime,cpuTime/gpuTime);return 0;
}

3. Blelloch扫描算法

（1）一种开扫描算法。基础的 Blelloch扫描算法，只能处理单块数据。步骤复杂度为 O(2logN)，计算复杂度为 O(2LogN)。
（2）基础版算法介绍：

a) 规约：对块进行规约，每次循更新计算结果的位置的数值，其他数值不变。

b) 清零:迭代
c) 散出：迭代