---

引言

本系列为 CMU 15-445 Fall 2022 Database Systems 数据库系统 [卡内基梅隆] 课程重点知识点摘录，附加个人拙见，同样借助CMU 15-445课程内容来完成MIT 6.830 lab内容。

---

上节提到，DBMS 使用一些特定的数据结构来存储信息：

• Internal Meta-data
• Core Data Storage
• Temporary Data Structures
• Table Indexes

本节将介绍存储 table index 最常用的树形数据结构：B+ Tree，Skip Lists，Radix Tree

---

Table Index

table index 为提供 DBMS 数据查询的快速索引，它本身存储着某表某列排序后的数据，并包含指向相应 tuple 的指针。

DBMS 需要保证表信息与索引信息在逻辑上保持同步。用户可以在 DBMS 中为任意表建立多个索引，DBMS 负责选择最优的索引提升查询效率。但索引自身需要占用存储空间，因此在索引数量与索引存储、维护成本之间存在权衡。

---

B+ Tree

B-Tree Family

B-Tree 中的 B 指的是 Balanced，实际上 B-Tree Family 中的 Tree 都是 Balanced Tree。B-Tree 就是其中之一，以之为基础又衍生出了 :

B-Tree 与 B+ Tree 最主要的区别有以下几点:

• 节点结构:
  • B-Tree 的每个节点既包含索引键值，也包含数据。因此，节点的大小会相对较大，通常需要占用一页或多页的存储空间。
  • B+ Tree 的每个节点只包含索引键值，而数据则只保存在叶子节点上。因此，索引节点的大小会相对较小，通常只需要占用一部分存储页面即可。这样做可以提高内存缓存的命中率，从而加速索引查询和范围扫描等操作。
• 叶子节点的指针：
  • 在 B-Tree 中，每个叶子节点都包含了对应的数据项；而在 B+ Tree 中，叶子节点只包含对应的数据项，不含其他的指针信息。
  • 为了支持范围查找等操作，B+ Tree 的叶子节点之间通常会使用链表连接起来，形成一个有序的数据块。
• 索引查询
  • 在 B-Tree 中，每个非叶子节点都可能包含对应子树的数据项。因此，在进行索引查询时，可能需要通过递归遍历整棵树来定位目标数据项。这样做会导致频繁的 IO 访问和 CPU 开销，降低查询性能。
  • 而在 B+ Tree 中，非叶子节点只包含对应的键值，并且所有的数据项都保存在叶子节点上。因此，在进行索引查询时，可以通过快速定位到对应的叶子节点，并在其中进行顺序查找，从而减少 IO 访问和 CPU 开销，提高查询性能。

综上所述，B+ Tree 相比于 B-Tree 更适合用于磁盘存储和范围查询等场景，能够更好地利用内存缓存和硬件资源，优化查询性能和吞吐量。

• The original B-Tree from 1972 stored keys + values in all nodes in the tree.
  • More space efficient since each key only appears once in the tree.
• B+Tree only stores values in leaf nodes. Inner nodes only guide the search process.

---

B+ Tree

B+ Tree 是一种自平衡树，它将数据有序地存储，且在 search、sequential access、insertions 以及 deletions 操作的复杂度上都满足 O(logn)，其中 sequential access 的最终复杂度还与所需数据总量有关。

B+ Tree 可以看作是 BST (Binary Search Tree) 的衍生结构，它的每个节点可以有多个 children，这特别契合 disk-oriented database 的数据存储方式，每个 page 存储一个节点，使得树的结构扁平化，减少获取索引给查询带来的 I/O 成本。其基本结构如下图所示：

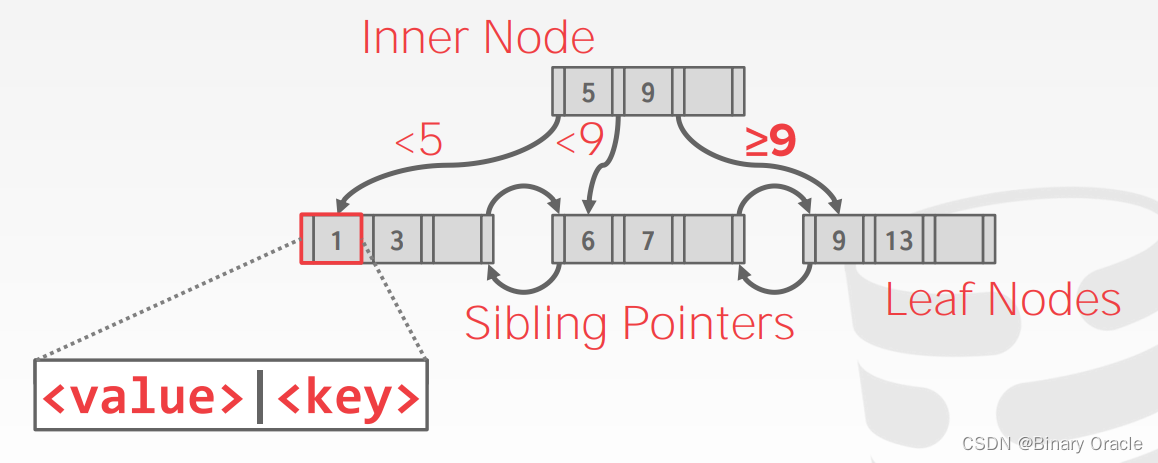
以 M-way B+tree 为例，它的特点总结如下：

• 每个节点最多存储 M 个 key，有 M+1 个 children
• B+ Tree 是 perfectly balanced，即每个 leaf node 的深度都一样
• 除了 root 节点，所有其它节点中至少处于半满状态，即 M/2−1≤#keys≤M−1
• 假设每个 inner node 中包含 k 个 keys，那么它必然有 k+1 个 children
• B+ Tree 的 leaf nodes 通过双向链表串联，从而为 sequential access 提供更高效的支持

---

B+ Tree Nodes

B+ Tree 中的每个 node 都包含一列按 key 排好序的 key/value pairs，key 就是 table index 对应的 column，value 的取值与 node 类型相关，在 inner nodes 和 leaf nodes 中存的内容不同。

leaf node 的 values 取值在不同数据库中、不同索引优先级中也不同，但总而言之，通常有两种做法：

• Record/Tuple Ids：存储指向最终 tuple 的指针
• Tuple Data：直接将 tuple data 存在 leaf node 中，但这种方式对于 Secondary Indexes 不适用，因为 DBMS 只能将 tuple 数据存储到一个 index 中，否则数据的存储就会出现冗余，同时带来额外的维护成本。

此外，leaf node 还需要存储相邻 siblings 的地址以及其它一下元信息，如下图所示：

---

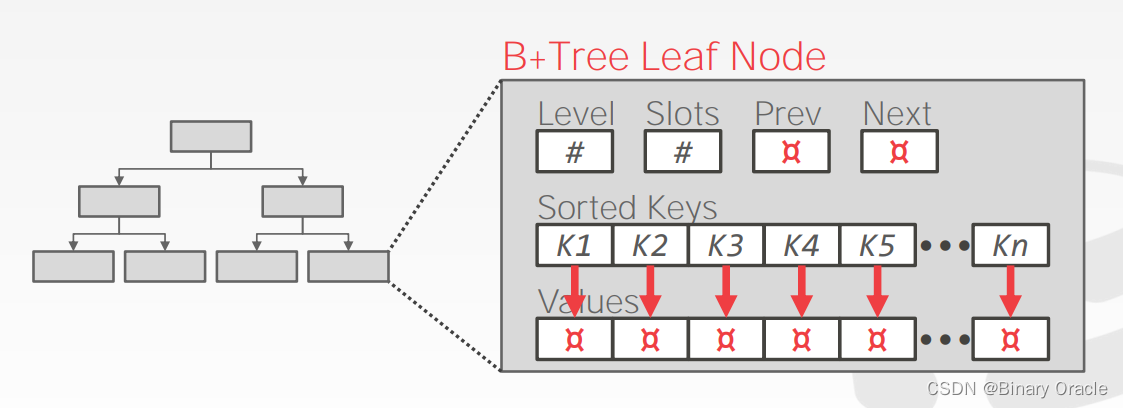
B+ Tree Operations

Insert

1. 找到对应的 leaf node，L
2. 将 key/value pair 按顺序插入到 L 中
3. 如果 L 还有足够的空间，操作结束；如果空间不足，则需要将 L 分裂成两个节点，同时在 parent node 上新增 entry，若 parent node 也空间不足，则递归地分裂，直到 root node 为止。

Delete

1. 从 root 开始，找到目标 entry 所处的 leaf node, L
2. 删除该 entry
3. 如果 L 仍然至少处于半满状态，则操作结束；否则先尝试从 siblings 那里拆借 entries，如果失败，则将 L 与相应的 sibling 合并
4. 如果合并发生了，则可能需要递归地删除 parent node 中的 entry

B+Tree 的 Insert、Delete 过程，可参考这里。

---

In Practice

综合上面数据能够得出的结论:

填充因子:

• 平均扇出数计算公式

average fanout = 2 * degree * fill-factor

• 对于 B+ 树来说，通常选取 67% 的填充因子。基于这个填充因子，可以计算出平均分支数（average fanout）为 134。
  • 结论是，由于 B+ 树每个节点中包含的键值对数量较多，在设计和优化 B+ 树索引时，需要在平衡树高度和节点大小之间找到一个合适的折中方案。通过选择合适的填充因子，可以在保持树高度较小的同时，尽量减少节点大小和浪费空间。而平均分支数则是衡量 B+ 树查询性能和存储效率的重要指标之一，表示每个非叶子节点所能容纳的子节点数量的期望值。在实际应用中，通常会将平均分支数控制在一定范围内，以获得更好的查询性能和空间利用率。

空间占用:

• 在 B+ 树中，当树高度分别为 4 和 3 时，可以容纳的索引项数量分别为 312,900,721 和 2,406,104 (本例中)。

每一层级的Page:

• B+ 树索引的存储空间会随着树的高度增加而线性增长。例如，在这里给出的计算中，当 B+ 树高度为 3 时，需要的存储空间就达到了 140 MB，相比之下，一级索引只需要 8 KB 的存储空间。
• 针对不同层级的索引，需要选择合适的存储介质和访问方式。例如，一级索引通常可以直接保存在内存中，以快速响应查询请求；而高层级的索引则可能需要使用磁盘或其他辅助存储设备，并通过预读或批量操作等方式减少 IO 访问次数和延迟。
• 在实际应用中，需要根据数据特征、查询模式、硬件配置和成本效益等多种因素进行权衡和优化。例如，可以通过调整节点大小、填充因子、分裂策略等方式来控制 B+ 树的高度和存储空间，以满足不同的性能需求和存储容量限制。

---

Clustered Indexes

Clustered Indexes 规定了 table 本身的物理存储方式，通常即按 primary key 排序存储，因此一个 table 只能建立一个 cluster index。有些 DBMSs 对每个 table 都添加聚簇索引，如果该 table 没有 primary key，则 DBMS 会为其自动生成一个；而有些 DBMSs 则不支持 clustered indexes。

---

Compound Index

DBMS 支持同时对多个字段建立 table index（B+ Tree），即 compound index，如:

CREATE INDEX compound_idx ON table (a, b, c);

它可以被用在包含 a 的 condition 的查询中，如：

SELECT cFROM tableWHERE a = 5 AND b >= 42 AND c < 77;SELECT cFROM tableWHERE a = 5 AND b >= 42;SELECT cFROM tableWHERE a = 5;

尽管它可以被用在不包含 a 相关 condition 的查询中，但这约等于全表扫描，因此 DBMS 通常会使用全表扫描。如果使用 hash index 作为 table index，则必须对 (a, b, c) 完全匹配才可以使用。

---

B+ Tree Design Choices

Node Size

通常来说，disk 的数据读取速度越慢，node size 就越大：

Disk Type	Node Size
HDD	~1MB
SSD	~10KB
In-Memory	~512B

具体情境下的最优大小由 workload 决定。

Merge Threshold

• 在 B+ 树的插入和删除操作中，如果某个节点的填充因子下降到一个阈值以下（通常是一半），就需要触发节点合并或者数据搬迁等重组操作，以恢复平衡性质。然而，频繁的节点合并和分裂操作会导致大量的 IO 访问和锁竞争，从而影响查询性能和并发度。
• 为了减少这种代价，一些 DBMS 采用了一种优化策略，即延迟节点合并操作，直到节点填充因子降到一个更低的阈值（比如四分之一）。这样可以减少节点抖动（shaking）现象，即频繁地在相邻节点之间进行数据转移，从而提高索引的稳定性和可靠性。
• 另外，一些 DBMSs 还采用了周期性重建（rebuild）B+ 树的策略，即定期对整棵树进行重建，以消除节点空洞、碎片和过多的层级等问题。尽管这种策略会造成一定的停机时间和资源浪费，但可以有效地减少维护和调整索引的代价，并且有利于优化查询性能和工作负载的变化。

Variable Length Keys

B+ Tree 中存储的 key 经常是变长的，通常有三种手段来应对：

1. Pointers：存储指向 key 的指针
2. Variable Length Nodes：需要精细的内存管理操作
3. Key Map：内嵌一个指针数组，指向 node 中的 key/val list

Non-unique Indexes

索引针对的 key 可能是非唯一的，通常有两种手段来应对：

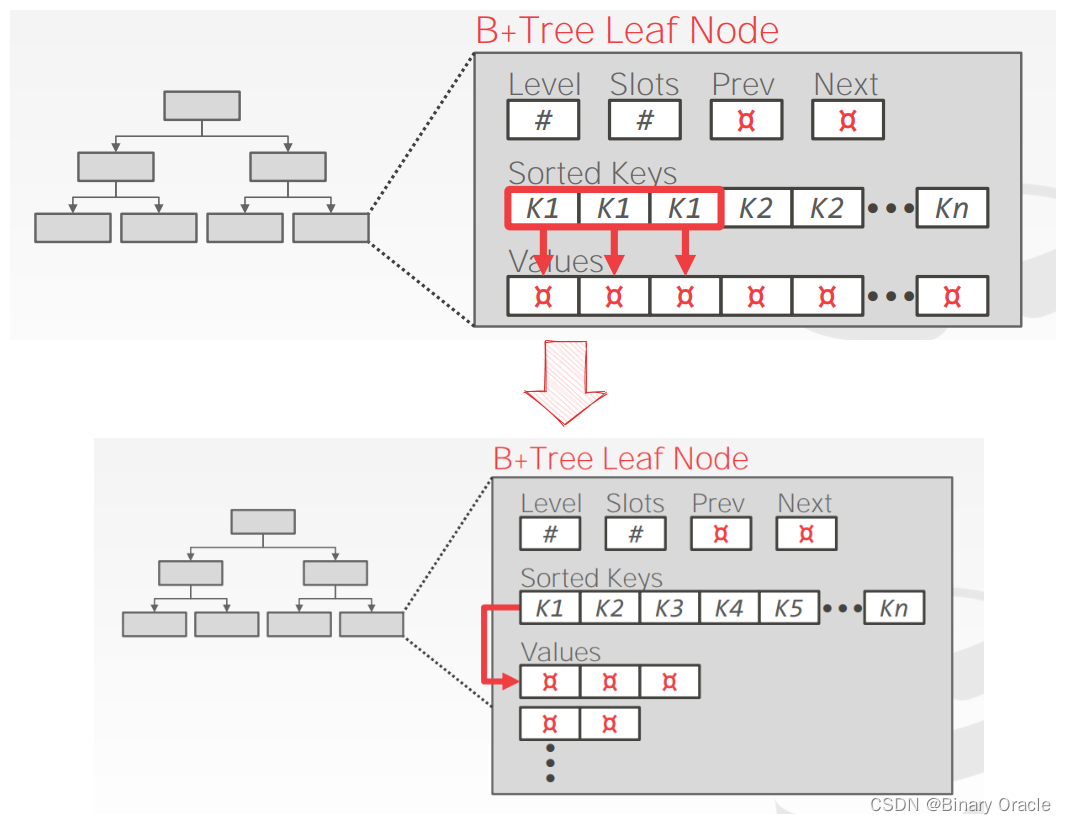
1. Duplicate Keys：存储多次相同的 key

2. Value Lists：每个 key 只出现一次，但同时维护另一个链表，存储 key 对应的多个 values，类似 chained hashing

分别如下面两张图所示：

Intra-node Search

在节点内部搜索，就是在排好序的序列中检索元素，手段通常有：

• Linear Scan
• Binary Search
• Interpolation：通过 keys 的分布统计信息来估计大概位置进行检索

---

Optimizations

Prefix Compression

同一个 leaf node 中的 keys 通常有相同的 prefix，如下图所示：

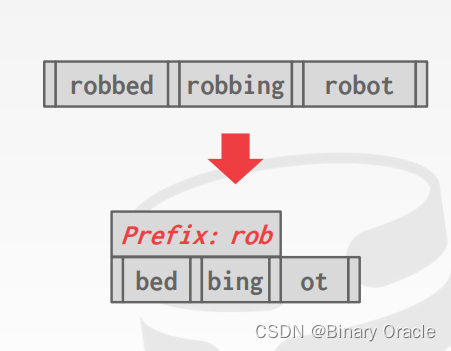
为了节省空间，可以只存所有 keys 的不同的 suffix。

---

Suffix Truncation

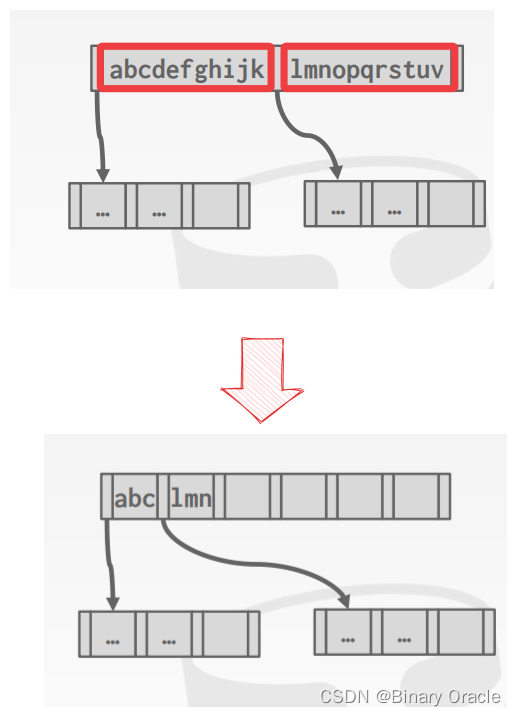
由于 inner nodes 只用于引导搜索，因此没有必要在 inner nodes 中储存完整的 key，我们可以只存储足够的 prefix 即可，如下图所示：

---

Bulk Insert

建 B+ Tree 的最快方式是先将 keys 排好序后，再从下往上建树，如下图所示：

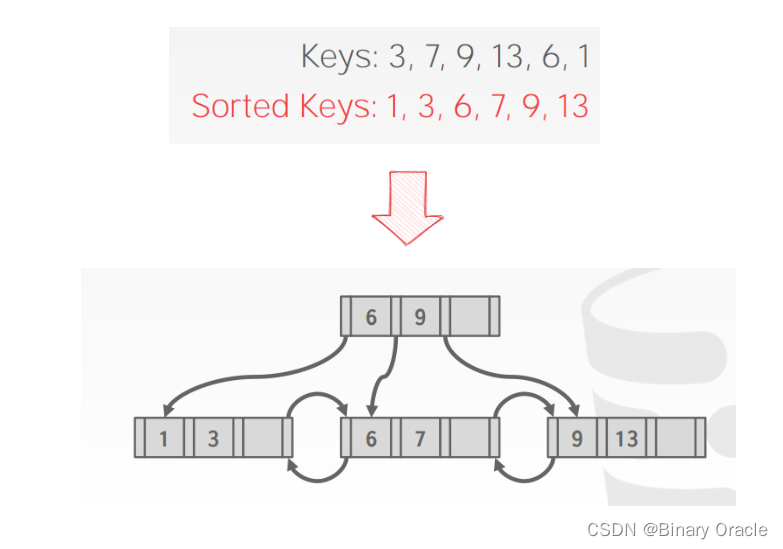
因此如果有大量插入操作，可以利用这种方式提高效率

---

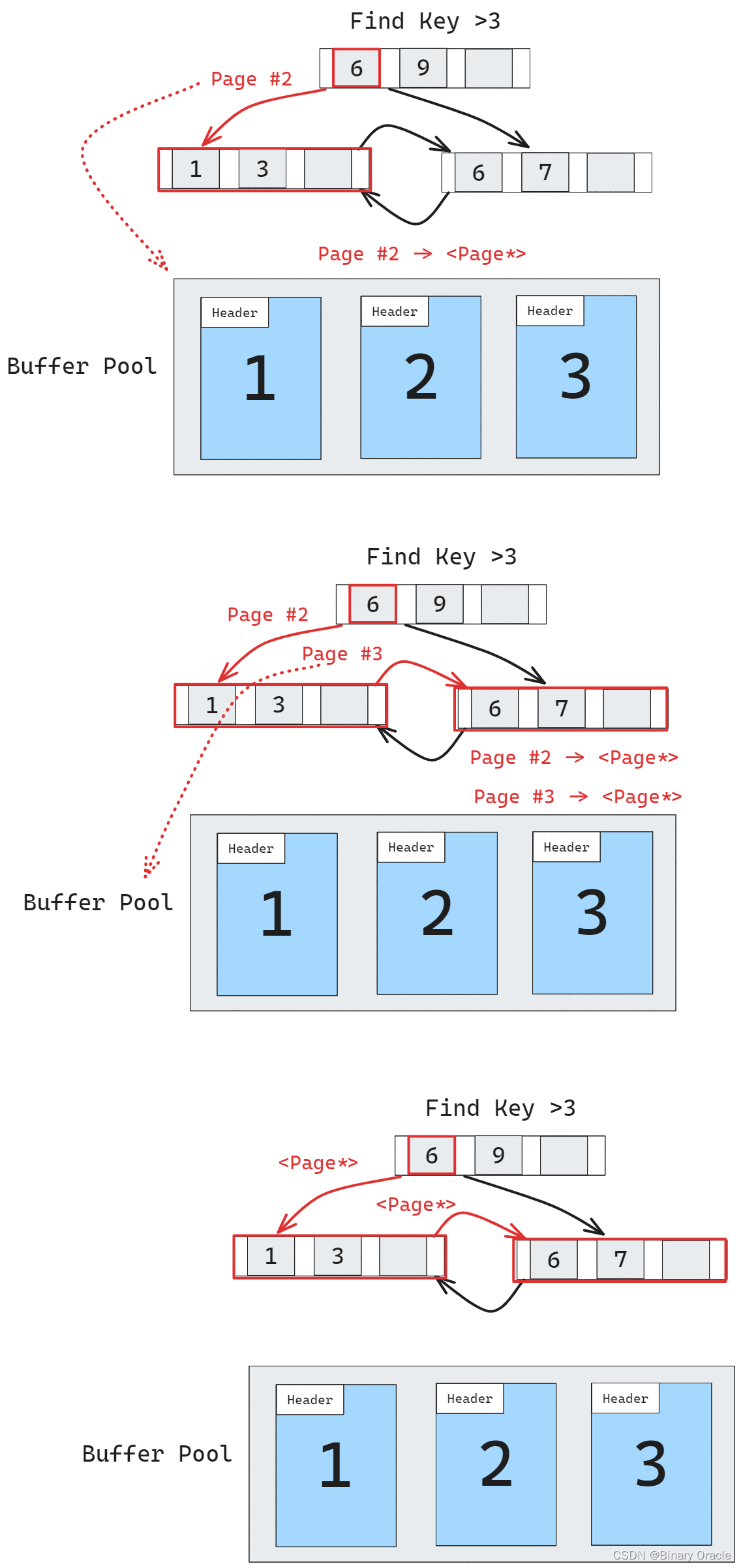
Pointer Swizzling（指针重定向）

Nodes 使用 page id 来存储其它 nodes 的引用，DBMS 每次需要首先从 page table 中获取对应的内存地址，然后才能获取相应的 nodes 本身，如果 page 已经在 buffer pool 中，我们可以直接存储其它 page 在 buffer pool 中的内存地址作为引用，从而提高访问效率。

---

Additional Index Usage

Implicit Indexes

许多 DBMSs 会自动创建 index，来帮助施行 integrity constraints(完整性约束)，情形包括：

• Primary Keys
• Unique Constraints
• Foreign Keys

如当我们创建下面的 foo table 时：

CREATE TABLE foo (id SERIAL PRIMARY KEY,val1 INT NOT NULL,val2 VARCHAR(32) UNIQUE
);CREATE TABLE bar (id INT REFERENCES foo (val1),val VARCHAR(32)
);

DBMS 可能会自动建立以下索引：

CREATE UNIQUE INDEX foo_pkey ON foo (id);        /* primary keys */
CREATE INDEX foo_val1_key ON foo (val1);         /* foreign keys */
CREATE UNIQUE INDEX foo_val2_key ON foo (val2);  /* Unique Constraints */

---

Partial Indexes

只针对 table 的子集建立 index，这可以大大减少 index 本身的大小，如下所示：

CREATE INDEX idx_fooON foo (a, b)WHERE c = 'WuTang';

一种常见的使用场景就是通过事件来为 indexes 分区，即为不同的年、月、日分别建立索引。

---

Covering Indexes

如果 query 所需的所有 column 都存在于 index 中，则 DBMS 甚至不用去获取 tuple 本身即可得到查询结果，如下所示：

CREATE INDEX idx_foo ON foo (a, b);SELECT b FROM fooWHERE a = 123;

甚至可以在 index 中有意加入别的 column （INDEX INCLUDE COLUMNS）：

CREATE INDEX idx_fooON foo (a, b)INCLUDE (c);

---

Functional/Expression Indexes

index 中的 key 不一定是 column 中的原始值，也可以是通过计算得到的值，如针对以下查询：

SELECT * FROM usersWHERE EXTRACT(dow FROM login) = 2;

直接针对 login 建立索引是没用的，这时候可以针对计算后的值建立索引：

CREATE INDEX idx_user_login ON users (EXTRACT(dow FROM login));

---

SkipList

从上文的介绍中，可以发现 table index 实际上就是一个 dynamic order-preserving 的数据结构，同时对增删改查的操作应提供较高的性能（B+ Tree，O(log n) ）。

dynamic order-preserving 的数据结构中，最简单的就是 sorted linked list，所有操作的复杂度均在 O(n) ，性能较 B+ Tree 相比逊色许多，但如果将多个 sorted linked list 垒起来，就可能提供与 B+ Tree 相媲美的性能。

Skip Lists 是一种随机数据结构（Randomized Data Structure），它是 Set (Ordered Set) 的一种实现。它的各操作复杂度如下表所示：

Operation Name	Time Complexity	Space Complexity
find-key(k)	O(lgn)	O(1)
iter()	O(n)	O(n)
insert(x)	O(lgn)	O(1)
delete-key(k)	O(lgn)	O(1)
delete-min/max()	O(lgn)	O(1)
find-next/prev(k)	O(lgn)	O(1)
find-min/max()	O(lgn)	O(1)
order-iter()	O(n)	O(1)

One Linked List：

当我们有一个 Linked List 时，Search 操作在最差情况下的复杂度为O(n)，我们有什么方式能够提高它的速度呢？

Two Linked Lists:

• 快速公交系统（BRT）与普通公交系统的区别在于：普通公交系统与其它私人交通工具共享车道且每站必停，而快速公交系统独享车道，且只经停部分公交站。那么假如我要从 A 地区 B 地（快速公交不可直达），就可以先从 A 开始乘坐快速公交到达离 B 最近的公交站，再乘坐普通公交到达 B。如果我们把 Search 操作比喻成这样的乘车过程，可以考虑使用两个 Linked Lists：
  

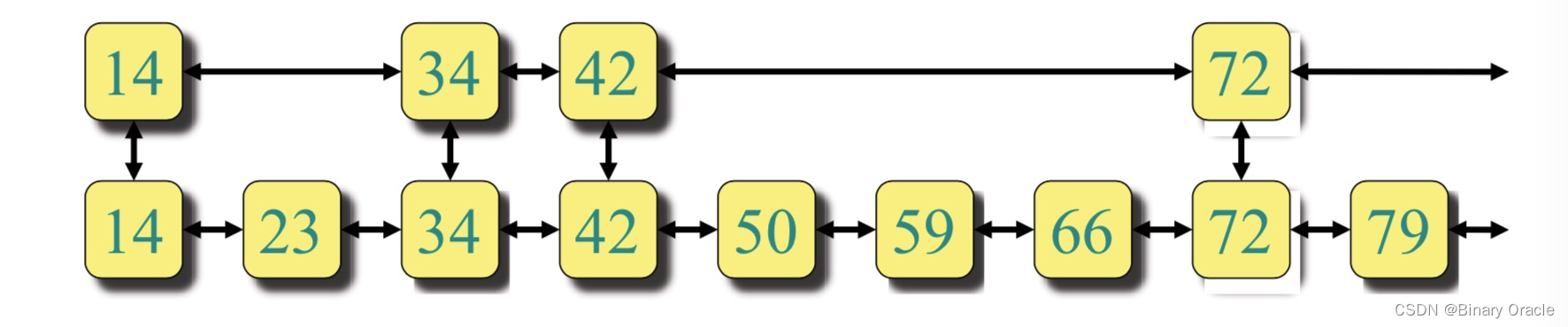
如图 2 所示，举例如下：

• 14 -> 59：14 -> 34 -> 42 -> 50 -> 59
• 14 -> 79：14 -> 34 -> 42 -> 72 -> 79

怎么设计快速公交系统的停靠站能使得公交系统的性能达到最大？直觉告诉我们，将快速公交的停靠站平均分布在普通公交停靠站上。那么这时候 Search 的成本为：

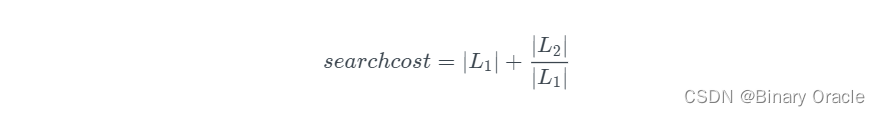
求其最小值，可以得到：

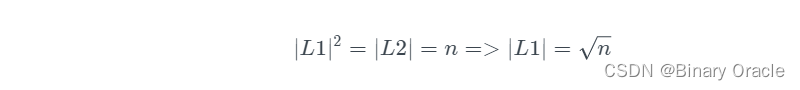
如此一来，Search 的成本就是：

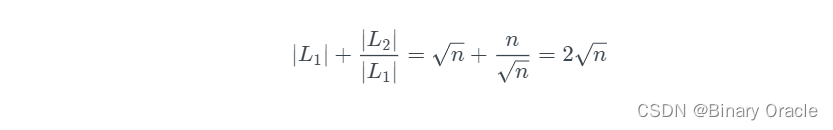
More Linked Lists：

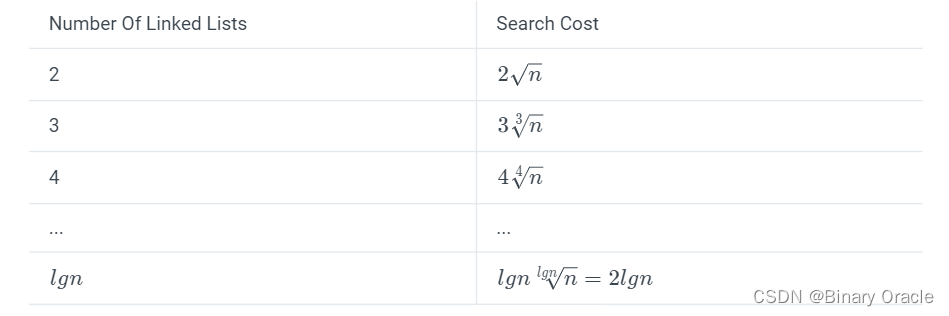
使用 个 linked lists 时，已经很像一棵树，如 B 树。

Skip Lists：

• 完美的 Skip Lists 就是由 lgn 个 linked lists 构成的数据结构。

---

Insert(x):

• 从空的 Skp Lists 开始不断 Insert 元素，就构成了 Skip Lists 的创建过程。如何保证这个过程能够建立出接近完美的 Skip Lists 其实就是 Insert 的实现需要解决的问题。
• 方案：先用 search/find 找到元素在最底层的位置，将元素插入到最底层中，然后以 1/2 的概率决定是否将该元素插入到上面一层，递归重复。根据概率理论，平均来看
  • 1/2 的元素会被插入到上面 0 层
  • 1/4 的元素会被插入到上面 1 层
  • 1/8 的元素会被插入到上面 2 层
  • …（以此类推）

search 的时间复杂度为O(lgn) ，递归插入的时间复杂度同样为O(lgn)，因此 insert 的总时间复杂度也为O(lgn)。

---

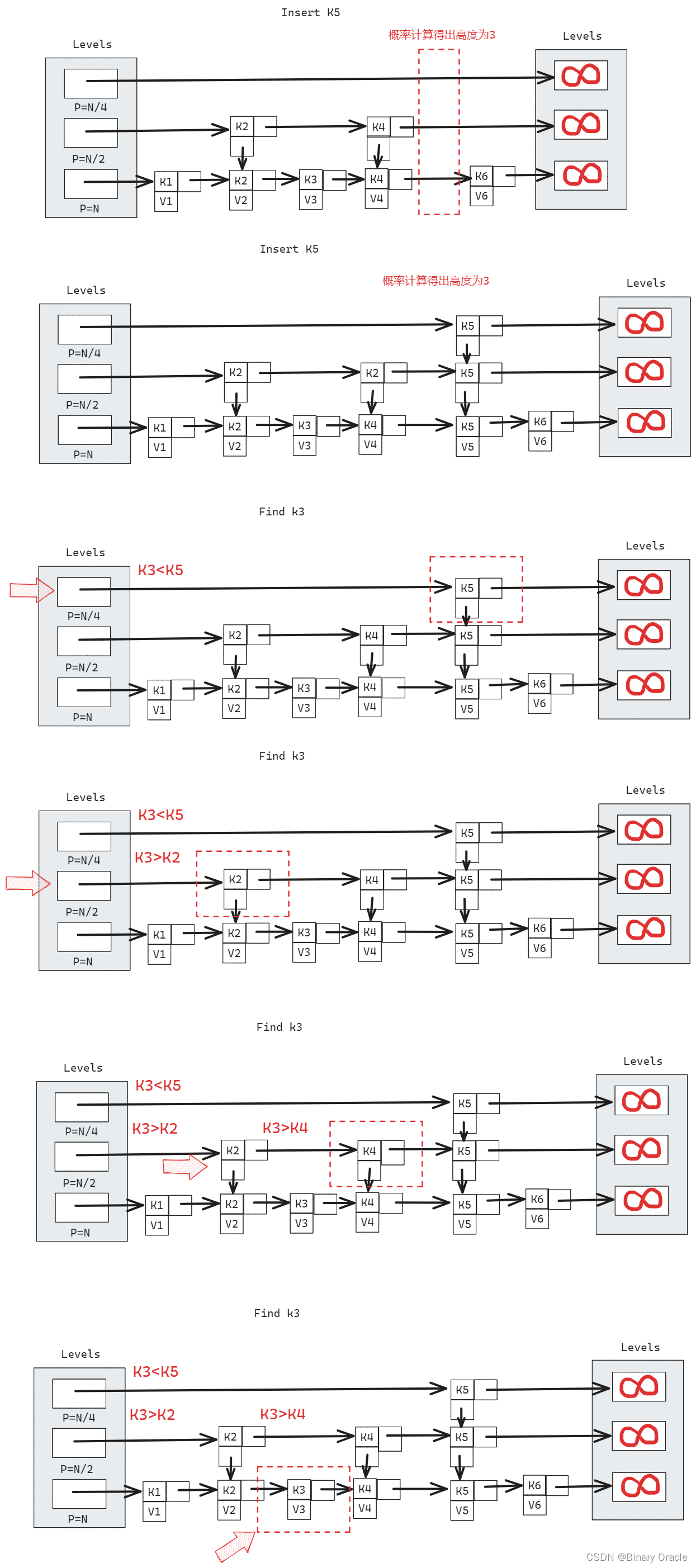
Delete(x):

• Delete 需要先用 search/find 找到元素的位置，然后从所有可能存在该元素的链表中删除该元素，因此总时间复杂度为O(lgn)。
• 具体证明请查阅参考资料。

---

Skip Lists 是一种基于概率的数据结构，它提供的复杂度都是期望的结果。它的 Pros & Cons 总结如下：

• Advantages
  • 比 B+ Tree 的一般实现使用更少的内存
  • 插入和删除操作不需要重新平衡树结构
• Disadvantages
  • 并不像 B+ Tree 一样对 disk/cache 的结构友好
  • 反向搜索实现复杂

---

Radix Tree（基数树）

Radix Tree vs. Trie:

• radix tree 实际上就是压缩后的 trie

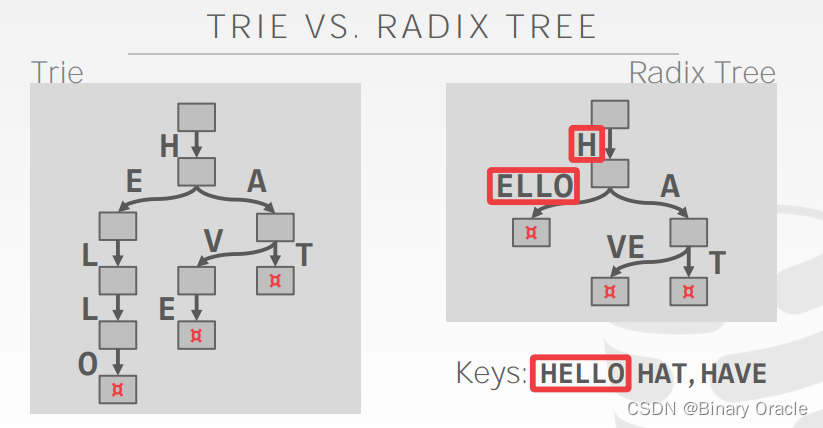
简介 --> radix tree 将每个 key 拆成一个序列：

• 树的高度取决于 keys 的长度
• 不需要重新平衡树（rebalancing）
• 从 root 到 leaf 的路径代表相应的 leaf

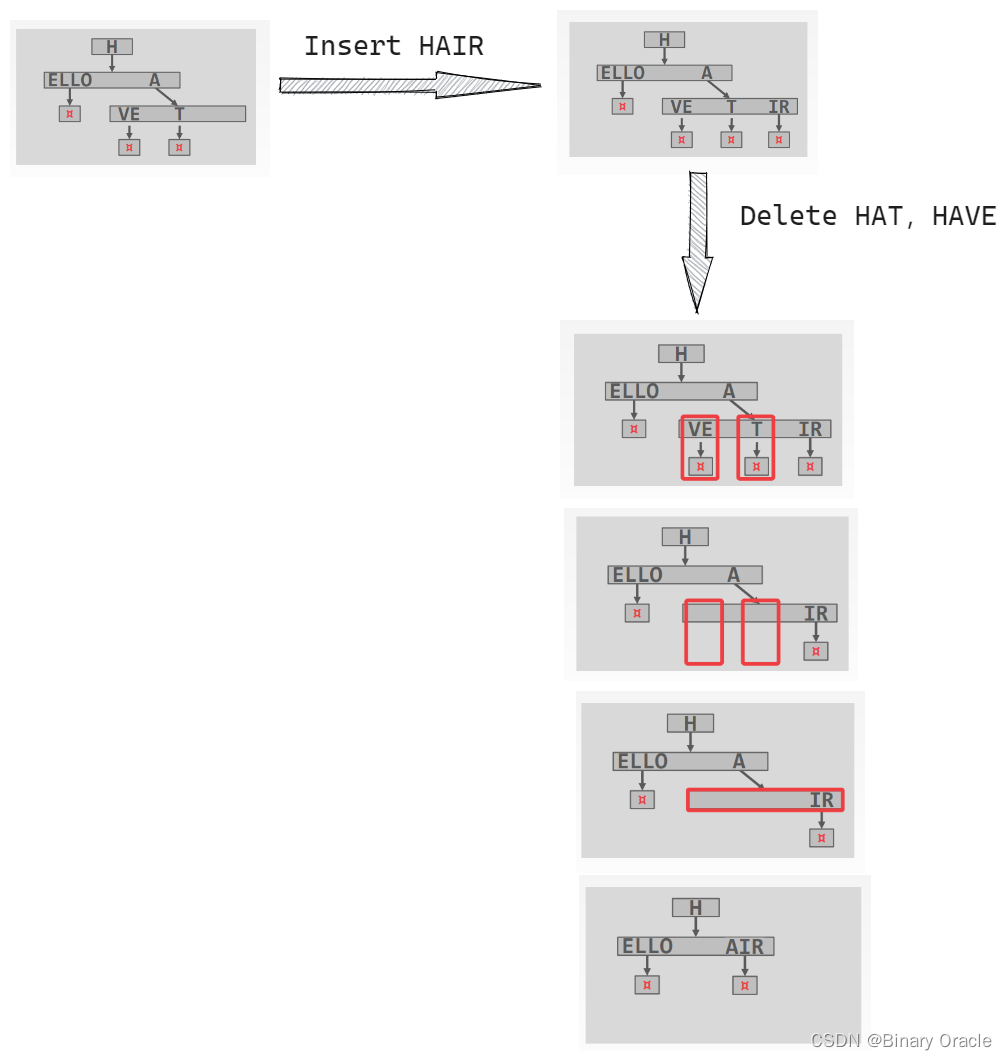
Binary Comparable Keys

为了让 keys 能够合理地拆解成序列，许多类型的 key 都需要特殊处理：

• Unsigned Integers：对小端存储的机器要把 bits 翻转一遍
• Signed Integers：需要翻转 2’s-complement 从而使得负数小于正数
• Floats：需要分成多个组，然后存储成 unsigned integer
• Compound：分别转化各个 attributes 然后组合起来

举例如下：

---

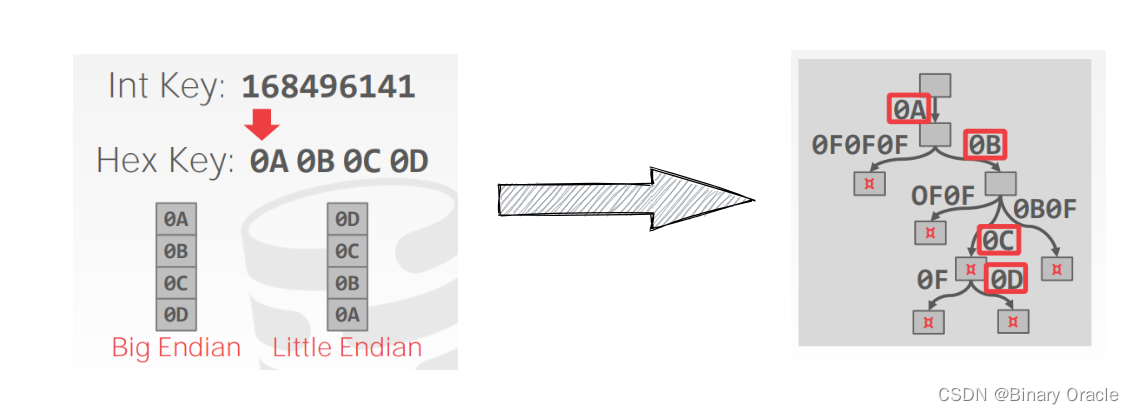
对比

---

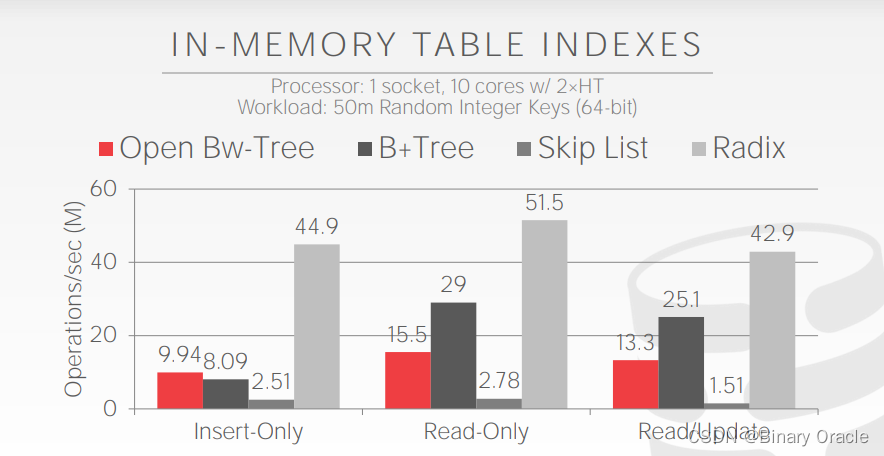
Inverted Indexes (倒排索引)

尽管 tree index 非常有利于 point 和 range 查询，如：

• Find all customers in the 15217 zip code
• Find all orders between June 2018 and September 2018

但对于 keyword search，tree index 就显得无能为力，如：

• Find all Wikipedia articles that contain the word “Pavlo”

尽管 DBMSs 在一定程度上支持这种搜索，但更复杂、灵活的查询就不是它们的专长。有一部分 DBMSs 专门提供复杂、灵活的 keyword search 功能，如 ElasticSearch、Solr、Sphinx 等。

Query Types

• Phrase Searches（短语搜索）：查找包含给定顺序的一组词语的记录。短语搜索用于寻找文档中连续出现的一组词语，这些词语按照给定的顺序出现。例如，如果我们搜索短语 “apple pie”，倒排索引将返回包含连续出现 “apple pie” 的文档。
• Proximity Searches（邻近搜索）：查找两个词语在彼此之间相隔 n 个单词的记录。邻近搜索用于查找文档中两个词语之间具有一定距离的情况。例如，如果我们进行邻近搜索 “apple” 和 “pie”，并将距离设置为 3，倒排索引将返回两个词语之间相隔不超过 3 个单词的文档。
• Wildcard Searches（通配符搜索）：查找包含与某种模式（例如正则表达式）匹配的词语的记录。通配符搜索用于在文档中查找与给定模式匹配的词语。通配符可以表示缺失的字符或字符序列，使搜索更加灵活。例如，如果我们搜索 “appl*”，倒排索引将返回包含以 “appl” 开头的词语（如 “apple”、“applies”）的文档。

这些高级搜索功能通过利用倒排索引中的词项表和倒排列表来实现。它们提供了更精确和灵活的搜索能力，以满足特定的查询需求，并在许多搜索引擎和数据库系统中被广泛使用。

---

如何设计

• 决策1：存储什么内容
  • 索引需要至少存储每个记录中包含的单词（由标点符号分隔）。这意味着在构建索引时，每个记录的文本应该被切分成单独的单词，并将这些单词与对应的记录标识一起存储在索引中。
  • 此外，您还可以存储额外的元数据，例如单词频率、位置或其他相关信息。这可以提供更高级的功能，例如根据单词频率对搜索结果进行排序，或通过存储单词位置来支持邻近搜索。
• 决策2：何时进行更新
  • 为了高效地更新索引，通常有利于维护辅助数据结构，以将更新操作分阶段并批量更新索引。而不是针对每个单独的记录修改立即更新索引，您可以将更新操作分批处理，然后批量执行它们。

通过使用暂存或缓冲机制，您可以将更新操作分阶段，将它们暂存起来，然后批量应用于索引。这种方式可以提高更新效率，并减少频繁地更新索引的开销。

---

小结

不管怎么说B+ Tree依然是Tree Indexes的首选，特殊的关键字搜索场景可以考虑倒排索引。

当然，本文不涉及地理空间树索引，例如R树（R-Tree）、四叉树（Quad-Tree）和KD树（KD-Tree），是用于组织和索引空间数据的数据结构。这些基于树的索引专门设计用于处理多维数据，通常用于表示和查询几何对象或空间坐标。

---

参考

教程对应的PPT上

教程对应的PPT下