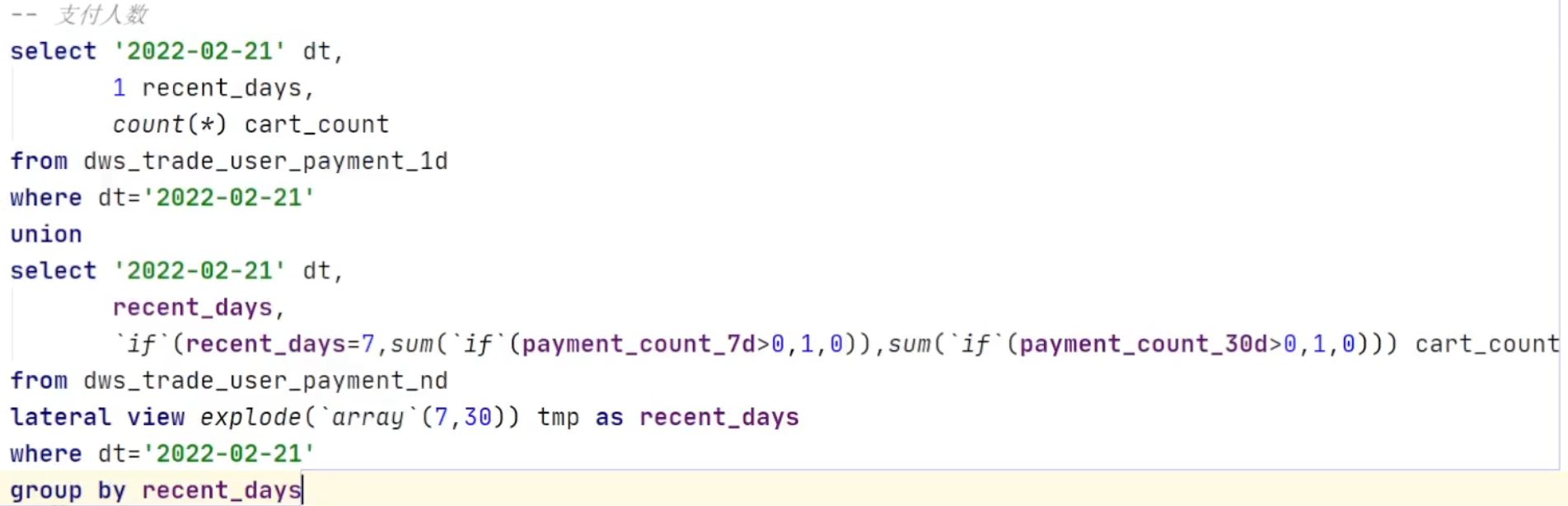
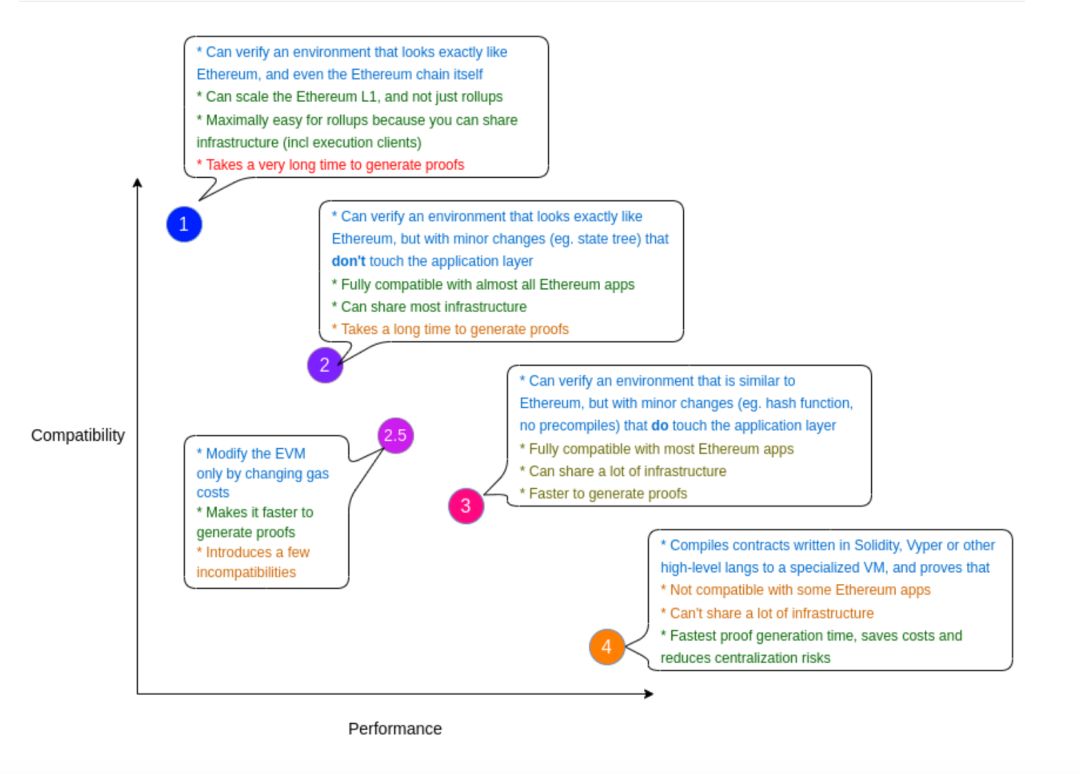
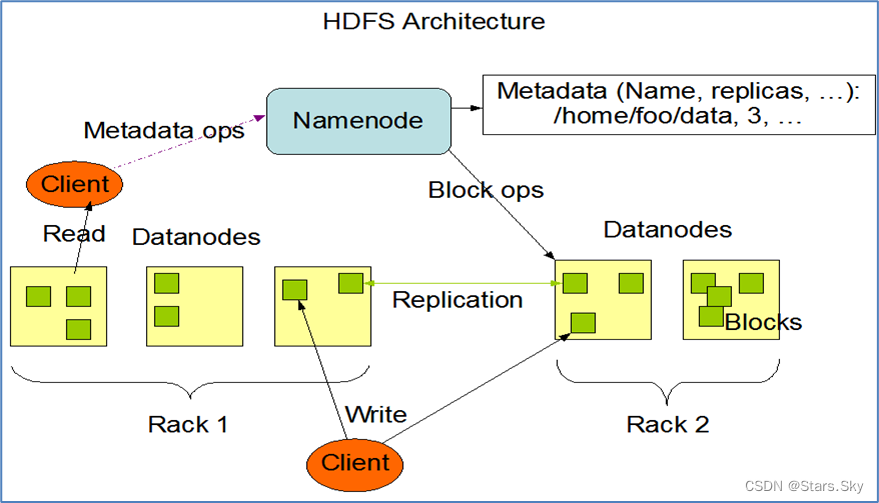
343.整数拆分
思路:
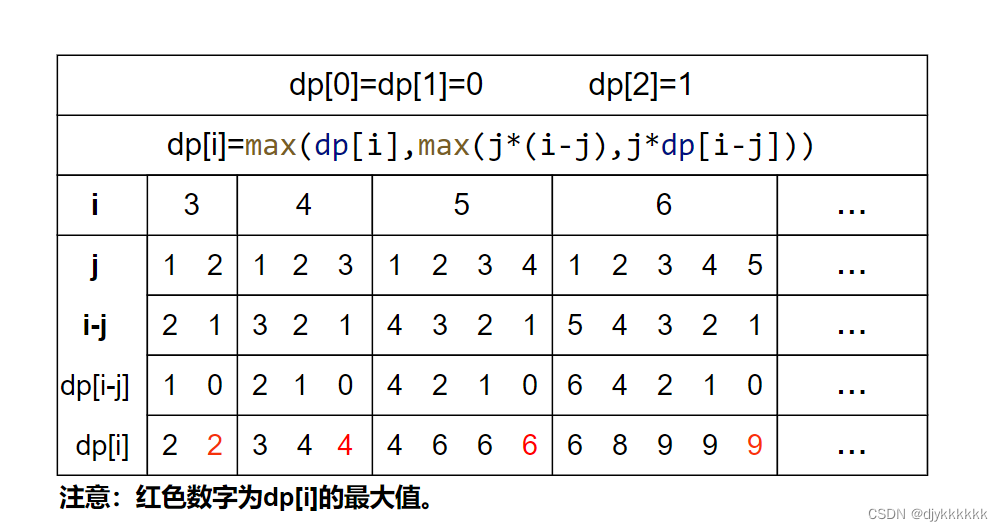
- 1.dp存储的是第i个数,拆分之后最大乘积
- 2.dp[i]=max(dp[i],max(j*(i-j),j*dp[i-j]));
- 3.初始化:dp[0]=dp[1]=0,dp[2]=1;
- 4.遍历顺序:外层循环 3-n,内层循环 1-i
2.涉及两次取max:
- dp[i] 表示拆开的最大乘积,因为涉及多次计算
- j*(i-j) 表示拆成两个数
- j*dp[i-j] 表示拆成两个以上的数(dp[i-j] 就是剩下没拆的数,拆开的最大乘积)
class Solution {
public:int integerBreak(int n) {vector<int>dp(n+1,0);dp[2]=1;for(int i=3;i<=n;i++){for(int j=1;j<i;j++){dp[i]=max(dp[i],max(j*(i-j),j*dp[i-j]));cout<<i<<" "<<dp[i]<<endl;}}return dp[n];}
};
96.不同的二叉搜索树
分析:1-n有几种二叉搜索树
-
1.以1-n每个数为根节点
-
2.判断根节点左边和右边各有几个节点,只有结点数相同,组合的二叉搜索树种数就是一样的。
思路:
- 1.dp存储n个节点有多少种二叉搜索树
- 2.dp[i]=dp[i-1]*dp[n-i];
- 3.初始化:dp[0]=dp[1]=1,dp[2]=2;
- 4.遍历顺序:3-n
416.分割等和子集
分析:
- 数组要求分成两个等和子集,所以一定要有子集和为总和的一半
- 转换为:在集合中找数字,看能否组合成总和的一半值的子集
- 转换为:在总和一半容量的背包里,寻找子集刚好装满
思路一:
1.dp存储:容量为 j 时,装入物品的最大值
2.dp [ j ] =max ( dp [ j ] ,dp [ j - nums [i] ] + nums [ i ] )
3.初始化:所有值初始化为0
4.遍历顺序:外层遍历数字(顺序,物品),内层遍历数字(倒序,背包容量)
class Solution {
public:bool canPartition(vector<int>& nums) {int total=0;for(auto it:nums) total+=it;//求出总和if(total%2!=0) return false;//过滤不可拆成两半的情况int target=total/2;//背包容量vector<int>dp(10001,0);for(int i=0;i<nums.size();i++){//遍历物品for(int j=target;j>=nums[i];j--){//背包容量递减,最少能装入一个物品dp[j]=max(dp[j],dp[j-nums[i]]+nums[i]);//dp[j] 是不装当前物品//dp[j-nums[i]]+nums[i] 是装当前物品}}if(dp[target]==target) return true;//背包容量为target,装了target重的物品return false;}
};


![[Android AIDL] --- AIDL工程搭建](https://img-blog.csdnimg.cn/d82923ad99334993ab634ef916cc5ad1.png)