可分离滤波器核
空间滤波器核是一个二维矩阵,若它能够表示为两个一维矩阵的乘积时,则表示该滤波器核是可分离的。
例如,一个3x3的核,
w = [ 1 1 1 1 1 1 1 1 1 ] w=\begin{bmatrix} 1 & 1 & 1\\ 1 & 1& 1\\ 1 & 1& 1\\ \end{bmatrix} w= 111111111
它可以表示为两个一维矩阵的乘积
c = [ 1 1 1 ] c=\begin{bmatrix} 1 & 1 & 1\\ \end{bmatrix} c=[111]
r = [ 1 1 1 ] r=\begin{bmatrix} 1 & 1 & 1\\ \end{bmatrix} r=[111]
即
w = c r T w=cr^T w=crT
性质
可分离核的重要性是卷积结合律性质导致的计算优势,如果有一个核 w w w,它可以分为两个简单的核并满足 w = w 1 ∗ w 2 w=w_1*w_2 w=w1∗w2,则其满足
w ∗ f = ( w 1 ∗ w 2 ) ∗ f = ( w 2 ∗ w 1 ) ∗ f = w 2 ∗ ( w 1 ∗ f ) = ( w 1 ∗ f ) ∗ w 2 w*f=(w_1*w_2)*f=(w_2*w_1)*f=w_2*(w_1*f)=(w_1*f)*w_2 w∗f=(w1∗w2)∗f=(w2∗w1)∗f=w2∗(w1∗f)=(w1∗f)∗w2
对于一个大小为 M ∗ N M*N M∗N的图像与大小为 m ∗ n m*n m∗n的核实现卷积,需要 M N m n MNmn MNmn次加法和乘法,如果核是可分离的,则需要 M N ( m + n ) MN(m+n) MN(m+n)次,可加速计算。
必要条件
要确定一个核是否可分离,只需要确定其秩是否为1。 因此确定某个矩阵的秩为1后,能够计算其两个分离的一维核,步骤如下
- 在核中找到任意一个非零元素,并将其表示为E;
- 找他该元素所在的行和列,表示为 c , r c,r c,r;
- 可以得出两个一维核为 c c c和 r / E r/E r/E;
示例
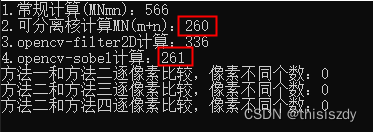
以x方向上的Sobel滤波核进行性能测试,比较 M N m n MNmn MNmn以及 M N ( m + n ) MN(m+n) MN(m+n)的处理时间,并与自带opencv 的cv::filter2D与cv::Sobel算子进行比较滤波效果。
int main()
{//x方向的Sobel核Mat kernel = (Mat_<char>(3, 3) <<-1, 0, 1,-2, 0, 2,-1, 0, 1);const char* imageName = ".....";Mat src = imread(imageName, IMREAD_GRAYSCALE);Mat srcBorder;copyMakeBorder(src, srcBorder, kernel.cols / 2, kernel.cols / 2, kernel.rows / 2, kernel.rows / 2, cv::BORDER_CONSTANT);//填充边缘clock_t start, end;//1.MNmnMat dst(src.rows, src.cols, CV_8UC1);start = clock();int sum = 0;for (int i = 1;i <= dst.rows;i++){for (int j = 1;j <= dst.cols;j++){sum = 0;for (int m = 0;m < kernel.rows;m++){for (int n = 0;n < kernel.cols;n++){sum += (int)(srcBorder.ptr<uchar>(i + m - 1)[j + n - 1] * kernel.ptr<char>(m)[n]);}}dst.ptr<uchar>(i - 1)[j - 1] = (uchar)(sum < 0 ? 0 : (sum > 255 ? 255 : sum));}}end = clock();std::cout << "1.常规计算(MNmn):" << end - start << std::endl;//2.可分离滤波计算Mat _src2(src.rows + kernel.rows / 2 + 1, src.cols + kernel.cols / 2 + 1, CV_32SC1);_src2 = Scalar::all(0);Mat dst2(src.rows, src.cols, CV_8UC1);start = clock();//分离卷积核char kernelRow[3] = { 1,0,-1 };char kernelCol[3] = { -1,-2,-1 };for (int i = 1;i <= dst2.rows;i++){for (int j = 1;j <= dst2.cols;j++){sum = 0;for (int m = 0;m < 3;m++){sum += (int)(srcBorder.ptr<uchar>(i)[j + m - 1] * kernelRow[m]);}_src2.ptr<short>(i)[j] = sum;}}for (int i = 1;i <= dst2.rows;i++){for (int j = 1;j <= dst2.cols;j++){sum = 0;for (int n = 0;n < 3;n++){sum += (int)(_src2.ptr<short>(i + n - 1)[j] * kernelCol[n]);}dst2.ptr<uchar>(i - 1)[j - 1] = (uchar)(sum < 0 ? 0 : (sum > 255 ? 255 : sum)); //防止溢出。opencv中使用内联函数saturate_cast<T>()}}end = clock();std::cout << "2.可分离核计算MN(m+n):" << end - start << std::endl;//3.opencv-filter2D计算Mat dst3;start = clock();cv::filter2D(src, dst3, -1, kernel, Point(-1, -1), 0.0, BORDER_CONSTANT);end = clock();std::cout << "3.opencv-filter2D计算:" << end - start << std::endl;//4.opencv-sobel计算Mat dst4;start = clock();cv::Sobel(src, dst4, -1, 1, 0, 3, 1.0, 0.0, BORDER_CONSTANT);end = clock();std::cout << "4.opencv-sobel计算:" << end - start << std::endl;// 效果比较Mat findzero1 = dst2 != dst4; //方法一和方法二比较效果Mat findzero2 = dst2 != dst4; //方法二和方法三比较效果Mat findzero3 = dst2 != dst4; //方法二和方法四比较效果vector<cv::Point> veczero1;vector<cv::Point> veczero2;vector<cv::Point> veczero3;cv::findNonZero(findzero1, veczero1);cv::findNonZero(findzero2, veczero2);cv::findNonZero(findzero3, veczero3);int num1 = veczero1.size();int num2 = veczero2.size();int num3 = veczero3.size();std::cout << "方法一和方法二逐像素比较,像素不同个数:" << num1 << std::endl;std::cout << "方法二和方法三逐像素比较,像素不同个数:" << num2 << std::endl;std::cout << "方法二和方法四逐像素比较,像素不同个数:" << num3 << std::endl;system("pause");return 0;
}
计算结果显示,可分离核计算比常规计算快一倍左右,与OpenCV的sobel算子处理时间相当。


![java八股文面试[JVM]——JVM性能优化](https://img-blog.csdnimg.cn/img_convert/944a51e6faf749f92a3778a203c66a1b.png)


