1 原理
如下图所示, 四边形ABCD, P在四边形内部,Q在四边形外部。
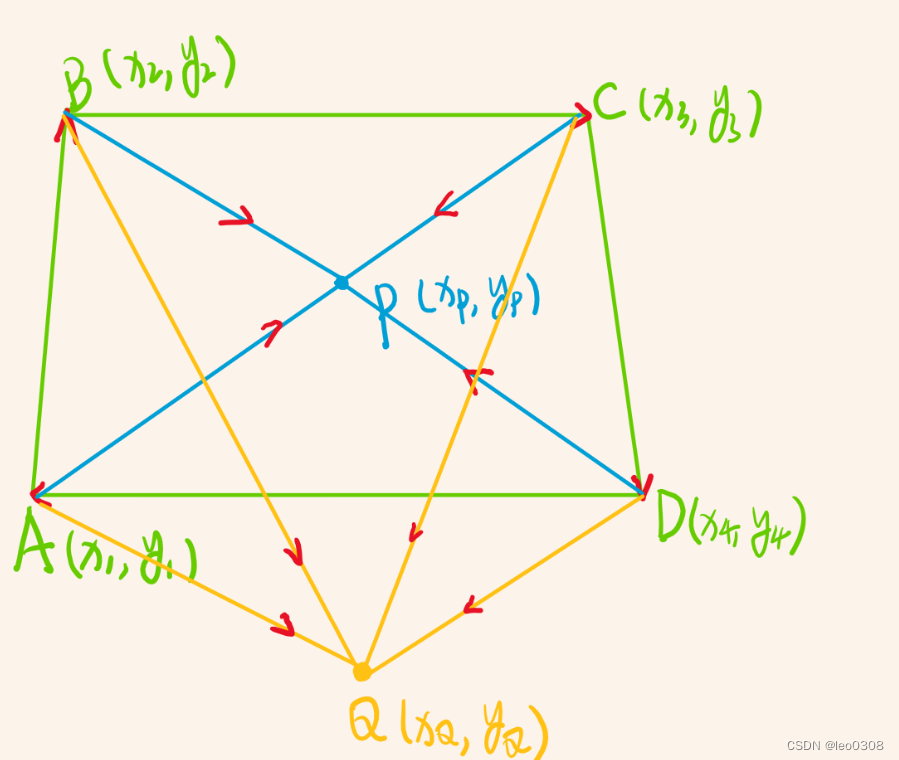
通过观察可以发现, 当点在四边形内部时, 如果按顺时针方向的话, 点P在四条边AB, BC, CD, DA的右侧。 当然如果按逆时针的话, 点P在四条边的左侧。
点Q在AB,BC和CD的右侧, 但在DA的左侧。因此可以通过方向的一致性判断点是否位于多边形内部。
判断方向可以通过向量的叉积运算。
A B ⃗ \vec{AB} ABx A P ⃗ \vec{AP} AP, B C ⃗ \vec{BC} BCx B P ⃗ \vec{BP} BP, C D ⃗ \vec{CD} CDx C P ⃗ \vec{CP} CP, D A ⃗ \vec{DA} DAx D P ⃗ \vec{DP} DP如果同方向, 那么P点就在多边形内部,否则就不在内部。
向量叉乘的结果是一个向量, 二维向量叉乘时, 结果向量的方向垂直于这2个向量。
其实不必要求是顺时针方向, 逆时针也可以, 逆时针顺序时4个向量叉积就都是小于0了。 因此只要4个向量叉乘是同时为正, 或同时为负就行。
2 向量叉积
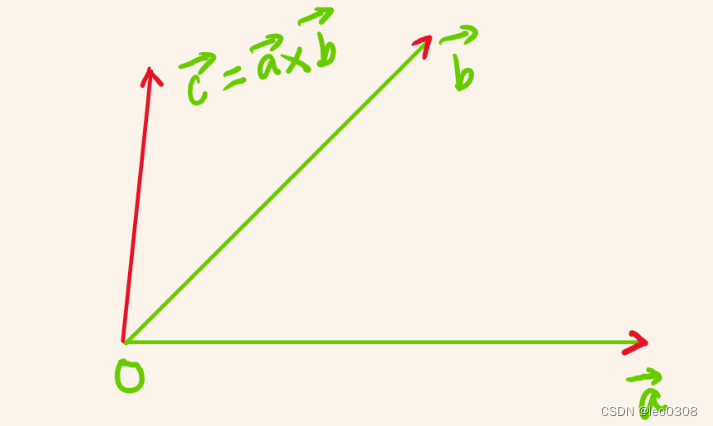
假设有2个向量 a ⃗ = ( x 1 , y 1 ) \vec{a}=(x_1, y_1) a=(x1,y1), b ⃗ = ( x 2 , y 2 ) \vec{b}=(x_2,y_2) b=(x2,y2), a ⃗ \vec{a} a与 b ⃗ \vec{b} b的叉积是一个向量,方向垂直于 a ⃗ \vec{a} a与 b ⃗ \vec{b} b所在的平面, 遵循右手法则。
a ⃗ \vec{a} ax b ⃗ \vec{b} b= 0 i ⃗ + 0 j ⃗ + ( x 1 y 2 − x 2 y 1 ) k ⃗ 0\vec{i}+0\vec{j}+(x_1y_2-x_2y_1)\vec{k} 0i+0j+(x1y2−x2y1)k
3 一些思考
其实最开始观察时, 发现了另外一个规律仿佛也奏效, 那就是 A B ⃗ \vec{AB} AB与 A P ⃗ \vec{AP} AP, B C ⃗ \vec{BC} BC与 B P ⃗ \vec{BP} BP, C D ⃗ \vec{CD} CD与 C P ⃗ \vec{CP} CP, D A ⃗ \vec{DA} DA与 D P ⃗ \vec{DP} DP夹角都是小于90度的, 对Q点对应的向量夹角, 有些是小于90度, 有些是大于90度的, 那么通过向量的内积也可以判断。其实这个规律不是普世的, 可以举出反例, P点在多边形内部时, 也会出现同时有大于90度和小于90度的角。
如下图所示:
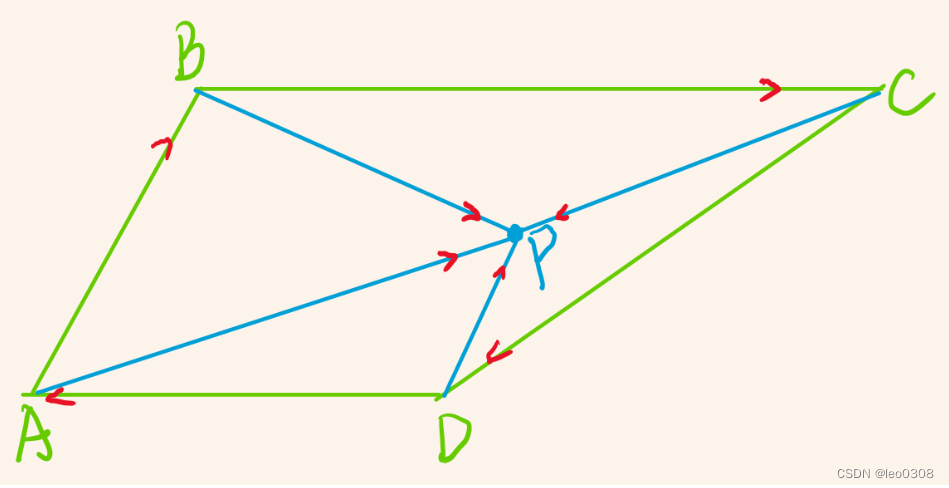
D A ⃗ \vec{DA} DA与 D P ⃗ \vec{DP} DP夹角是大于90度的, 而其他向量夹角是小于90度的。
上面的判断方法(指的是根据向量外积), 只适用于任意的凸多边形, 对非凸多边形是不适用的。
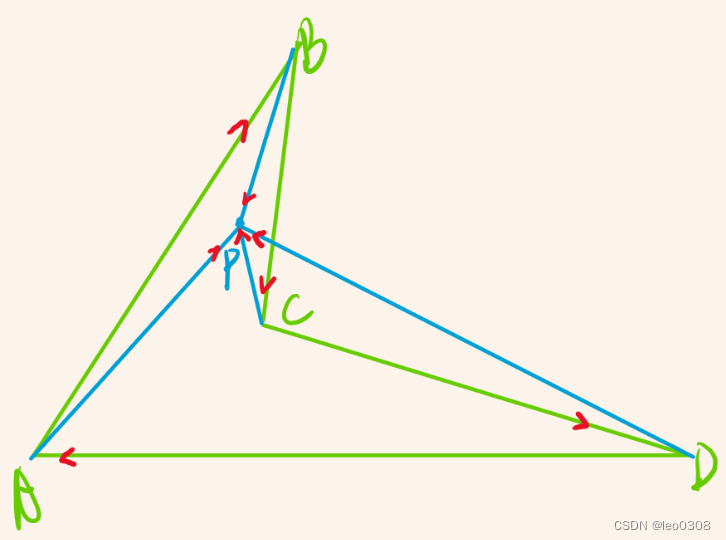
如上图所示, 对于非凸多边形, C D ⃗ \vec{CD} CDx C P ⃗ \vec{CP} CP的方向与其他向量就不同。
4 代码实现
import numpy as npdef isPointInArea(point, area):""":param point: [x,y]:param area: [[x1,y1],[x2,y2],[x3,y3],...]:return: if point is in area, return True, else False"""area_point_num = len(area)if area_point_num < 3:raise ValueError(f"the point number of the area must >=3, but get {area_point_num}")area.append(area[0])area = np.asarray(area)orientations = []xp, yp = point[0], point[1]for index in range(area_point_num):a = area[index + 1] - area[index]b = (xp - area[index, 0], yp - area[index, 1])ori = a[0] * b[1] - b[0] * a[1]orientations.append(ori)orientations = np.asarray(orientations)flags = orientations > 0if flags.sum() == area_point_num or flags.sum() == 0:return Trueelse:return Falseif __name__ == "__main__":point = [0.5, 1.5]area = [[0, 0], [0, 2], [2, 2], [2, 0]]flag = isPointInArea(point, area)print(flag)

![[国产MCU]-W801开发实例-MQTT客户端通信](https://img-blog.csdnimg.cn/f6159728c6d74fc8bb888e440eddc698.png#pic_center)