栈和队列

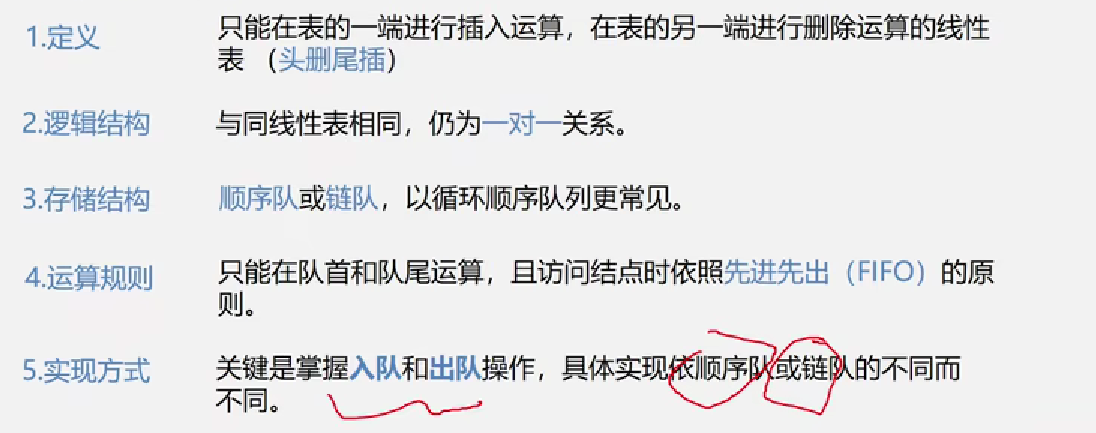
3.1 栈和队列的定义和特点

栈 (stack) 是限定仅在表尾进行插入或删除操作的线性表。 因此， 对栈来说， 表尾端有其 特殊含义， 称为栈顶 (top), 相应地， 表头端称为栈底 (bottom/base)。 不含元素的空表称为空栈。

栈是按后进先出的原则进行的， 如 图(a) 所示。 因此， 栈又称为后进先出 (Last In First Out, LIFO) 的线性表

插入元素叫入栈（PUSH），删除元素叫弹栈（POP）

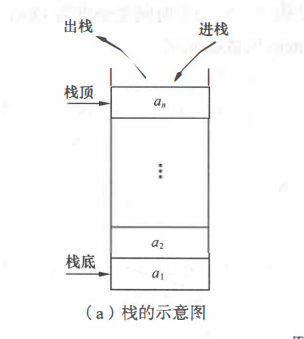
栈与一般线性表的区别：

和栈相反，队列(queue)是一种**先进先出(First In First Out, FIFO)**的线性表。它只允许在表 的一端进行插入，而在另一端删除元素。

在队列中，允许插入的一端称为队尾(rear), 允许 删除的一端则称为队头(front)。

3.2 案例引用

**【案例3.1】**进制转换

将十进制整数 N 向其他进制数d（二、八、十六）的转换

转换法则： N除以d倒取余

例如：将十进制数159转换成八进制数

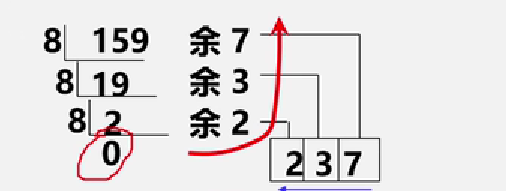
利用栈的先进后出，将每次计算结果入栈，最终取出来的就是结果

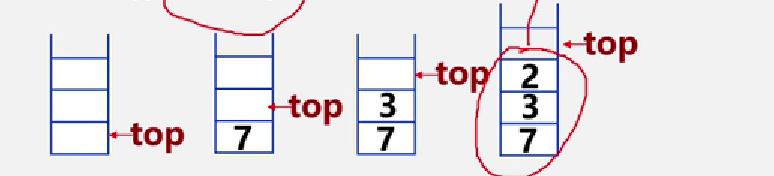
**【案例3.2】**括号匹配的校验

假设表达式中允许包含两种括号: 圆括号和方括号

遇见左括号就入栈，遇见右括号就与栈顶元素相比较，符合就弹栈，不符合就是不匹配。

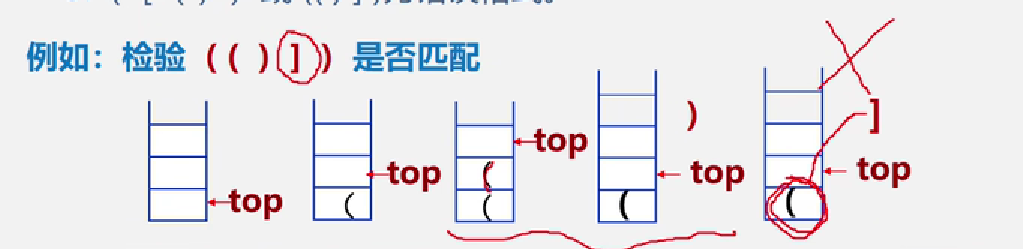
**【案例3.3】**表达式求值

这里介绍的算法是由运算符优先级确定运算顺序的对表达式求值算法—— 算符优先算法

表达式组成：

操作数(Qperand): 常数、变量

运算符(operator): 算术运算符、关系运算符和逻辑运算符

界限符(delimiter) :左右括弧和表达式结束符。

任何一个算术表达式都由操作数(常数、变量)、算术运算符(+、-、/)和界限符 (括号、表达式结束符“#'、虚设的表达式起始符# )组成。后两者统称为算符。

例如：# 3* （7-1）#

3.3 栈的顺序表示和实现

栈的抽象数据类型的定义

顺序栈的表示和实现

由于栈本身就是线性表，于是栈也有顺序存储和链式存储俩种实现方式。顺序存储——顺序栈 | 链式存储——链栈

存储方式: 同一般线性表的顺序存储结构完全相同

利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素。栈底一般在低地址端。

使用俩个指针base、top：base指向栈底元素，top指向栈顶元素。但是为了操作方便，一般 top 指向栈顶的下一个存储地址。另外使用一个 stacksize 表示栈的最大容量。

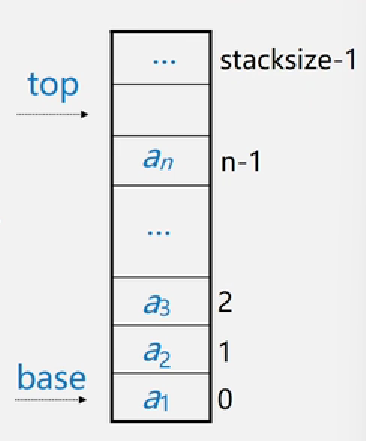
空栈时，base 和 top 同时指向栈底，没有元素可以弹栈，只能入栈

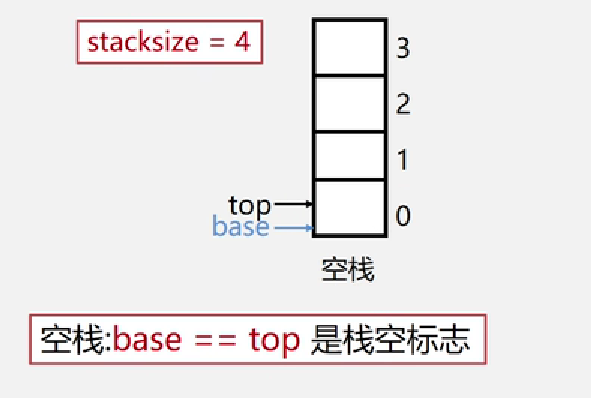
满栈时，top 与 base 的差值等于stacksize，不允许在入栈，只能弹栈

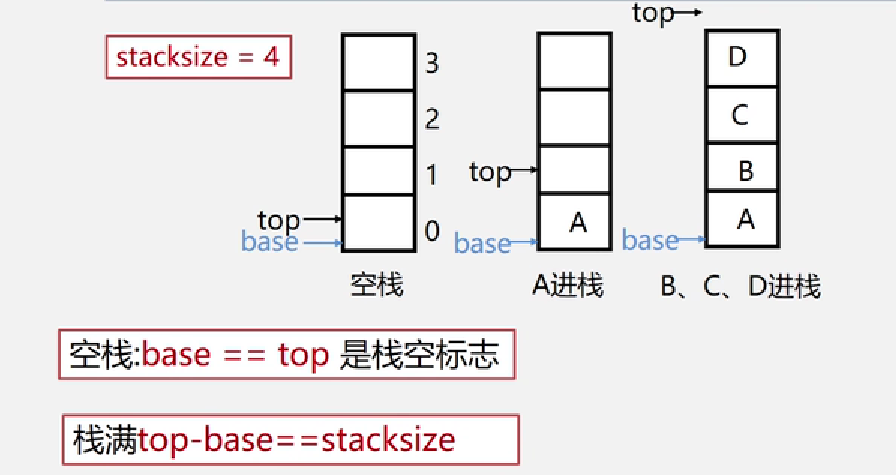
使用数组作为顺序栈存储方式特点：

简单、方便，但是容易产生溢出【数组大小固定】

上溢(overflow)：栈已经满，又要压入元素

下溢(underflow)：栈已经空，还要弹出元素

---

代码实现栈的初始化：

public class Stack {// 栈的最大容量public int stackSize;// top指针，指向栈顶public int top;// base指针，指向栈底public int base;// 使用数组模拟栈public Object[] stack;// 初始化栈public Stack(int stackSize) {this.stackSize = stackSize;stack = new Object[stackSize];top = 0;base = 0;}/*** 是否空栈* */public boolean isEmpty(){return top == base;}/*** 满栈* */public boolean isFull(){return  (top - base) == stackSize;}/*** 栈的长度* */public int getLength(){return  top - base;}/*** 清空栈* */public void clear(){this.top = this.base;}}

顺序栈的入栈

• 判断顺序栈是否已经满了，若满了抛出异常
• 将元素压入栈
• top指针+1

    /*** 入栈* */public void push(Object e) {if (isFull()) {throw new RuntimeException("栈满");}stack[top++] = e;}

顺序栈的出栈

• 判断是否栈空，若空抛出异常
• top指针-1
• 弹出元素

    /*** 出栈* */public Object pop(){if (isEmpty()) {throw new RuntimeException("栈空");}return stack[--top];}

3.4 栈的链式表示和实现

链栈是运算受限的单链表，只能在链表头部进行操作

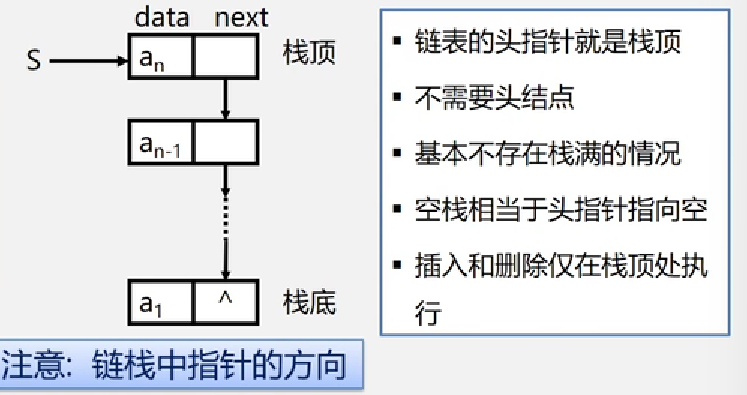
通过上面的图片，可以看出链表的方向是和单链表相反的，从 an ~ a1，这样的目的主要是为了操作方便，栈的弹栈、入栈都是从表头开始的，这样不会影响后续结点。

链栈的初始化：

public class ChainedStack {// 头指针Node s;public ChainedStack() {this.s = null;}
}

入栈操作：

入栈结点p，将p结点的next域指向s，s重新指向栈顶

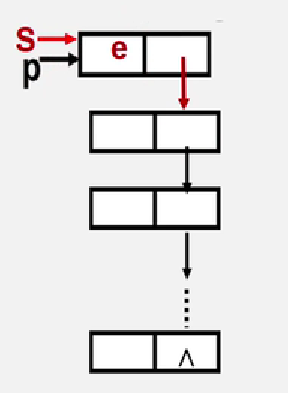
    /*** 入栈* */public void push(Node p) {// 将新结点指向栈顶元素p.next = s;// 更改指针s = p}

弹栈操作：

将弹出的结点使用一个指针p保存，将s指向p.next

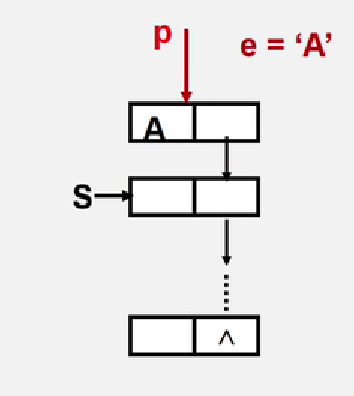
/*** 弹栈* */public Object pop(){if (s == null) {throw new RuntimeException("空栈");}Node res = s;s = res.next;return res.data;}

取栈顶元素

    /*** 取栈顶元素* */public Object getTop(){if (s == null) {throw new RuntimeException("空栈");}return s.data;}

3.5 队列的顺序表示和实现

与栈不同的是，无论是弹栈、压栈始终是移动一个栈顶指针，而队列中，出队移动front头指针，入队移动rear尾指针。

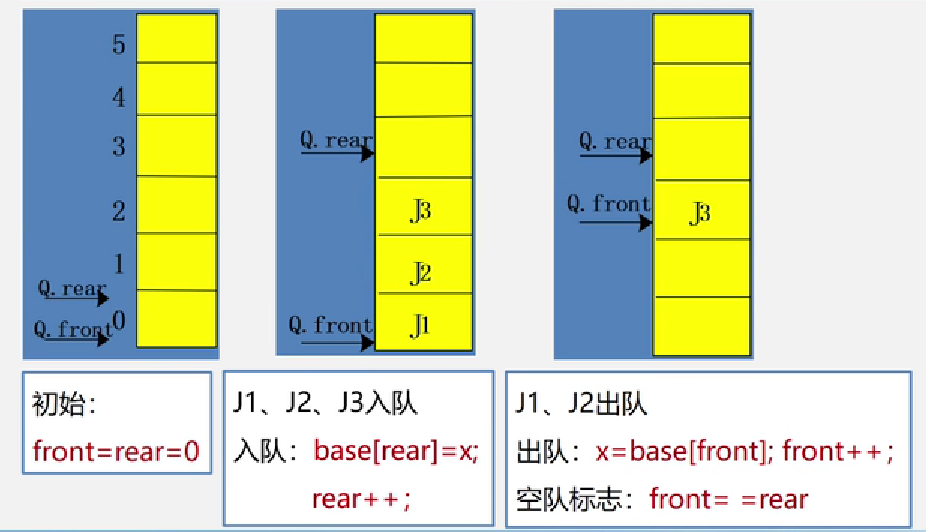
代码实现：

public class Queue {int maxSize; // 队列的最大容量Object[] queue;int front; // 头指针int rear; // 尾指针public Queue(int maxSize) {this.maxSize = maxSize;queue = new Object[maxSize];front = 0 ;rear = 0;}// 是否为空队列public boolean isEmpty(){return front == rear;}// 是否为满队列public boolean isFull(){return rear == maxSize-1;}// 获取队列元素的个数public int getLength(){return front - rear;}// 入队public void add(Object e){if (isFull()) {throw new RuntimeException("满队");}queue[rear++] = e;}// 出队public Object out(){if (isEmpty()){throw new RuntimeException("空队");}Object o = queue[front];// 将出队的元素存放位置置空queue[front++] = null;return o;}}

问题

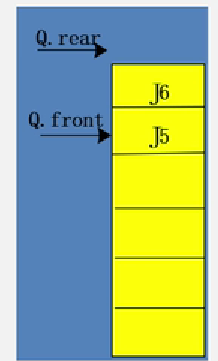
假设当 rear 已经等于 maxSize【黄色部分为队列长度】之后，还能入队吗？

答案是不能的，数组下标是从0开始的，rear= maxSize时，在入队就已经越界了。

其实我们发现下标从 0~front 之间是没有存储元素的，长度虽然为 6，但实际上存储了俩个元素，并没有真正的存满，这种情况就称为 假溢出

相对应的有真溢出，就是front = 0，rear = maxsize， 之间已经存满了元素，此时在入队就已经没有位置了。这种情况就无需处理了，而假溢出才是我们真正要解决的。

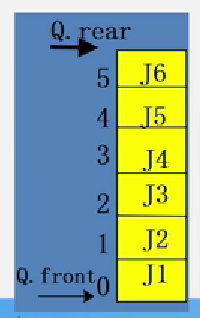
解决 假溢出 情况:

使用循环队列的方式解决假溢出情况， 当 rear = maxSize 时，让 rear 重新从 指向 0 的位置，当入队时，插入在 0 的位置上

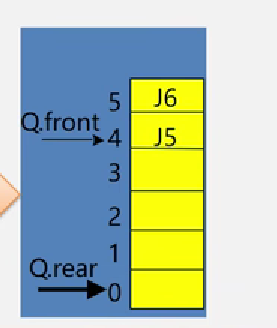
那么怎么让 rear 重新变为0 呢？ 可以利用模运算（取余）

当 rear =1，maxSize=6时，1% 6 = 1， 此时rear指向 1

当 rear =2，maxSize=6时，2% 6 = 2， 此时rear指向 2

…

当 rear =6，maxSize=6时，6% 6 = 0， 此时rear指向 0

插入元素e： queue[rear] = e; (rear+1) % maxSize
删除元素： e =  queue[front]; (front+1) % maxSize

循环队列如何判断空队列和满队列呢？

在循环队列中，可以发现无论是空队还是满队，都是 front == rear

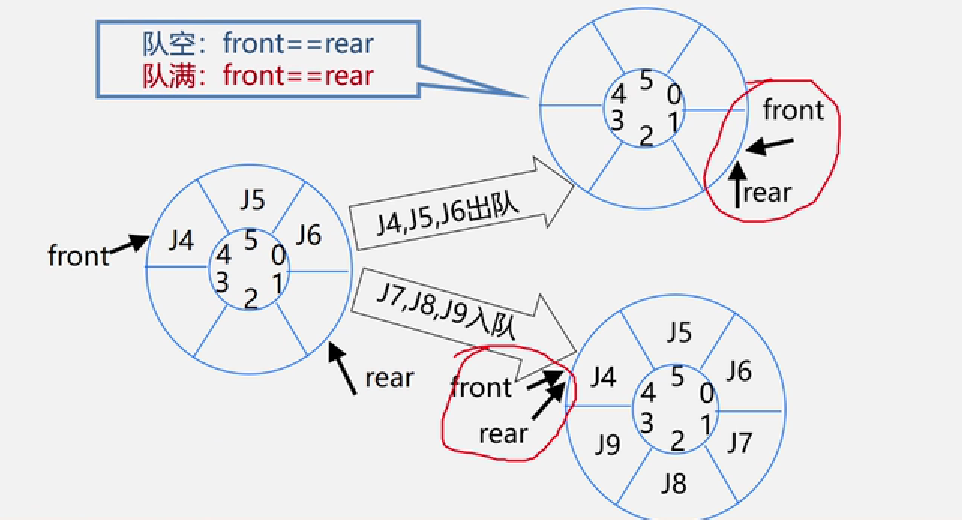
解决方案：

1.另外设一个标志以区别队空

2.另设一个变量录元素个数

3.少用一个元素空间

我用的是第二种方式，易于理解。

代码实现：

public class CircularQueues {Object[] queue;int front;int rear;int maxSize;int count; // 用来记录元素的个数// 初始化队列public CircularQueues(int maxSize) {this.maxSize = maxSize;this.front = 0;this.rear = 0;this.queue = new Object[maxSize];this.count = 0;}/*** 判断是否为空* */public boolean isEmpty() {return count == 0;}/*** 判断是否为满* */public boolean isFull() {return count == maxSize;}/*** 入队* */public void add(Object e) {if (isFull()) {throw new RuntimeException("满队");}// 入队操作queue[rear] = e;rear = (rear + 1) % maxSize;// 记录数+1count++;}/*** 出队* */public Object out() {if (isEmpty()) {throw new RuntimeException("空队");}Object e = queue[front];front = (front + 1) % maxSize;// 记录数-1count--;return e;}/*** 获取对头元素* */public Object getHeadEle() {if (isEmpty()) {throw new RuntimeException("空队");}return queue[front];}
}

3.6 队列的链式表示和实现

顺序队列采用数组实现，大小固定，若无法估计队列的长度，直接使用链式队列。

头指针的指向头结点，尾指针指向尾结点。

链队列指针变化情况：

初始情况下，头指针、尾指针都指向头结点

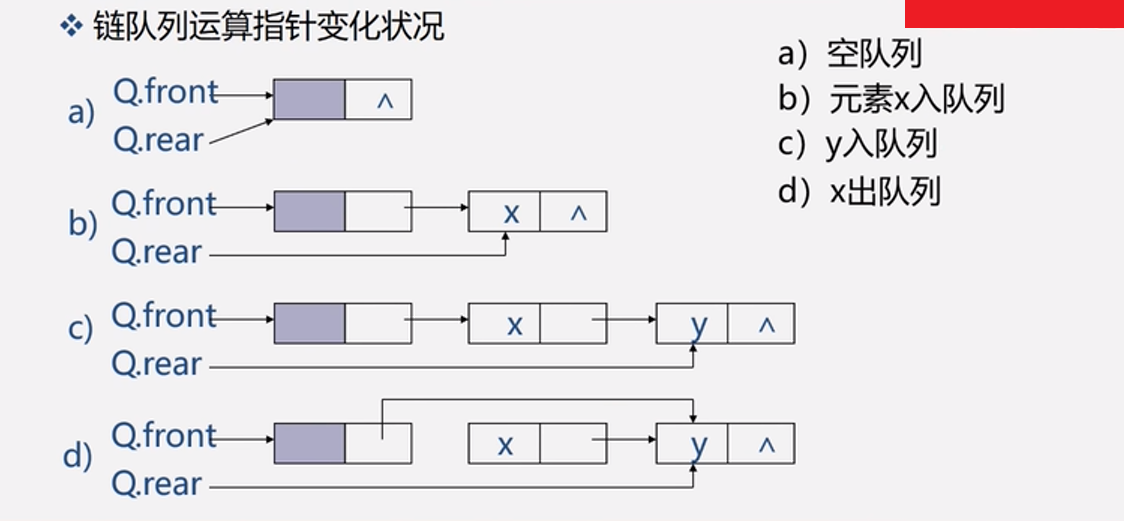
链队列的初始化：

public class ChainedQueues {// 头指针Node front;// 尾指针Node rear;// 头指针Node dummyHead;public ChainedQueues() {// 初始化，头结点的数据随意，可以不设置this.dummyHead = new Node(-1);this.front = dummyHead;this.rear = dummyHead;}
}

入队操作：

头删尾插，将rear指针的next域指向新结点，并将 rear指针后移即可。

    /*** 入队* */public void add(Node e) {rear.next = e;rear = e;}

出队操作：

出队操作时将首元结点删除掉并返回，很简单，头指针的next域就是要出队的元素。

    public Object out() {if (rear == front) {throw new RuntimeException("队空");}Node res = front.next;front.next = res.next;return res.data;}

但是这样写会有一些问题，如果出队的正好是队尾元素，此时 front.next = null， 但是 rear 指针仍然在指向 res，因此判断非空时，会返回 false

因此当出队的是队尾元素还需要将 rear 指针重新指向头结点。

    /*** 出队* 如果出队的是最后一个结点，还要修改尾指针* */public Object out() {if (isEmpty()) {throw new RuntimeException("队空");}Node res = front.next;front.next = res.next;if (res == rear) {// 最后一个结点rear = dummyHead;}return res.data;}