激活函数
将输入信号的总和转换为输出信号,一般称为激活函数(activation function)。激活函数作用在于决定如何来激活输入信号的总和。
对激活函数,一般要求:
- 非线性:为提高模型的学习能力,如果是线性,那么再多层都相当于只有两层效果。
- 可微性:有时可以弱化,在一些点存在偏导即可。
- 单调性:保证模型简单。
激活函数在神经网络中的作用有很多,主要作用是给神经网络提供非线性建模能力。如果没有激活函数,那么再多层的神经网络也只能处理线性可分问题。
神经网络使用的激活函数:
(记住激活函数的表达式和对应的图形)
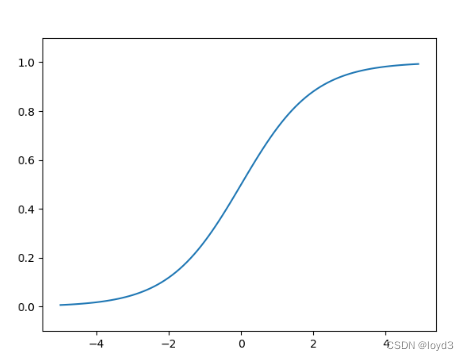
sigmoid函数
优点在于输出映射在(0,1)内,单调连续,适合用作输出层,求导容易;缺点是具有软饱和性,一旦输入数据落入饱和区,一阶导数变得接近0,就可能产生梯度消失问题。
公式
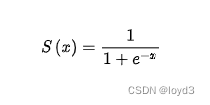
在python中实现sigmoid函数
def sigmoid(x):return 1 / (1+ np.exp(-x))
这里 np.exp(-x)对应exp(-x),要注意的是参数x为NumPy数组,结果也能正确计算,sigmoid的运算会在NumPy数组的各个元素间进行
函数图形
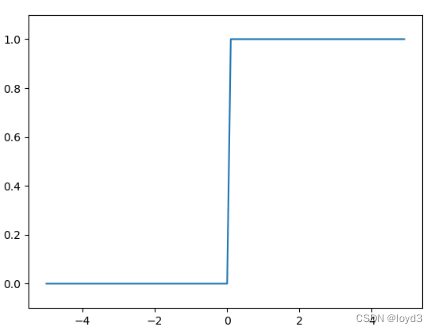
阶跃函数
阶跃函数的定义当输人超过0时,输出1否则输出0。
实现如下:
def step_function(x):return np.array(x > 0, dtype=int)
tip: 对NumPy数组进行不等号运算后,数组的各个元素都会进行不等号原酸生成一个布尔型数组。然后将数组y的元素类型从布尔型转换为int型
函数图形
sigmoid函数和阶跃函数的比较
- “平滑性”的不同:阶跃函数只能返回0或1,sigmoid函数可以返回0.71、0.80等实数
- 两个函数具有相同的形状,两者的结构均是“输入小时,输出接近0(为0),随着输人增大,输出向1靠近(变成1)。
- 两者均为非线性函数
要注意的是:神经网络的激活函数必须使用非线性函数。因为使用线性函数的话,加深神经网络的层数就没有意义了。也就是常说的断线性。
线性函数的问题在于,不管如何加深层数,总是存在与之等效的“无隐藏层的神经网络”。例如:这里我们考虑把线性函数h(z)=c作为激活函数,把y(z)=h(h(h(z)))的运算对应3层神经网络·。这个运算会进行y(z)=c x c x c x X的乘法运算,但是同样的处理可以由y(z)=az(注意a=c3)这一次乘法运算(即没有隐藏层的神经网络)来表示。换言之,用线性函数无法发挥叠加层的作用
ReLU函数
relu函数是目前最受欢迎的激活函数,在x<0时,硬饱和,x>0时,导数为1,所以在x>0时保持梯度不衰减,从而可以缓解梯度消失问题,能更快收敛,并提供神经网络的稀疏表达能力。但随着训练的进行,部分输入会落入硬饱和区,导致对应的权重无法更新,称为“神经元死亡”
ReLU函数在输人大于0时,直接输出该值;在输入小于等于0时,输出0
ReLU函数的实现如下:
def relu(x):return np,maximum(0,x)
函数图形

tanh
tanh激活函数同样具有软饱和性,输出以0为中心,收敛速度比tanh激活函数同样具有软饱和性,输出以0为中心,收敛速度比sigmoid快,但是也存在梯度消失问题
tanh函数公式如下:

在python的实现如下:
def tanh(x):return np.tanh(x)
图形如下:

在搭建神经网络时,如何选择激活函数?
如果搭建的神经网络层数不多,选择sigmoid、tanh、relu、softmax都可以;
如果搭建的网络层次比较多,那就需要小心,选择不当就可导致梯度消失问题。此时一般不宜选择sigmoid、tanh激活函数,因它们的导数都小于1,尤其是sigmoid的导数在[0,1/4]之间,多层叠加后,根据微积分链式法则,随着层数增多,导数或偏导将指数级变小。所以层数较多的激活函数需要考虑其导数不宜小于1,当然导数也不能大于1,大于1将导致梯度爆炸,导数为1最好,激活函数relu正好满足这个条件。所以,搭建比较深的神经网络时,一般使用relu激活函数,虽然一般神经网络也可使用。此外,激活函数softmax由于Σσi(Z)=1,常用于多分类神经网络输出层。
补充
饱和,软饱和,硬饱和的概念
- 饱和
当x趋近于正无穷,h(x)趋近于0,称之为右饱和。
当n趋近于负无穷,h(x)趋近于0,称之为左饱和。
当一个函数既满足左饱和又满足右饱和的时候就称之为饱和。 - 硬饱和
对于任意的x,如果存在常数c,当x>c时,恒有h(x)=0,则称其为右硬饱和。
如果对于任意的x,如果存在常数c,当x<c时,恒有h(x)=0,则称其为左硬饱和。
既满足左硬饱和又满足右硬饱和的我们称这种函数为硬饱和。 - 软饱和
对于任意的x,如果存在常数c,当x>c时,恒有h(x)趋近于0,则称其为右软饱和。
如果对于任意的x,如果存在常数c,当x<c时,恒有h(x) 趋近于0,则称其为左软饱和。
既满足左软饱和又满足右软饱和的我们称这种函数为软饱和。