前言：

适配器也称配接器（adapters）在STL组件的灵活组合运用功能上，扮演着轴承、转换器的角色。

《Design Patterns》对adapter的定义如下：将一个class的接口转换为另一个class的接口，使原本因接口不兼容而不能合作的classes可以一起运作。

---

目录

1 配接器概观与分类

​编辑 2 stack（栈）

2.1常用接口介绍 

2.2模拟实现

 3.queue（队列）

 3.1接口函数

3.2模拟实现

​编辑 4.小结

​编辑 5 deque（双端队列）

---

---

1 配接器概观与分类

stl所提供的各种配接器中，改变仿函数（functors）接口的，我们称作 function adapter，改变容器（containers）接口的，我们称为 container adapter，改变迭代器（iterators）接口的，我们称为 iterator adapter。 所以大致可以分为三类：

• 容器适配器 ：container adapters
• 迭代器适配器： iterator adapters
• 仿函数适配器 ：functor adapters

其中，容器适配器 可修改底层为指定容器，STL提供的两个容器 stack和queue 其实都只不过是一种适配器可以由 vector 构成的栈、由 list 构成的队列，最好由 deque修饰（文末会介绍）；迭代器适配器可以 实现其他容器的反向迭代器（后续介绍）；最后的仿函数适配器是所有适配器中数量最庞大的，适配灵活度远远高于前两者。，可以 无限制的创造出各种可能的表达式。 

 2 stack（栈）

既然 栈可由适配器构成。我们就从栈开始 ，栈 stack 是一种特殊的数据结构，主要特点为 先进后出 FILO，主要操作有：入栈、出栈、查看栈顶元素、判断栈空等；栈在原则上是不允许进行中部或头部操作的，这样会破坏栈结构的完整性，就不叫栈了

 

 

从库中我们可以发现，实现栈的模板参数有两个 不带缺省值的是元素类型，同时也是适配器所需的元素类型，第二个就是适配器由deque实现。代码实现如下：

#include <iostream>
#include <stack>
#include <vector>
#include <list>using namespace std;int main()
{stack<int> s;	//库里默认底层容器为 dequestack<int, vector<int>> sv;	//显示实例化底层容器为 vectorstack<char, list<char>> sl;	//显示实例化底层容器为 listcout << typeid(s).name() << endl;	//查看具体类型cout << typeid(sv).name() << endl;cout << typeid(sl).name() << endl;return 0;
}

 

alloc是空间适配器 是库里专用的 他会层层 typedef 这里我们不多介绍后续专门介绍。 

2.1常用接口介绍 

 库里的接口都比较简单，知道接口函数，调用即可。

#include <iostream>
#include <stack>using namespace std;int main()
{stack<int> s;	//构造一个栈对象cout << "Original:>" << endl;cout << "empty(): " << s.empty() << endl;cout << "size(): " << s.size() << endl;cout << endl << "Push:>" << endl;s.push(1);	//入栈3个元素s.push(2);s.push(3);cout << "empty(): " << s.empty() << endl;cout << "size(): " << s.size() << endl;cout << "top(): " << s.top() << endl;cout << endl << "Pop:>" << endl;s.pop();	//出栈两次s.pop();cout << "empty(): " << s.empty() << endl;cout << "size(): " << s.size() << endl;cout << "top(): " << s.top() << endl;return 0;
}

2.2模拟实现

我们选择使用vector作为适配器模拟实现 ，代码如下：

#pragma once
#include <vector>using namespace std;namespace cmx
{//这里选择模板参数2 底层容器 的缺省值为 vectortemplate<class T, class Container = vector<int>>class stack{public://需要提供一个带缺省参数的构造函数，因为默认构造函数不接受传参stack(const Container& con = Container()):_con(con){}//不需要显式的去写析构函数，默认生成的够用了//同理拷贝构造、赋值重载也不需要bool empty() const{return _con.empty();}size_t size() const{return _con.size();}//top 需要提供两种版本T& top(){return _con.back();}const T& top() const{return _con.back();}//选取的底层容器必须支持尾部操作void push(const T& val){_con.push_back(val);}void pop(){//空栈不能弹出，可在底层容器中检查出来_con.pop_back();}private:Container _con;	//成员变量为具体的底层容器};
}

从上述代码中，我们可以看到我们可以利用vector的pushback作为我push的接口，适配器的厉害之处就在于 只要底层容器有我需要的函数接口，那么我就可以为其适配出一个容器适配器，比如 vector 构成的栈、list 构成的栈、deque 构成的栈，甚至是 string 也能适配出一个栈，只要符合条件，都可以作为栈的底层容器，当然不同结构的效率不同，因此库中选用的是效率较高的 deque 作为默认底层容器。

 

 3.queue（队列）

 队列 queue 是另一种特殊的数据结构，遵循先进先出 FIFO，主要操作：入队、出队、判断队空、查看队头尾元素等

 

 

和栈一样，队列也有两个模板参数：

• 参数1：T 队列中的元素类型，同时也是底层容器中的元素类型
• 参数2：Container 实现队列时用到的底层容器，这里为缺省参数，缺省结构为 双端队列 deque

创建队列对象时，我们也可以指定其底层容器：

#include <iostream>
#include<queue>
#include <vector>
#include <list>using namespace std;int main()
{queue<int> qDeque;	//默认使用 dequequeue<double, vector<double>> qVector;	//指定使用 vectorqueue<char, list<char>> qList;	//指定使用 listcout << typeid(qDeque).name() << endl;	//查看具体类型cout << typeid(qVector).name() << endl;cout << typeid(qList).name() << endl;return 0;
}

 3.1接口函数

常见接口的使用 代码如下：

 

#include <iostream>
#include <queue>using namespace std;int main()
{queue<int> q;	//构建出一个队列对象cout << "Original:>" << endl;cout << "empty(): " << q.empty() << endl;cout << "size(): " << q.size() << endl;cout << endl << "Push:>" << endl;q.push(1);q.push(2);q.push(3);q.push(4);q.push(5);cout << "empty(): " << q.empty() << endl;cout << "size(): " << q.size() << endl;cout << "front(): " << q.front() << endl;cout << "back(): " << q.back() << endl;cout << endl << "Pop:>" << endl;q.pop();q.pop();q.pop();cout << "empty(): " << q.empty() << endl;cout << "size(): " << q.size() << endl;cout << "front(): " << q.front() << endl;cout << "back(): " << q.back() << endl;return 0;
}

3.2模拟实现

 库里常见的适配器是deque，我们选用list作为底层适配器模拟实现

#pragma once
#include <list>using namespace std;namespace Yohifo
{template<class T, class Container = list<T>>class queue{public:queue(const Container& c = Container()):_c(c){}//这里也不需要提供拷贝构造、赋值重载、析构函数bool empty() const{return _c.empty();}size_t size() const{return _c.size();}//选取的底层容器中，已经准备好了相关函数，如 front、backT& front(){return _c.front();}const T& front() const{return _c.front();}T& back(){return _c.back();}const T& back() const{return _c.back();}void push(const T& val){_c.push_back(val);	//队列只能尾插}void pop(){_c.pop_front();	//队列只能头删}private:Container _c;	//成员变量为指定的底层容器对象};
}

队列和栈在进行适配时，都是在调用已有的接口，若是特殊接口，比如 top、push、pop 等，进行相应转换即可

栈 top -> back 尾元素
栈、队列 push -> push_back 尾插
栈 pop -> pop_back 尾删
队列 pop -> pop_front 头删

 4.小结

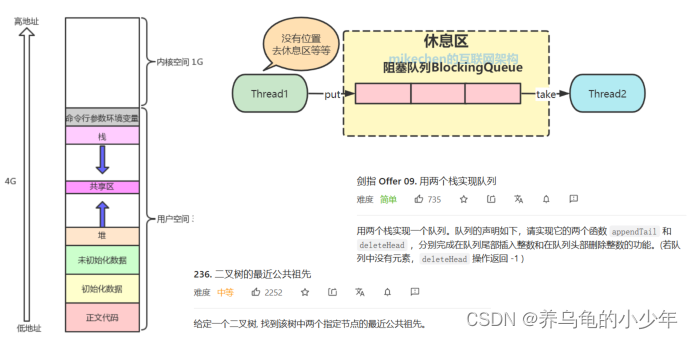
栈和队列在实际开发中作为一种辅助结构被经常使用，比如内存空间划分中的栈区，设计规则符合栈 FILO；操作系统中的各种队列，如阻塞队列，设计规则符合 队列 FIFO。除此以外，在很多 OJ 题中，都需要借助栈和队列进行解题 

 5 deque（双端队列）

 双端队列是官方指定的底层容器，其结构上的特殊设计决定了它只适合于头尾操作需求高的场景：双端队列 = vector + list，设计时就想汲取二者的优点（下标随机访问 + 极致的空间使用），但鱼和熊掌不可兼得，在复杂结构的加持之下，双端队列趋于中庸，无法做到 vector 和 list 那样极致，因此实际中也很少使用，比较适合当作适配器的底层容器

双端队列的数据结构：list + vector

利用 list 构造出一个 map 作为主控数组（通过链式结构链接），数组中元素为数组指针
利用 vector 构造出大小为 N 的小数组（缓冲区），这些小数组才是双端队列存储元素的地方
注意： 此处的 map 并非是容器 map，仅仅是名字相同。

 

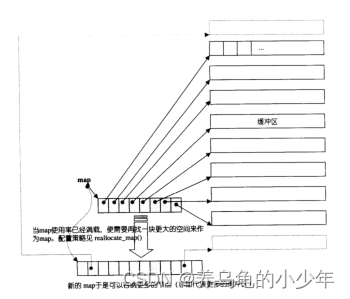
 deque 的扩容机制：只需要对中控数组 map 进行扩容，再将原 map 中的数组指针拷贝过来即可，效率比较高。

deque 中的随机访问：

1. (下标 - 前预留位) / 单个数组长度 获取对应小数组位置
2. (下标 - 前预留位) % 单个数组长度 获取其在小数组中的对应下标

 由此可见，单个数组大小（缓冲区大小）需要定长，否则访问时计算会比较麻烦，但长度定长后，会引发中间位置插入删除效率低的问题

对此 SGI 版的 STL 选择牺牲中间位置插入，提高下标随机访问速度，令小数组定长，这也是将它作为 栈和队列 默认底层容器的原因之一，因为 栈和队列 不需要对中间进行操作

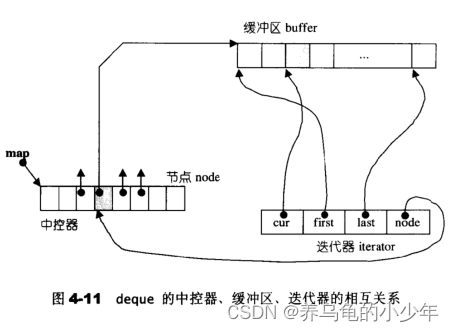
因为中控数组是链式结构，因此双端队列的迭代器设计极为复杂

cur 指向当前需要的数据位置
first 指向 buffer 数组起始位置
last 指向 buffer 数组终止位置
node 反向指向中控数组

 

这个迭代器还是一个随机迭代器，因此可以使用 std::sort

无论是 deque 还是 list，直接排序的效率都不如借助 vector 间接排序效率高
deque 的缺点

中间位置插入删除比较麻烦，可以令小数组长度不同解决问题，不过此时影响随机访问效率
结构设计复杂，且不如 vector 和 list 极致
致命缺陷：不适合遍历，迭代器需要频繁检测是否移动某段小空间的边界，效率很低
凑巧的是，栈和队列 可以完美避开所有缺陷，全面汲取其优点，因此 双端队列 为容器适配器的默认底层容器。