全排列[中等]-编程知识

全排列[中等]

优质博文：IT-BLOG-CN

一、题目

给定一个不含重复数字的数组nums，返回其所有可能的全排列。你可以按任意顺序返回答案。

示例 1：
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：
输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：
输入：nums = [1]
输出：[[1]]

提示：
1 <= nums.length <= 6
-10 <= nums[i] <= 10
nums 中的所有整数互不相同

二、代码

全排列的长度就是数据长度的阶层，排列和组合的区别：排列中[1,2]和[2,1]是不同的，但在组合中[1,2]和[2,1]是相同的。

我们已简单的[1,2,3]为一组，看下排列的搜索树：

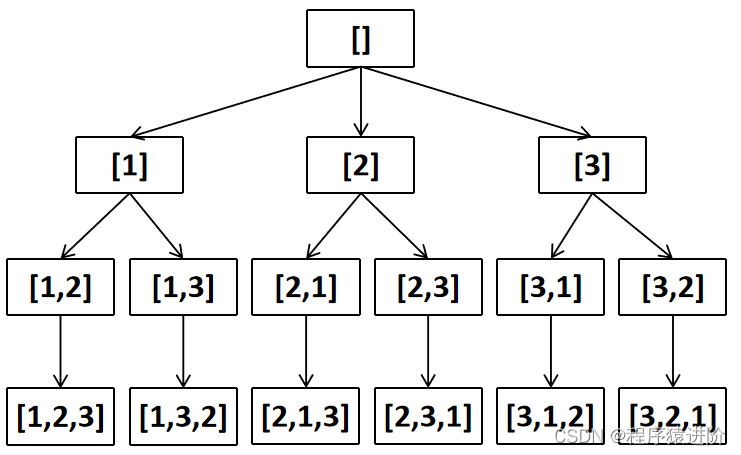
解题思路：
【1】使用数组path记录路径上的数（已选数字）
【2】集合s记录剩余未选的数

回溯三问：
【1】当前操作？从s中枚举path[i]要填入的数字x；
【2】子问题？构造排列 >= i 的部分，剩余未选数字集合为s；
【3】下一个子问题？构造排列 >= i + 1 部分，剩余未选数字结合为s-{x}；

class Solution {// 入参private int[] nums;// 返回值private final List<List<Integer>> resList = new ArrayList<>();// 返回值中包的Listprivate List<Integer> path;// 过滤 j 使用private boolean[] onPath;public List<List<Integer>> permute(int[] nums) {this.nums = nums;path = Arrays.asList(new Integer[nums.length]);onPath = new boolean[nums.length];dfs(0);return resList;}// 回溯方法private void dfs(int i) {// 回溯方法的退出条件if (i == nums.length) {// 这里需要copy path, 不能直接赋值，因为path一直变化resList.add(new ArrayList(path));System.out.println("resList : " + resList.toString());return;}// 每个i进来，组装一次结果for (int j = 0; j < nums.length; j++) {// 过滤j，原因在循环中有说明if (!onPath[j]) {// 当 i 递增时，j也在递增path.set(i, nums[j]);System.out.println(path.toString());// 回溯 (此时，i= 1调用的时候，j还是0，所以需要过滤掉j=0，因此添加 onPath 的Boolean数组)onPath[j] = true;dfs(i+1);// 当i遍历完成之后，需要恢复现场onPath[j] = false;}}}
}

看下输出的流程：

[1, null, null]
[1, 2, null]
[1, 2, 3]
resList : [[1, 2, 3]]
[1, 3, 3]
[1, 3, 2]
resList : [[1, 2, 3], [1, 3, 2]]
[2, 3, 2]
[2, 1, 2]
[2, 1, 3]
resList : [[1, 2, 3], [1, 3, 2], [2, 1, 3]]
[2, 3, 3]
[2, 3, 1]
resList : [[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1]]
[3, 3, 1]
[3, 1, 1]
[3, 1, 2]
resList : [[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2]]
[3, 2, 2]
[3, 2, 1]
resList : [[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]

附视频讲解

时间复杂度： O(n⋅n!)，其中n为nums的长度。搜索树中的节点个数低于3⋅n!。实际上，精确值为⌊e⋅n!⌋，其中e=2.718⋯为自然常数。每个非叶节点要花费O(n)的时间遍历onPath数组，每个叶结点也要花费O(n)的时间复制path数组，因此时间复杂度为O(n⋅n!)。
空间复杂度： O(n)返回值的空间不计入。