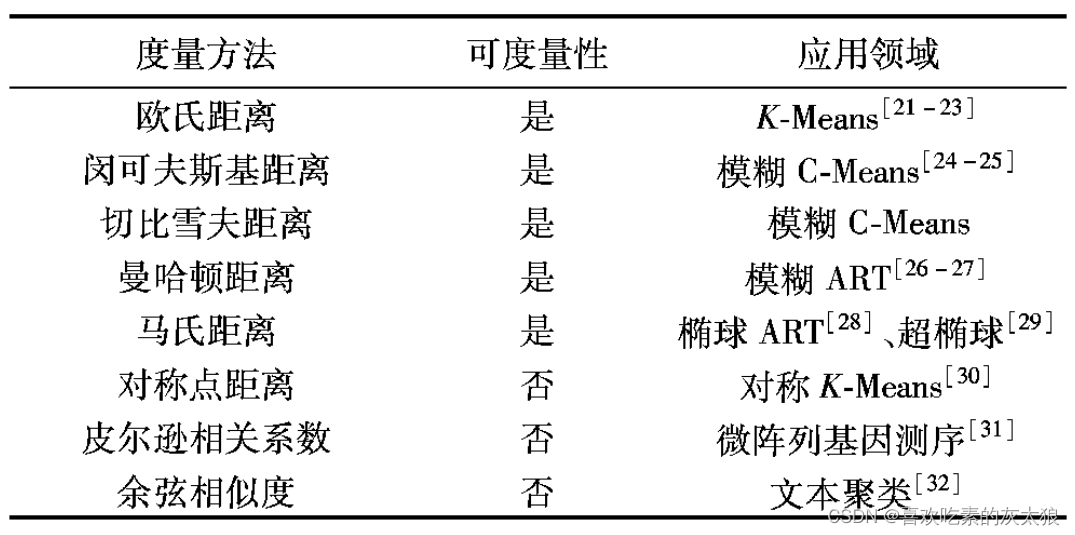
矩阵的相似性度量的常用方法
1,欧氏距离
欧式距离是最易于理解的一种距离计算方法,源自欧式空间中两点间的距离公式。
(1)二维平面上的点 a ( x 1 , y 1 ) a(x_1,y_1) a(x1,y1)和点 b ( x 2 , y 2 ) b(x_2,y_2) b(x2,y2)的欧式距离为
d = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2} d=(x1−x2)2+(y1−y2)2
(2)三维平面上的点 a ( x 1 , y 1 , z 1 ) a(x_1,y_1,z_1) a(x1,y1,z1)和点 b ( x 2 , y 2 , z − 2 ) b(x_2,y_2,z-2) b(x2,y2,z−2)的欧式距离为
d = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 + ( z 1 − z 2 ) 2 d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2} d=(x1−x2)2+(y1−y2)2+(z1−z2)2
不失一般性:
D ( X i , X j ) = ∑ l = 1 d ( x i l − x j l ) 2 D(X_i,X_j)=\sqrt{\sum_{l=1}^d(x_{il}-x_{jl})^2} D(Xi,Xj)=∑l=1d(xil−xjl)2
其中:D表示样本间的距离, X i , X j X_i,X_j Xi,Xj代表一个向量,或称为样本点或者样本;l是样本特征的维数, x i l , x j l x_{il},x_{jl} xil,xjl表示一个变量,或成为属性;d表示样本的总维数,即样本特征的总数量(下同)。
2,切比雪夫距离
在二维空间中,切比雪夫距离的典型应用是解决国际象棋中的国王从一个格子走到另一个格子最少需要几步的问题。这种距离在模糊C-Means方法中得到了有效应用。切比雪夫距离的公式可以表示为:
D ( X i , X j ) = m a x l ( ∣ x i l − x j l ∣ ) D(X_i,X_j)=max_l(|x_{il}-x_{jl}|) D(Xi,Xj)=maxl(∣xil−xjl∣)
此公式的另一种表示形式为:
D ( X i , X j ) = lim p → + ∞ ∑ l = 1 d ( x i l − x j l ) 2 p D(X_i,X_j)=\lim_{p\rightarrow+\infty}\sqrt[p]{\sum_{l=1}^d(x_{il}-x_{jl})^2} D(Xi,Xj)=limp→+∞p∑l=1d(xil−xjl)2
3,曼哈顿距离
在城市生活中,只能沿着街道从一个地方走到另一个地方,为此,人们将生活中熟悉的城市街区距离形象地称为曼哈顿距离。该距离的表示公式为:
D ( X i , X j ) = ∑ l = 1 d ( ∣ x i l − x j l ∣ ) D(X_i,X_j)=\sum_{l=1}^d(|x_{il}-x_{jl}|) D(Xi,Xj)=∑l=1d(∣xil−xjl∣)
曼哈顿距离在基于自适应谐振理论的同步聚类中有较好的应用;但是需要注意的是这种距离不再符合在特征空间中的转化和旋转的不变性。
4,闵可夫斯基距离
闵可夫斯基距离是一种p范数的形式,公式可以表示为:
D ( X i , X j ) = ∑ l = 1 d ( x i l − x j l ) 2 p D(X_i,X_j)=\sqrt[p]{\sum_{l=1}^d(x_{il}-x_{jl})^2} D(Xi,Xj)=p∑l=1d(xil−xjl)2
从式中可以看出,若p为无穷大时,这种距离可以称为切比雪夫距离;若p=2时就是欧几里得距离;那么当p=1时就是曼哈顿距离。
5,马氏距离
马氏距离是一种关于协方差矩阵的距离度量表示方法,其公式为:
D ( X i , X j ) = ( X i − X j ) T S − 1 ( X i − X j ) D(X_i,X_j)=\sqrt{(X_i-X_j)^TS^{-1}(X_i-X_j)} D(Xi,Xj)=(Xi−Xj)TS−1(Xi−Xj)
其中T表示转置,S为样本协方差矩阵。马氏距离的优点是距离与属性的量纲无关,并排除了属性之间的相关性干扰,若各个属性之间独立同分布,则协方差矩阵为单位矩阵。这样,平方马氏距离也就转化成了欧氏距离。
6,对称点距离
当聚类存在对称模式时,就可以使用对称点距离。其距离公式为:
D ( X i , X r ) = m a x j = 1 , 2 , … , N , j ≠ i ∣ ∣ ( X i − X r ) + ( X j − X r ) ∣ ∣ ∣ ∣ ( X i − X r ) ∣ ∣ + ∣ ∣ ( X j − X r ) ∣ ∣ D(X_i,X_r)=max_{j=1,2,…,N,j≠i}\frac{||(X_i-X_r)+(X_j-X_r)||}{||(X_i-X_r)||+||(X_j-X_r)||} D(Xi,Xr)=maxj=1,2,…,N,j=i∣∣(Xi−Xr)∣∣+∣∣(Xj−Xr)∣∣∣∣(Xi−Xr)+(Xj−Xr)∣∣
对称点距离就是该点到对称点和其他点距离的最小值。
7,相关系数
距离度量也可以源于相关系数,如皮尔逊相关系数的定义为:
ρ x i x j = C o v ( X i , X j ) D ( X i ) D ( X j ) ρ_{x_ix_j}=\frac{Cov(X_i,X_j)}{\sqrt{D(X_i)}\sqrt{D(X_j)}} ρxixj=D(Xi)D(Xj)Cov(Xi,Xj)
8,余弦相似度
最后一种直接计算相似性的方法是余弦相似度。其表示形式为:
S ( X i , X j ) = c o s α = X i T X j ∣ ∣ X i ∣ ∣ ∣ ∣ X j ∣ ∣ S(X_i,X_j)=cosα=\frac{X_i^TX_j}{||X_i||\ ||X_j||} S(Xi,Xj)=cosα=∣∣Xi∣∣ ∣∣Xj∣∣XiTXj
这里,S表示样本之间的相似性(以下同)。在特征空间中,两个样本越相似,则他们越趋向于平行,那么他们的余弦值也就越大。
(附:为什么大模型每个层之间要加入Layer Normalization?原因就是因为神经网络的基本计算就是点积相似度计算,而点积相似度的取值范围是没有约束的,这导致神经网络结构很难学习,因为variance太大了。所以引入Layer Normalization之后,可以让点积相似度变成了余弦相似度。当然中间有一个系数就是根号的输入向量的维度,这也就是为什么transformer架构中为什么要除以根号的输入向量的维度的原因,因为除以根号的输入向量的维度之后,Norm之后的向量,神经元的点积相似度就等于余弦相似度了。所以,让没有取值范围约束的点积相似度有了约束,【-1,1】,从而可以让神经网络稳定的训练。)
需要注意的是最后三类相似度计算方法不再符合对称性,非负性与反身性的要求,即属于非可度量的范畴。连续性变量的相似性度量方法在不同聚类算法中的应用如下图所示。