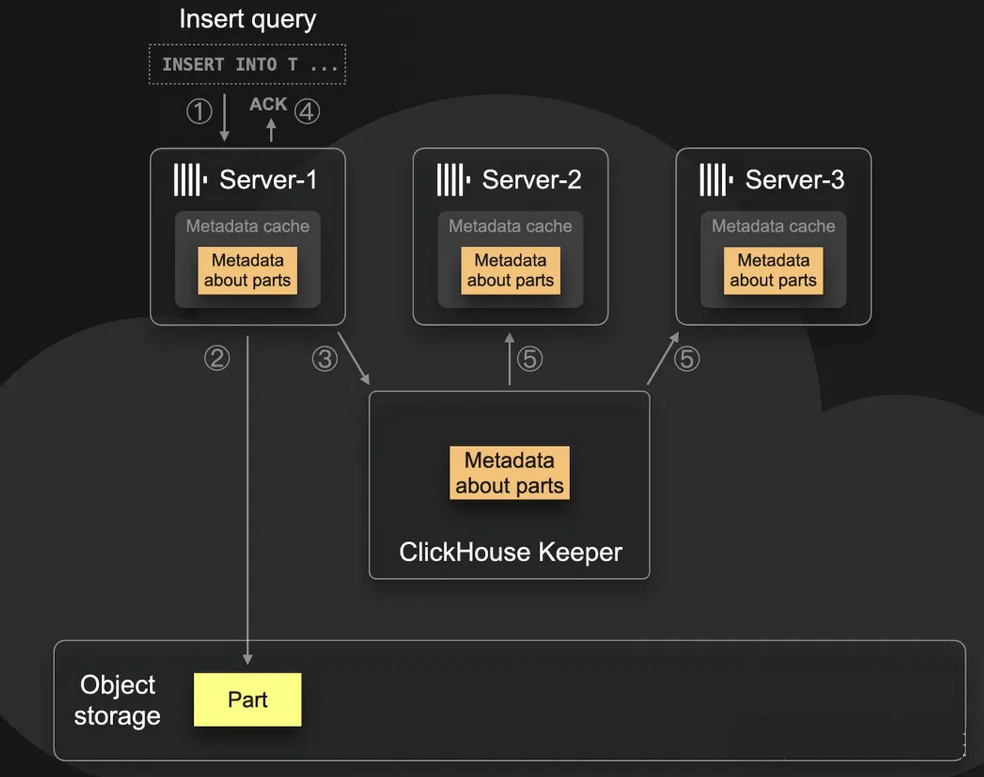
训练情况
赛后反思
幽默A题WA了两发,B题在努力回忆set里面怎么upper_bound,开完两道就在罚坐了
A题
简单的性质:偶数+偶数=偶数,奇数+奇数=偶数,奇数+偶数=奇数,每次除完保证是奇数,所以我们只需要把偶数扔到第一个,接下来全部是奇数,答案是奇数个数加一,如果没有奇数,可以用两个奇数凑出偶数,答案是奇数个数减一
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define endl '\n'using namespace std;void solve(){int n; cin>>n;vector<int> a(n + 1);int ji = 0,ou = 0;for(int i = 1;i<=n;i++){cin>>a[i];if(a[i]&1) ji++;else ou++;}if(ou) cout<<ji+1<<endl;else cout<<ji-1<<endl;
}signed main(){int T; cin>>T; while(T--)solve();return 0;
}
B题

我们把等腰梯形的上底设为 \(a\),下底设为 \(b\),腰设为 \(c\),我们想要等腰梯形存在,\(b-2c<a\),不满足这个条件的就不是等腰梯形,移项得 \(c > \frac{b-a}{2}\),我们想要找到至少一组边,所以 \(b-a\) 就得尽可能小才能找到更多的 \(c\),我们将边按照边长排序,相邻两条边的差值就是最小了,接下来我们就是找大于 \(\frac{b-a}{2}\) 的 \(c\),我们记录边的出现次数,再用一个 set 维护出现次数 \(\ge 2\) 的边,然后我们判断时对 set 进行 upper_bound 二分查找看是否存在 \(c\),若存在直接输出,如果都没有的话输出 -1
点击查看代码
#include <bits/stdc++.h>
// #define int long long
#define endl '\n'using namespace std;void solve(){int n; cin>>n;vector<int> a(n + 1);map<int,int> v;set<int> s;for(int i = 1;i<=n;i++){cin>>a[i];v[a[i]]++;if(v[a[i]] >= 2) s.insert(a[i]);}sort(a.begin() + 1,a.end());for(int i = 2;i<=n;i++){v[a[i]]--,v[a[i-1]]--;if(v[a[i]] < 2) s.erase(a[i]);if(v[a[i-1]] < 2) s.erase(a[i-1]);if(s.upper_bound((a[i] - a[i-1]) / 2.0) != s.end()){int x = *s.upper_bound((a[i] - a[i-1]) / 2.0);cout<<a[i]<<" "<<a[i-1]<<" "<<x<<" "<<x<<endl;return;}v[a[i]]++,v[a[i-1]]++;if(v[a[i]] >= 2) s.insert(a[i]);if(v[a[i-1]] >= 2) s.insert(a[i-1]);}cout<<-1<<endl;
}signed main(){int T; cin>>T; while(T--)solve();return 0;
}