数字电路设计——加法器

半加器

半加器只有两个一位宽的输入 $a$ 和 $b$ ，输出 $a+b$ 所产生的本位和 $sum$ 和进位 $cout$。组合逻辑为：

$$S=A\oplus B,Cout=AB$$

真值表和原理图符合为：

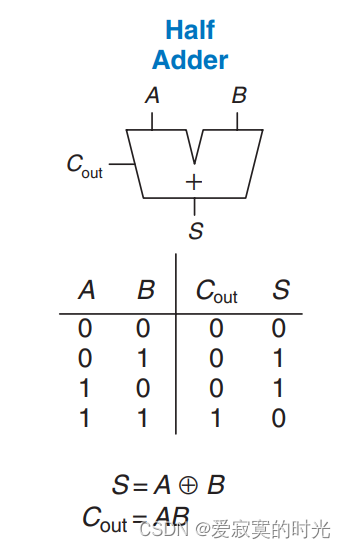
SystemVerilog实现代码：

module hadder (input logic a,input logic b,output logic sum,output logic cout
);assign sum = a ^ b;assign cout = a & b;
endmodule

全加器

加法器一般指全加器，半加器只能实现一位加法，而全加器才能真正实现多位加法，相较于半加器，全加器考虑了上一位的进位，因此全加器有三个输入分别是 $a,b,cin$ ，输出 $a+b+cin$ 所产生的本位和 $sum$ 和进位 $cout$。组合逻辑为：

$$S=A\oplus B\oplus Cin,Cout=AB+ACin+BCin$$

真值表和原理图符号为：

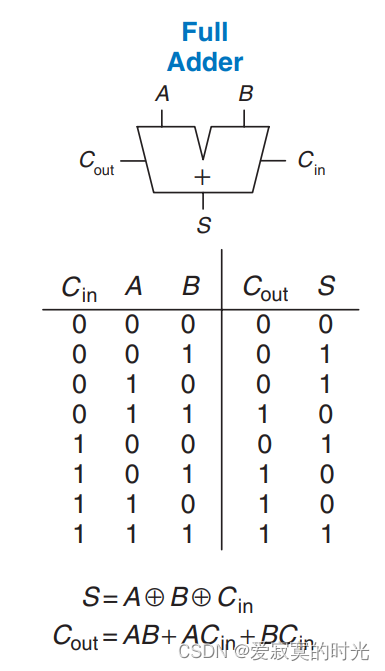
SystemVerilog实现代码：

module fadder (input logic a,input logic b,input logic cin,output logic sum,output logic cout
);assign sum = a ^ b ^ cin;assign cout = a & b | a & cin | b & cin;
endmodule

进位传播加法器

单个全加器只能实现单个位的加法，若想实习多位加法，就必须考虑到位于位直接的进位问题，我们称这类模拟竖式依次进位的加法器为进位传播加法器（carry propagate adder），简称CPA。

其原理图表示为：

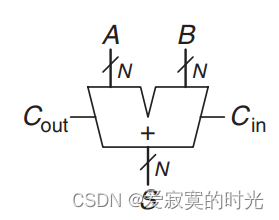
进位链加法器

单个全加器只能实现单个位的加法，当将多个全加器进行进位链式连接的时候，就可以实现多位加法，我们称为进位链加法器（Ripple-Carry Adder），具体的，一个32位宽的进位链加法器可表示为：

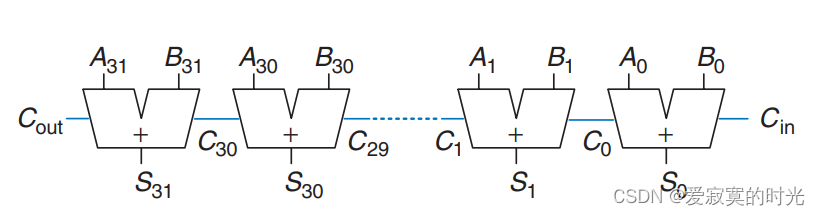
SystemVerilog实现代码：

module rcadder(input logic[31:0] a,input logic[31:0] b,input logic cin,output logic[31:0] sum,output logic cout
);genvar i;
logic[32:0] c;generateassign c[0] = cin;for(i = 0;i < 32;i=i+1) beginfadder adder_inst(.a (a[i]),.b (b[i]),.cin (c[i]),.sum (sum[i]),.cout (c[i + 1]));end
endgenerateassign cout = c[32];endmodule

显然，进位加法器的传播延迟 $t_{ripple}$ 为：

$$t_{ripple}=N{t}_{FA}$$

其中 $N$ 为加法位宽，而 $t_{FA}$ 是单个全加器的传播延迟。

超前进位加法器

进位链加法器的缺点在于进位传播的太慢，以至于进位链成为组合逻辑的关键路径，拖慢了系统时钟速率，通过巧妙的构造，可以加速这个过程，称为超前进位加法器（Carry-Lookahead Adder），简称CLA。

CLA使用生成（generate）G和传播（propagate）P两个信号来描述一个加法器如何控制进位的输入和输出。

具体的，考虑第 $i$ 位全加器，我们称其生成进位而与上一位的进位无关，当且仅当 $A_i$ 和 $B_i$ 都是1，换句话说当 $A_i$ 和 $B_i$ 都是1的时候，该位一定进位而与上一位是否进位无关。

考虑第 $i$ 位全加器，我们称其传播进位，则当上一位进位的时候，该位一定进位，此时 $A_i$ 和 $B_i$ 有一个至少是1。

两个信号的逻辑表达式为：

$$G_i=A_i{B}_i,P_i=A_i+B_i$$

现在我们再考虑当前进位 $C_i$ 和上一位进位的关系 $C_{i-1}$ 根据G和P的定义，显然有：

$$C_i=G_i+P_i{C}_{i-1}$$

现在来考虑一个进位链加法器，我们将 $G_{i:j}$ 表示为第j个到第i个加法器所组成CPA的G信号，而将 $P_{i:j}$ 表示为第j个到第i个加法器所组成CPA的P信号。

具体的，考虑 $G_{3:0}$ 的表示，若 $G_{3:0}$ 成立，当且仅当 $G_3$ 成立，或是 $P_3{G}_{2:0}$ 成立。那么：

$$G_{3:0}=G_3+P_3{G}_{2:0}$$

我们发现这是一个递归定义的式子，将递归展开后得到：

$$G_{3:0}=G_3+P_3(G_2+P_2(G_1+P_1{G}_0))$$

考虑 $P_{3:0}$ 的表示，其结构类似于串联的开关：

$$P_{3:0}=P_3{P}_2{P}_1{P}_0$$

而且下面的式子显然成立：

$$C_i=G_{i:j}+P_{i:j}{C}_{j-1}$$

有了上面的基础，我们就可以描述超前进位加法器的结构：

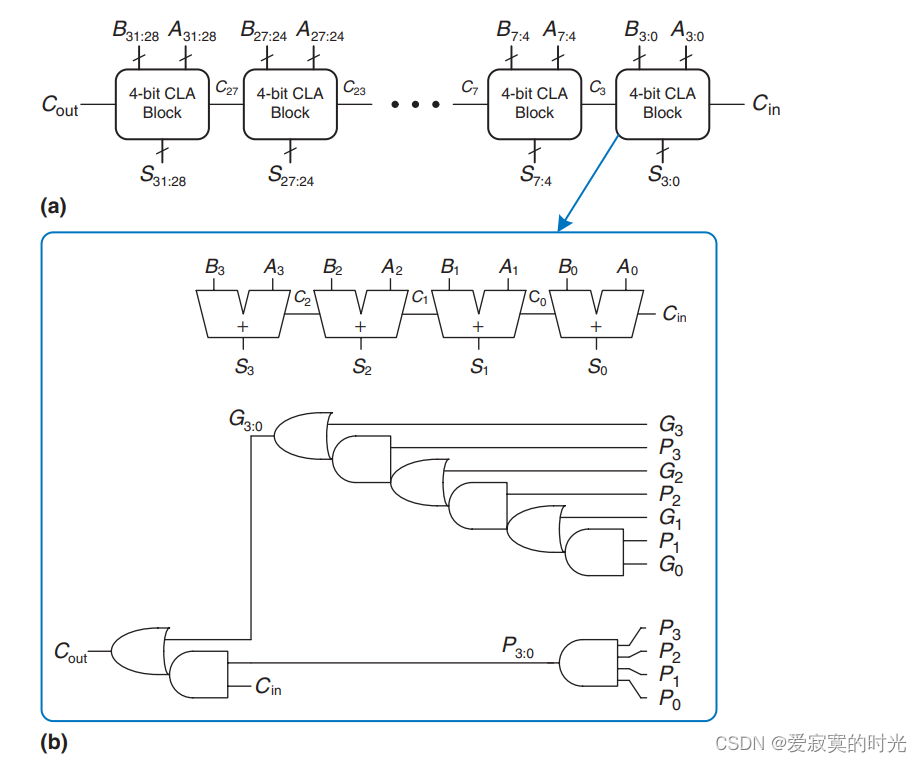
超前进位加法器利用了并行的思想，例如将32位的加法，拆成8个4位的并行加法器，每个4位加法器中仍然使用进位链加法器，不同的是，通过构造G和P，使得并行加法器之间传播进位更快了，解决了传统进位链加法器进位传播慢的特点。具体的，G和P只和当前位有关，而和进位位无关，因此对于G和P的计算结构是并行的。

一旦所有并行加法器的 $G_{i:j}$ 和 $P_{i:j}$ 同时计算好之后，$C$ 进位就可以快速的传播，只需要串行传播8次即可，相比于进位链加法器传播32次少了不少。下面是超前进位加法器的时间线：

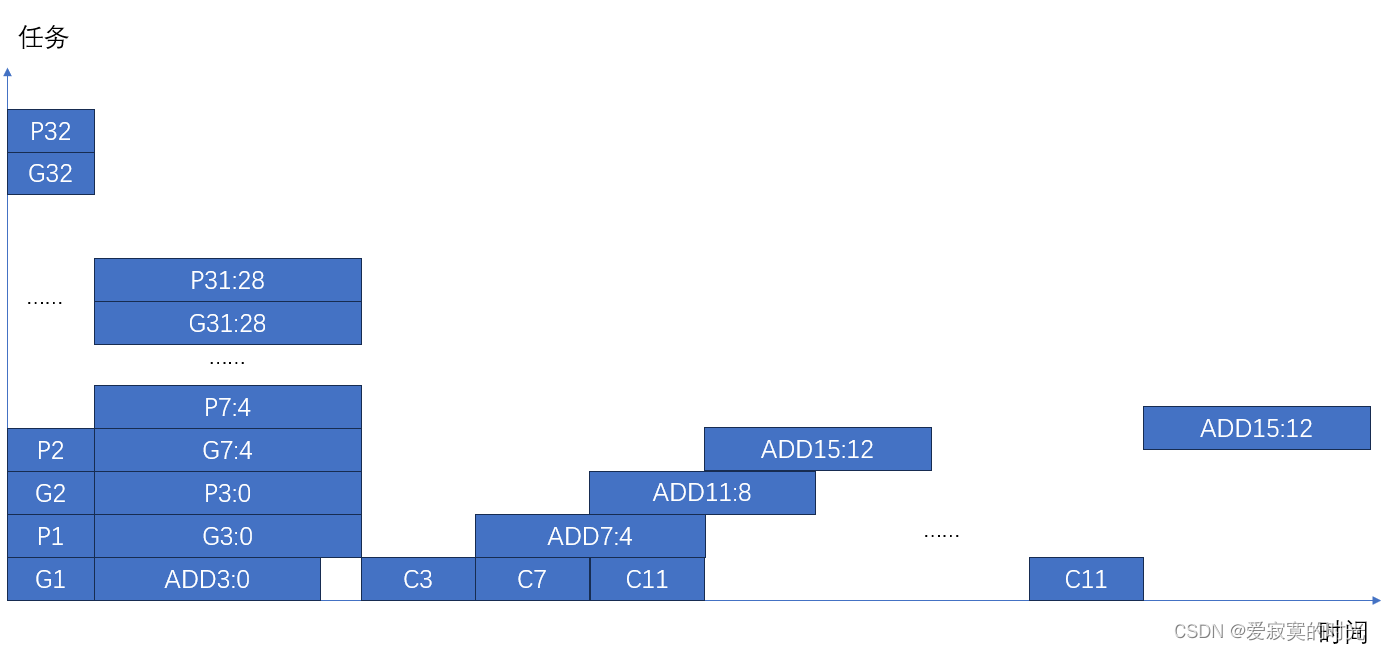
观察可以得到，超前进位加法器的传播延迟为：

$$t_{CLA}=t_{pg}+t_{pgblock}+(\frac{N}{k}-1)t_{AND/OR}+k{t}_{FA}$$

其中 $t_{pg}$ 是计算单个 $G_i$ 和 $P_i$ 的时间，通常是一个与门或是或门的传播时延。 $t_{pgblock}$ 是计算单个并行加法器的G和P的时间， $N$ 是加法器的位数， $k$ 的每个并行加法器的位数， $t_{AND/OR}$ 是从 $C_i$ 到 $C_{i+k}$ 的时延，通常为一个或门加与门的传播时延。 $k{t}_{FA}$ 是一个并行加法器的加法的传播时延。

当 $N>16$ 的时候，超前进位加法器的时延将远大于进位链加法器。

SystemVerilog实现代码：

module rcadder4(input logic[3:0] a,input logic[3:0] b,input logic cin,output logic[3:0] sum,output logic cout
);genvar i;
logic[4:0] c;generateassign c[0] = cin;for(i = 0;i < 4;i=i+1) beginfadder adder_inst(.a (a[i]),.b (b[i]),.cin (c[i]),.sum (sum[i]),.cout (c[i + 1]));end
endgenerateassign cout = c[4];
endmodulemodule cladder(input logic[31:0] a,input logic[31:0] b,input logic cin,output logic[31:0] sum,output logic cout
);genvar i;
logic[31:0] g;
logic[31:0] p;
logic[8:0] c;generateassign c[0] = cin;for(i = 0;i < 32;i=i+1) beginassign g[i] = a[i] & b[i];assign p[i] = a[i] | b[i];endfor(i = 0;i < 8;i=i+1) beginlogic g_block;logic p_block;assign g_block = g[i * 4 + 3] | p[i * 4 + 3] & (g[i * 4 + 2] | p[i * 4 + 2] & (g[i * 4 + 1] | p[i * 4 + 1] & g[i * 4]));assign p_block = p[i * 4 + 3] & p[i * 4 + 2] & p[i * 4 + 1] & p[i * 4];assign c[i + 1] = g_block | p_block & c[i];rcadder4 adder4_inst(.a (a[(i + 1) * 4 - 1:i * 4]),.b (b[(i + 1) * 4 - 1:i * 4]),.cin (c[i]),.sum (sum[(i + 1) * 4 - 1:i * 4]),.cout ());end
endgenerateassign cout = c[8];
endmodule

并行前缀和加法器

考虑如何合并两个CLA的G和P信号：

$$G_{i:j}=G_{i:k}+P_{i:k}{G}_{k-1:j},P_{i:j}=P_{i:k}{P}_{k-1:j}$$

我们将这样的组合逻辑元件记为：

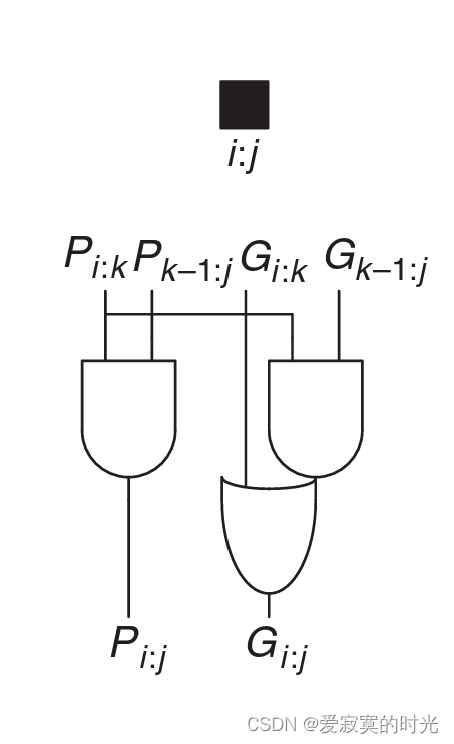
考虑到第$i$个全加器的进位为 $C_i$ 特别的 $C_0=Cin$ 。那么：

$$C_i=G_{i-1:0}+P_{i-1:0}Cin$$

那么 $C_i$ 只和 $G$ 和 $P$ 的前缀和有关系。有很多并行计算前缀和的结构，其中我们介绍Ladner-Fischer（LF）结构如下：

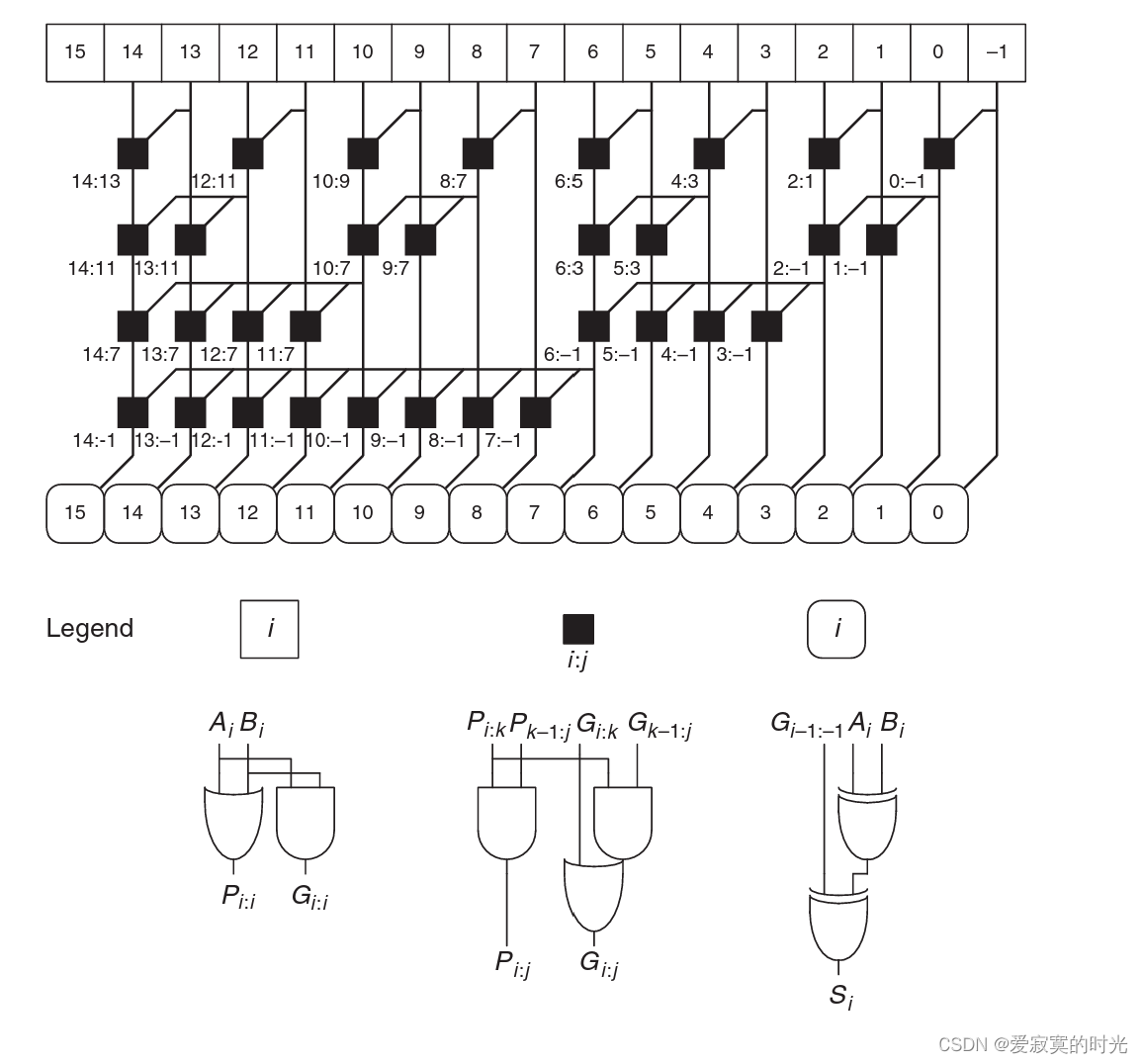
具体的，LF结构的层数是 ${\log }_{2}N$ 这里 $N$ 是加法器的位数，我们将第一个元素下标记为 $0$ ，那么第$e$层（从1开始）第$i$个元素的值 $g[e][i]$ 代表：

$$g[e][i]=G_{i:i\&\sim ((1<<e)-1)}$$

同理 $p[e][i]$ 也成立。

那么本位和就等于：

$$S[i]=A[i]\oplus B[i]\oplus C[i]$$

SystemVerilog代码实现：

module gp(input logic gh,input logic ph,input logic gl,input logic pl,output logic g,output logic p
);assign g = gh | ph & gl;assign p = ph & pl;
endmodulemodule padder(input logic[31:0] a,input logic[31:0] b,input logic cin,output logic[31:0] sum,output logic cout
);  genvar i;genvar j;genvar e;logic[31:0] g[5:0];logic[31:0] p[5:0];generatefor(i=0;i<32;i=i+1) beginassign g[0][i] = a[i] & b[i];assign p[0][i] = a[i] | b[i];endfor(e = 1;e < 6;e=e+1) beginfor(i=0;i< 32 / (1 << (e-1));i=i+1) beginif(i % 2 == 1) beginfor(j=i*(1 << (e-1));j<(i+1)*(1 << (e-1));j++) begingp gp_inst(g[e-1][j],p[e-1][j],g[e-1][i*(1 << (e-1)) - 1],p[e-1][i*(1 << (e-1)) - 1],g[e][j],p[e][j]);endendelse beginfor(j=i*(1 << (e-1));j<(i+1)*(1 << (e-1));j++) beginassign g[e][j] = g[e-1][j];assign p[e][j] = p[e-1][j];endendendendassign sum[0] = a[0] ^ b[0] ^ cin;for(i=1;i<32;i++) beginassign sum[i] = a[i] ^ b[i] ^ (g[5][i-1] | p[5][i-1] & cin);endassign cout = g[5][31] | p[5][31] & cin;endgenerate
endmodule

传播延迟为：

$$t_{PA}=t_{pg}+{\log }_{2}N(t_{pgprefix})+t_{XOR}$$

其中 $t_{pg}$ 是计算一个 $G_i,P_i$ 的时间， $t_{pgprefix}$ 是合并一个G和P的时间， $t_{XOR}$ 是最后计算一个本位和的时间。