哈夫曼树

哈夫曼树的基本介绍

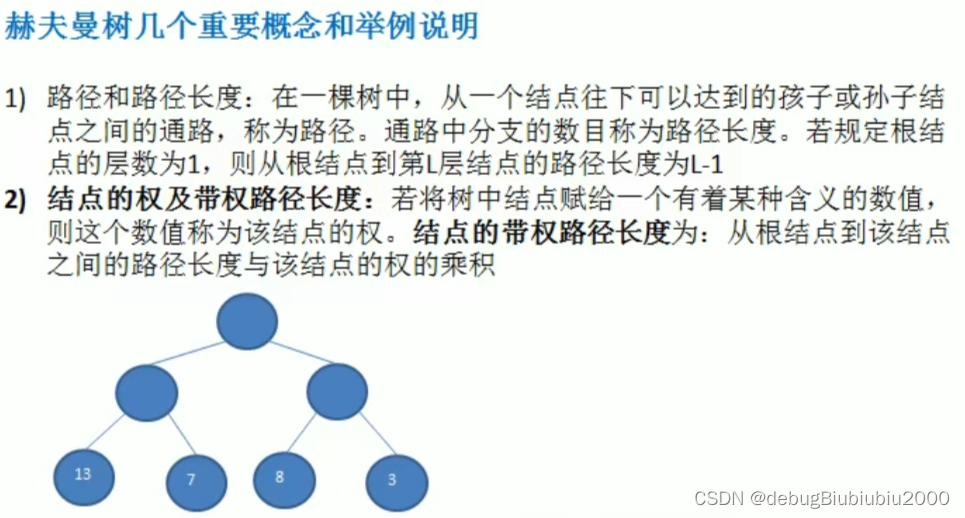
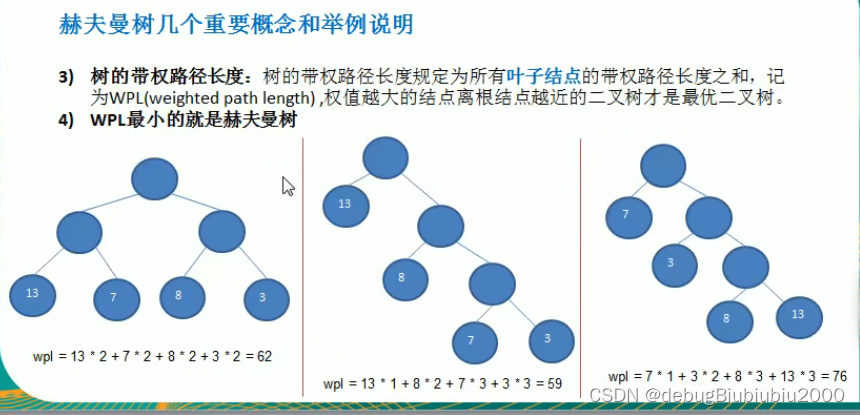
哈夫曼树构建步骤图解

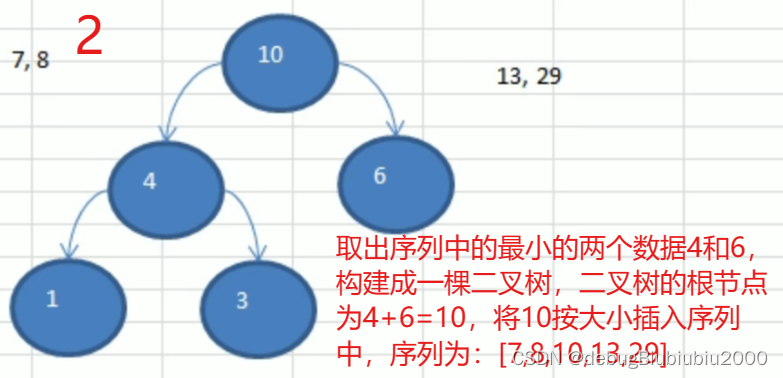
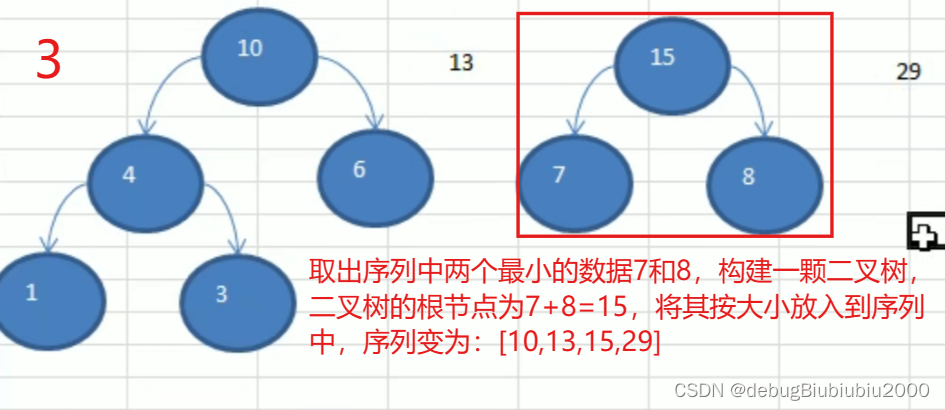
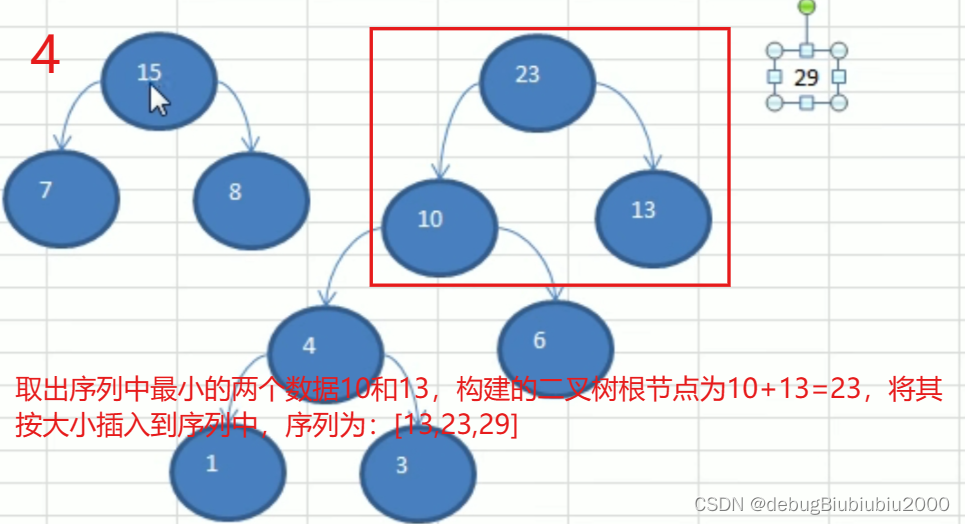
创建哈夫曼树代码实现

""" 创建哈夫曼树 """
class EleNode:""" 节点类 """def __init__(self, value: int):self.value = valueself.left = None  # 指向左子节点self.right = None  # 指向右子节点def __str__(self):return f"Node [value={self.value}]"def pre_order(self):"""前序遍历二叉树"""if self is None:return# 先输出父节点print(self, end=' => ')# 左子树不为空则递归左子树if self.left is not None:self.left.pre_order()# 右子树不为空则递归右子树if self.right is not None:self.right.pre_order()class HuffmanTree:arr: list = Nonedef __init__(self, arr):self.arr = arrdef create_huffman_tree(self) -> EleNode:# 对 arr 列表进行升序排序self.arr.sort()# 遍历数组，将每个数组元素构建成一个 Node 节点# 将 Node 节点加入到一个新列表中node_list = []for i in self.arr:node_list.append(EleNode(i))# 循环进行以下步骤，直到列表中只剩下一棵二叉树，此时该二叉树就是哈夫曼树while len(node_list) > 1:# 取出权值序列中最小的两课二叉树（即列表中的前两个元素）构建一棵新的二叉树left = node_list.pop(0)right = node_list.pop(0)# 新二叉树的根节点的权值=两个节点权值之和parent = EleNode(left.value + right.value)# 让新二叉树的左右节点分别指向两个最小的节点parent.left = leftparent.right = right# 将新二叉树根据根节点的大小插入到序列中的指定位置i = 0n = len(node_list)while i < n:if node_list[i].value >= parent.value:node_list.insert(i, parent)  # 找到了根节点存放的位置breaki += 1else:# 循环结束表示新的二叉树的权值最大，在node_list列表中没有比它大的# 所以添加到列表最后node_list.append(parent)# 此时列表中只有一棵二叉树，即所求的哈夫曼树# 返回哈夫曼树的根结点return node_list[0]huffman = HuffmanTree([13, 7, 8, 3, 29, 6, 1])
node = huffman.create_huffman_tree()
node.pre_order()

哈夫曼编码

基本介绍

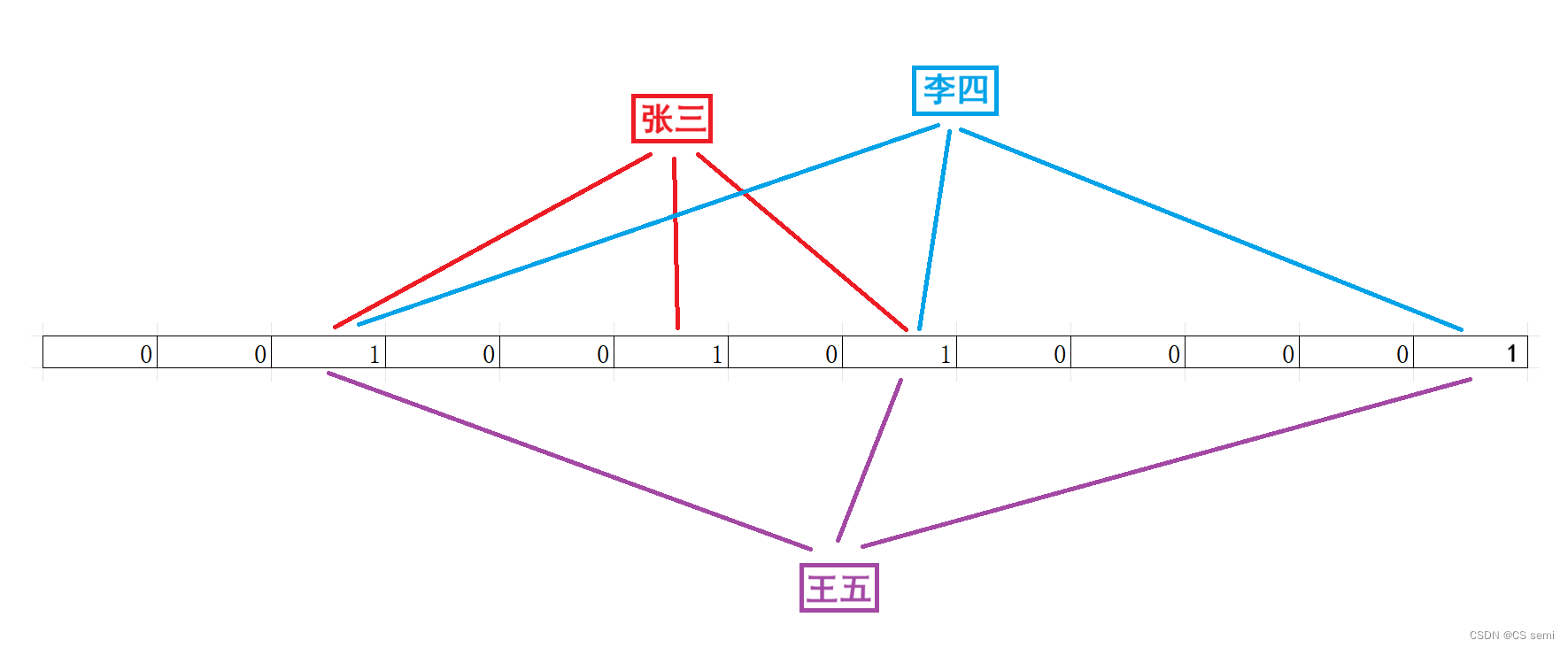
哈夫曼编码原理剖析

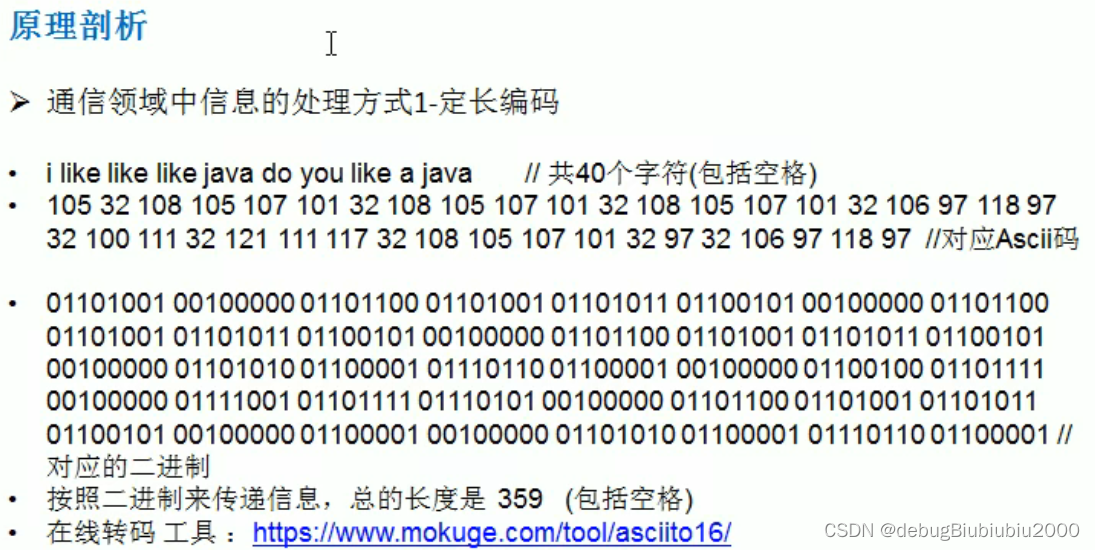
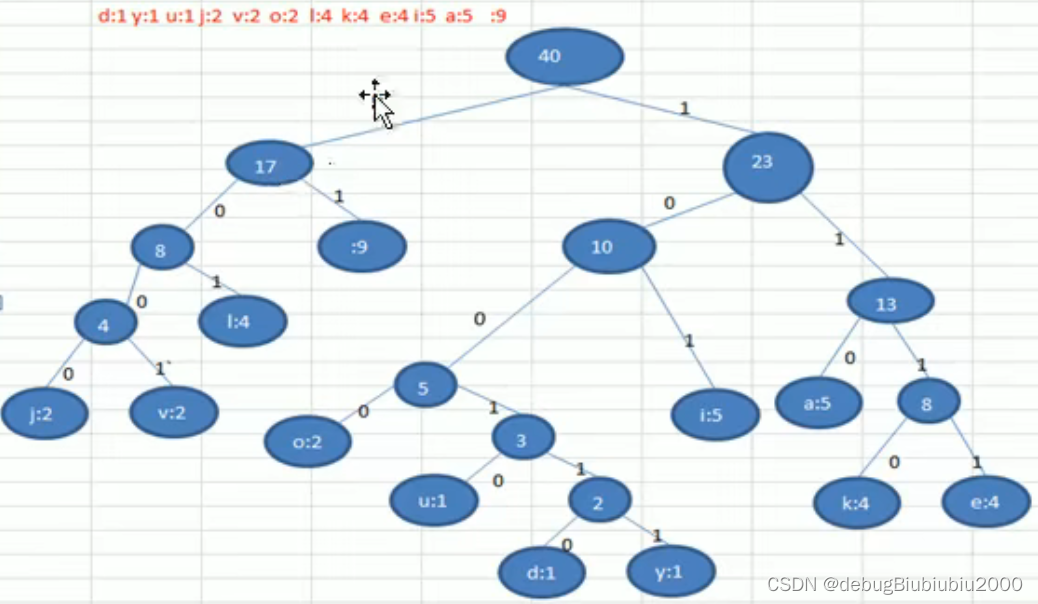
哈夫曼编码的实例

思路分析

代码实现

""" 哈夫曼编码 """
class CodeNode:def __init__(self, data: int, weight: int):self.data = data  # 存放字符对应的ASCII码值self.weight = weight  # 存放字符在字符串中出现的次数self.left = Noneself.right = Nonedef __str__(self):return f"Node[data={chr(self.data) if self.data else None}, weight={self.weight}]"def pre_order(self):"""二叉树的前序遍历"""print(self)if self.left:self.left.pre_order()if self.right:self.right.pre_order()class HuffmanCode:# 哈夫曼编码表# 存储每个字符对应的编码# key为对应的字符，val为字符对应的编码huffman_code_tab = {}# 记录哈夫曼二进制编码字符串最后一个段的长度# 即会将哈夫曼二进制字符串按八位进行分割，分割到最后一个时长度可不为8# 所以用一个变量存储最后一段二进制字符串的长度，在解码的时候会用到last_char_len = 0def create_huffman_tree(self, s: str) -> CodeNode:"""构建哈夫曼编码二叉树:param s: 要编码的字符串:return:"""# 遍历字符串，统计每一个字符出现的次数，并将结果放入字典kw = {}for ch in s:ascii_code = ord(ch)if kw.get(ascii_code):  # 如果该字符出现过，则直接将其次数加1kw[ascii_code] += 1else:  # 如果没出现过，则出现次数为1kw[ascii_code] = 1# 按照字符出现的次数对字典进行排序kw = sorted(kw.items(), key=lambda kv: (kv[1], kv[0]))# 遍历字典，将每个元素构建成一个 Node 节点# 将 Node 节点加入到一个新列表中node_list = []for k, v in kw:# print(chr(k),'=', v, end=', ')node_list.append(CodeNode(k, v))# 循环进行以下步骤，直到列表中只剩下一棵二叉树，此时该二叉树就是哈夫曼树while len(node_list) > 1:# 取出权值序列中最小的两课二叉树（即列表中的前两个元素）构建一棵新的二叉树left = node_list.pop(0)right = node_list.pop(0)# 新二叉树的根节点的权值=两个节点权值之和parent = CodeNode(None, left.weight + right.weight)# 让新二叉树的左右节点分别指向两个最小的节点parent.left = leftparent.right = right# 将新二叉树根据根节点的大小插入到序列中的指定位置n = len(node_list)i = 0while i < n:if node_list[i].weight >= parent.weight:node_list.insert(i, parent)  # 找到了根节点存放的位置breaki += 1else:# 循环结束表示新的二叉树的权值最大，在node_list列表中没有比它大的# 所以添加到列表最后node_list.append(parent)# 此时列表中只有一棵二叉树，即所求的哈夫曼树# 返回哈夫曼树的根结点return node_list[0]def get_huffman_code_tab(self, ele_node: CodeNode, code: str, code_str: str):"""遍历所创建的哈夫曼树，得到所有叶子节点（叶子结点即要得到的字符）的编码这里规定左节点为0，右节点为1:param ele_node: 传入的要遍历的树的根节点，初始为根节点:param code: 表示所选择的路径是左节点还是右节点:param code_str: 每个字符对应的编码:return:"""code_str += code  # 拼接编码if ele_node.data is None:# 表示是非叶子节点，因为在创建哈夫曼树时设置了为叶子结点的data为空# code_str += codeif ele_node.left:self.get_huffman_code_tab(ele_node.left, '0', code_str)if ele_node.right:self.get_huffman_code_tab(ele_node.right, '1', code_str)else:  # 是叶子节点self.huffman_code_tab[chr(ele_node.data)] = code_strdef huffman_zip(self, s: str) -> list:"""利用哈夫曼编码表把字符串中的每一个字符转换成对应的编码即将一个字符串根据哈夫曼编码进行压缩，得到一个压缩后的结果:param s: 要转换的字符串:return: 返回编码后的列表"""res = ''# 遍历字符串，将每一个字符转换成对应的编码，并将所有编码拼接起来# "i like like like java do you like a java" => 以下形式# 1100111111101110001011111110111000101111111011100010100001011000101011# 001100001011001000011001110111111101110001011010100001011000101for i in s:res += self.huffman_code_tab[i]# 将得到的编码字符串按八位进行分割，将每八位转换成一个int，并将int存放到列表中code_list = []i = 0n = len(res)while i < n:num = int(res[i:i + 8], 2)  # 将二进制字符串转换为整数code_list.append(num)i += 8if i < n <= i + 8:  # 已经分割到了最后一部分，记录该部分的长度self.last_char_len = n - ireturn code_listdef huffman_decode(self, code_list) -> str:"""将哈夫曼编码进行解压，得到一个可阅读的字符串:param code_list: 要解压的哈夫曼编码列表:return: 解码后的字符串"""# 将哈夫曼编码列表转换成对应的二进制字符串# [415, 476, 95, 476, 95, 476, 80, 177, 345, 389, 400, 206, 254, 226, 212, 44, 5] =># 1100111111101110001011111110111000101111111011100010100001011000101011# 001100001011001000011001110111111101110001011010100001011000101code_str = ''  # 存储对应的二进制字符串count = 0n = len(code_list)for i in code_list:t = "{:08b}".format(i)  # 将整数转换为二进制字符串code_str += tcount += 1if count == n - 1:breakcode_str += "{:0{k}b}".format(code_list[count], k=self.last_char_len)# 将哈夫曼编码表的键值互换# 比如原来的是'a': '001' => 变成 '001': 'a'code_tab = {}for k, v in self.huffman_code_tab.items():code_tab[v] = k# 遍历二进制字符串j = 0i = 1n = len(code_str)res_code = ''  # 解码后的字符串while i <= n:t = code_str[j:i]ch = code_tab.get(t)if ch:res_code += chj = ii += 1return res_codes = "i like like like java do you like a java"
# s = "I love python hahha nihao"
huffman = HuffmanCode()
root_node = huffman.create_huffman_tree(s)
huffman.get_huffman_code_tab(root_node, '', '')
huffman_code_list = huffman.huffman_zip(s)
decode_str = huffman.huffman_decode(huffman_code_list)
print(decode_str)

使用哈夫曼编码压缩文件的注意事项（代码胜省略）