Leetcode 剑指 Offer II 050. 路径总和 III-编程知识

Leetcode 剑指 Offer II 050. 路径总和 III

题目难度: 中等

原题链接

今天继续更新 Leetcode 的剑指 Offer（专项突击版）系列, 大家在公众号 算法精选 里回复 剑指offer2 就能看到该系列当前连载的所有文章了, 记得关注哦~

题目描述

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的路径的数目。

路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：

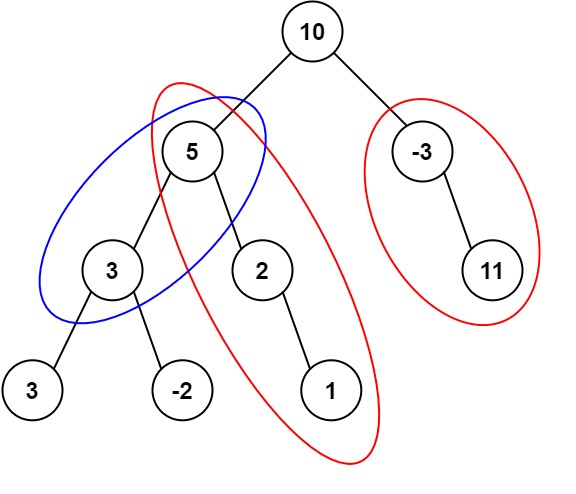
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

示例 2：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3

提示:

二叉树的节点个数的范围是 [0,1000]
-10^9 <= Node.val <= 10^9
-1000 <= targetSum <= 1000

题目思考

如何快速计算任意路径的和?
如何快速得到指定和的路径数目?

解决方案

思路

要想得到任意从上到下的路径的和, 很容易想到类似数组前缀和的做法
- 例如对于上述示例, 要想得到最右侧 4->1 的路径和, 我们可以通过计算根节点到节点 1 和节点 8 的前缀和差值来得到: sum(5->8->4->1) - sum(5->8)
通过这样预处理, 我们可以得到任意从上到下路径的和, 那如何快速得到指定和的路径数目呢?
- 我们可以额外引入一个计数字典 sumCnt, 来统计当前路径已经遍历过的所有节点的前缀和的计数, 注意初始化sumCnt[0] = 1, 代表路径没有任何节点的情况
- 在遍历当前节点时, 假设其前缀和为 curSum, 目标路径和为 targetSum, 那么以当前节点为终点的所有路径中, 路径和为 targetSum 的路径数目即为 sumCnt[curSum - targetSum], 累加所有节点的这一数目, 就得到了最终结果
下面代码中有详细的注释, 方便大家理解

复杂度

时间复杂度 O(N): 每个节点只会被遍历一次
空间复杂度 O(logN): 递归调用最多使用 O(logN) 栈空间, 而前缀和计数字典也会存当前路径上的节点, 这部分也是 O(logN)

代码

class Solution:def pathSum(self, root: TreeNode, targetSum: int) -> int:# 递归+前缀和计数字典# sumCnt是前缀和计数字典{curSum:cnt}, 统计当前路径上前缀和是curSum的路径数目cntsumCnt = collections.defaultdict(int)# 显然刚开始时就存在前缀和是0的一种情况, 即空路径sumCnt[0] = 1# res记录最终满足条件的路径数目res = 0def dfs(node, curSum):nonlocal resif not node:# 当前节点为空, 返回return# 更新当前前缀和curSum += node.val# 以当前节点为终点的满足条件的路径数目为sumCnt[curSum - targetSum], 累加到最终结果中res += sumCnt[curSum - targetSum]# 当前前缀和计数+1, 在遍历子树中可以被用到sumCnt[curSum] += 1# 继续递归左右子树dfs(node.left, curSum)dfs(node.right, curSum)# 最后恢复现场, 因为退出当前递归函数后, 当前节点就不在路径上了, 所以其计数要-1sumCnt[curSum] -= 1dfs(root, 0)return res