索引是什么?
索引是一种用于加快查询和索引的数据结构,其本质上就是一种排序好的数据结构,就类似书的目录。
索引的底层有多种实现的结构:b树,b+树,Hash,红黑树。InnoDB和MyISAM的索引都是通过b+树实现的。
索引的优缺点
优点
1.使用所以可以大大提高检索的速度(大大减少检索的数据量),这就是创建索引的主要原因。
2.我们可以创建唯一性索引,可以实现保证每行数据的唯一性。
缺点
1.创建和维护索引需要大量的时间,当对表中的数据进行增删改时如果存在索引,则也需要对索引进行修改,这会降低SQL语句的速率。
2.索引也需要物理储存,会消耗一定量的空间内存。
索引底层数据结构的选型
Hash表
使用键值对的方式储存数据,通过hash函数(通过对地址进行取模操作)计算数据储存的索引,通过索引确定位置并储存数据。
hash表存在hash值冲突的问题:两个不相同的数据可能存在相同的hash值。
为了解决这个问题,我们使用拉链法,将hash值相同的数据,在其对应的位置使用链表进行储存。

从而解决hash冲突的问题。
但是innodb没有采用hash表,因为hash表不支持顺序和范围查询,并且每次IO只能返回一个数据。
SELECT * FROM table WHERE id < 500;
如果此时索引使用的hash表的结构,那么它需要将1~499的数据使用hash函数定位出来,效率十分低下。
二叉搜索树
特点:每个节点都符合:左边节点的值都小于当前节点,右边节点的值都大于当前节点。
在理想条件下,节点的左子树的深度和右子树的深度差不会超过一层,此时的时间复杂度为O(logN),而当插入的数据为递增或递减的情况时(斜树),结构就会变成链表的结构,此时的时间复杂度为O(N),效率就大大降低。
但是innodb没有采用二叉搜索树,因为二叉搜索树极度依赖其平衡性,太不稳定了。
AVL(平衡二叉搜索树)
其结构就是一直保持左右子树的高度差为1以内的二叉搜索树。为了解 决二叉搜索树变为链表的情况。
主要通过四种旋转操作控制二叉树的平衡,LL,RR,LR,RL。
在数据的储存上需要频繁依赖旋转操作来保持平衡,需要巨大的计算开销从而影响性能,因为在每个节点上只能储存一个数据,而每次进行IO操作时只能获取一个数据,如果需要查询的数据存在于多个节点上,我们就要多次使用IO操作,非常的耗时(IO操作是非常耗时的),所以innoDB没有使用AVL作为数据结构。
红黑树
红黑树的特点:
1.节点只能为黑色或红色。
2.叶子节点为黑色。
3.根节点到各个叶子节点的黑色节点的个数是相同的。
4.根节点为黑色。
5.节点为红色,则其父节点为黑色,子节点为黑色。
红黑树的是出现就是为了解决AVL频繁旋转的问题。
因为红黑树的平衡较弱,其要求就是左右子树的高度在两倍以下,可能会导致树的高度较高,查找次数增多,可能导致一些数据需要多次IO操作才能得到,效率会变的低下,所以innoDB没有使用改数据结构。
B树和B+树(多路平衡查找树)
为了解决红黑树的高度高导致的查询速度慢的问题,我们就使用B树和B+树,它们就是多叉搜索树。
B树的特点: 在数据量相同的情况下,平衡二叉查找树的高度要大于B树的高度。
B树的结构

B+树的结构
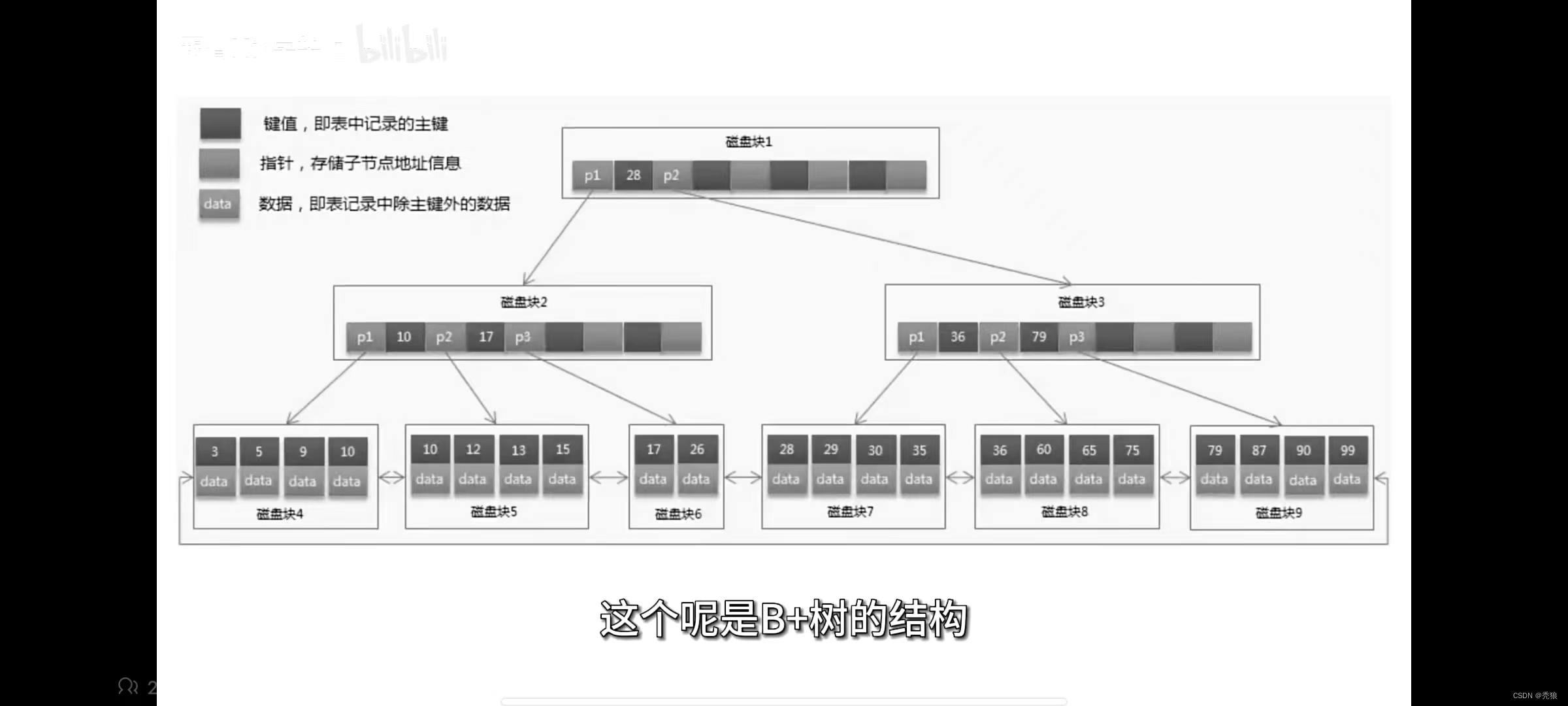
B树和B+树的区别
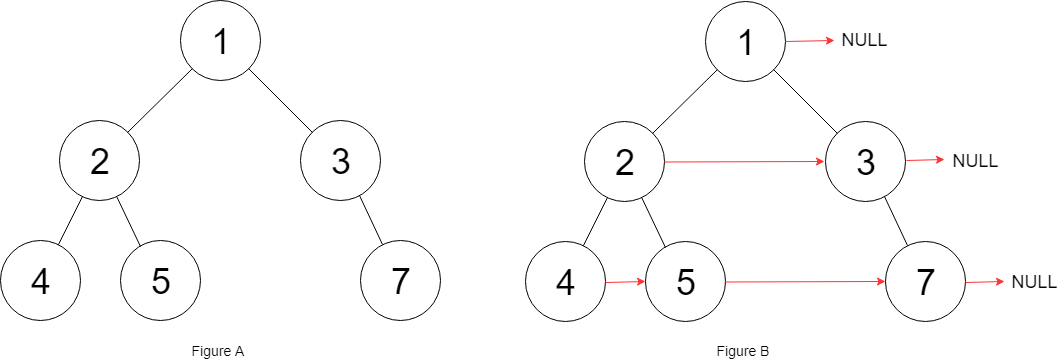
1.B树的子树数量等于关键字的数量 + 1,2.B树的叶子节点是独立的,而B+树的叶子节点则是使用双向链表进行关联的。
3.B树的所有节点都可以存放key和data,而B+树只有在叶子节点才能存放key和data。
InnoDB和MyISAM的索引为什么都是使用B+树实现的呢?
储存相同数据的时候,AVL树的高度比B树要高,所以器其对应的IO的操作次数也更多,为了减少IO的操作次数,我们使用B+树实现索引。
主索引(primary key)
主索引也叫主键。
在mysql的InnoDB中,如果在表中没有设置主键,InnoDB会自动检查表中是否有唯一索引且没有null值的字段,如果有的话,就会将该字段设置为主索引,如果没有找到自动创建一个6Byte的自增主键。
二级索引
通过二级索引,我们可以确定主键的位置,因为二级索引的叶子节点储存的数据就是主键。
二级索引有: 唯一索引,普通索引,前缀索引,全文索引。
二级索引的种类和作用
唯一索引: 唯一索引是一种约束,其的作用就是唯一索引的属性列中的数据不能重复,但是其可以为null,用于实现数据的唯一性,在一张表中可以设置到多个唯一索引。
普通索引:用于加快数据的查询速度,在一张表中可以设置多个普通索引。
前缀索引:适用于字符串类型的数据,就是去字符串前缀几个字符作为索引,比普通索引建立的数据更小。
全文索引:全文索引主要是为了检索大文件数据中的关键字的信息。
聚簇索引(聚集索引)
索引的结构和数据一起存放的索引,并不是一种单独的索引类型,InnoDB的主键就是使用聚簇索引。
聚簇索引的优缺点
优点
1.查询速度非常快:因为整个结构就是B+树,所以查询速度非常快,相比于非聚簇索引,聚簇索引少一次IO操作。
2.对排序查找和范围查找优化。
缺点
1.依赖于有序的数据:因为B+树的原因,如果数据无序的情况,在数据插入的时候需要进行排序,效率就很低。
2.更新代价大:因为结构和数据存放在一起,所以在修改的时候更新代价大。
非聚簇索引(非聚索引)
索引的结构和数据不是存放在一起的索引,并不是一种单独的索引类型,二级索引就是非簇索引,MyISAM的主键和非主键都是使用非聚簇索引。
非聚簇的优缺点
优点:更新代价比聚簇索引小。
缺点
1.依赖于有序的数据,其结构是B+树。
2.可能需要二次查询(回表):这是非聚簇索引的最大缺点,当查询到对应的指针或主键后,还需要根据指针或主键再到文件或表中查询。
非簇索引一定会进行回表吗?
不一定,当一个索引包含(覆盖)了需要查询字段的所有值的时候,就不需要进行回表操作了。
SELECT name FROM table WHERE name='guang19';
此时如果字段name正好建立了索引,此时索引包含了所有需要查询的字段,并且不会进行回表操作。
总的来说,如果一个索引包含了所有需要查询的字段的时候(也就是覆盖索引),就不需要回表操作。
覆盖索引和联合索引
覆盖索引
覆盖索引:查询的所有字段正好是索引的字段,那么直接根据索引查询出数据,无需进行回表操作。
联合索引
联合索引:使用表中多个字段创建索引,该索引就叫作联合索引或组合索引或复合索引。
索引下推
索引下推是mysql5.6之后提供的一项索引优化功能,可以在非聚簇索引遍历过程中,对索引包含的字段先进行判断,过滤不符合条件的记录,减少回表的次数。