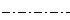1.dijkstra维护最长路

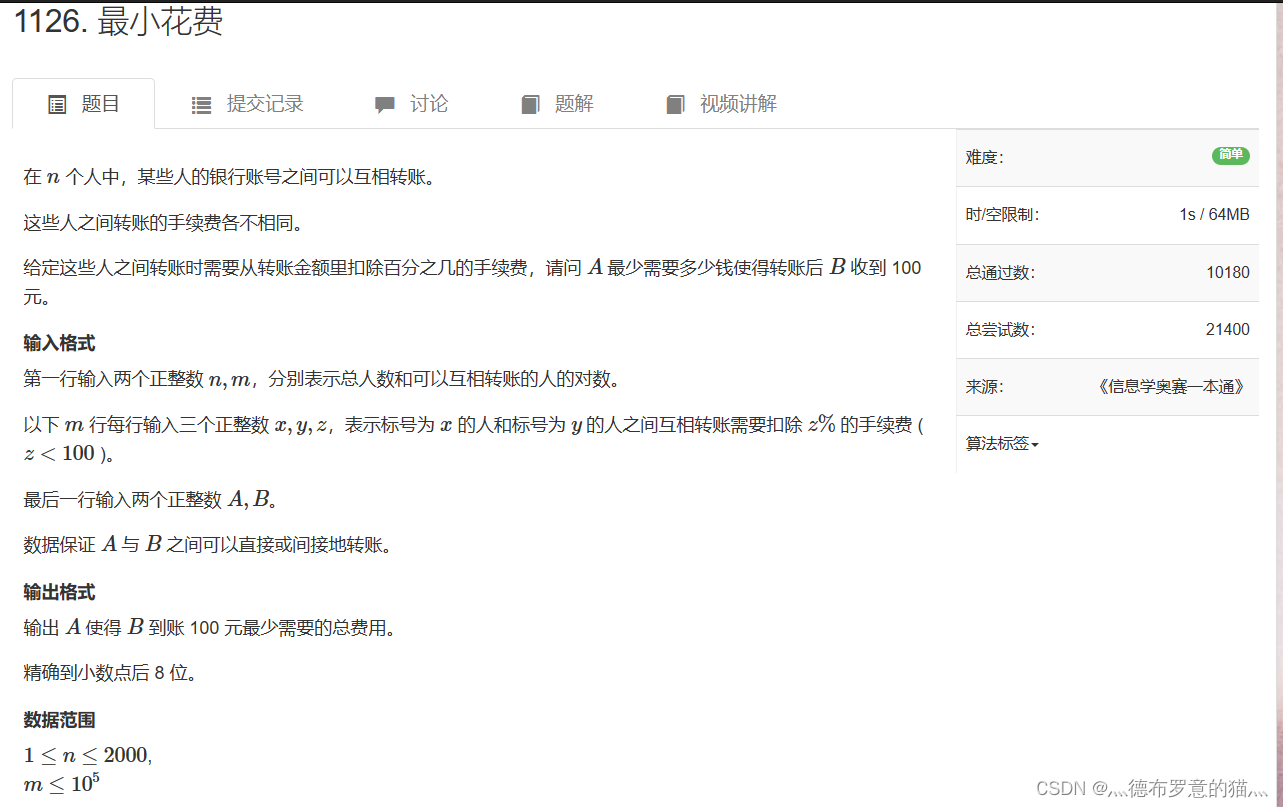
下面这个是讨论区的一个佬的理解，非常的nice

总结一句话，dijkstra的贪心保证了每次选定的点在之后都不会被其他点所更新了

同理维护最长路的时候我们发现，如果权值是0-1的话，选定的最大值在之后不会变的更大

所以可以用dijkstra来维护最长路

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
double g[2010][2010];
int n,m,s,t;
double dist[N];
bool st[N];
double dijkstra()
{dist[s] = 1.0;for(int i=1;i<=n;i++){int t = -1;for(int j=1;j<=n;j++)if(!st[j]&&(t==-1||dist[j]>dist[t]))t = j;st[t] = 1;for(int j=1;j<=n;j++)if(dist[j]<dist[t]*g[t][j])dist[j] = dist[t]*g[t][j];}return dist[t];
}int main()
{cin>>n>>m;for(int i=1;i<=m;i++){int a,b,c;cin>>a>>b>>c;double z = (100.0-c*1.0)/100.0;g[a][b] = g[b][a] = max(g[a][b],z);}cin>>s>>t;printf("%.8lf",100.0/dijkstra()*1.0);}

2.stringstream处理不定长输入

#include<bits/stdc++.h>
using namespace std;
int n,m;
const int N = 1100;
int g[N][N];
int dist[N];
int a[N];
bool st[N];void dijkstra()
{memset(dist,0x3f,sizeof dist);dist[1] = 0;for(int i=1;i<=n;i++){int  t = -1;for(int j=1;j<=n;j++)if(!st[j]&&(t==-1||dist[j]<dist[t]))t = j;st[t] = 1;for(int j=1;j<=n;j++)if(dist[j]>dist[t]+g[t][j])dist[j] = dist[t] + g[t][j];}
}int main()
{cin>>m>>n;memset(g,0x3f,sizeof g);for(int i=1;i<=n;i++)g[i][i] = 0;getchar();for(int i=1;i<=m;i++){string str;getline(cin,str);stringstream ssin(str);int k  = 1;while(ssin>>a[k])k++;k--;for(int s=1;s<=k;s++)for(int j=1;j<s;j++)g[a[j]][a[s]] = 1;}dijkstra();if(dist[n]==0x3f3f3f3f)cout<<"NO";else cout<<dist[n]-1;}

3.简单虚拟原点

注意酋长不一定是这里面等级最高的 所以我们要枚举区间算好几次dijkstra

#include<iostream>
#include<cstring>
using namespace std;const int N = 1010;
int g[N][N];
int dist[N];
bool st[N];
int m,n;
int level[N];int dijkstra(int l,int r){memset(dist,0x3f,sizeof dist);dist[0] = 0;memset(st,0,sizeof st);for(int i=1;i<=n;i++){int t = -1;for(int j=0;j<=n;j++)if(!st[j]&&(t==-1||dist[j]<dist[t]))t = j;st[t] = 1;for(int j=1;j<=n;j++)if(level[j]>=l&&level[j]<=r)dist[j] = min(dist[j],dist[t]+g[t][j]);}return dist[1];
}int main()
{cin>>m>>n;memset(g,0x3f,sizeof g);for(int i=0;i<=n;i++)g[i][i] = 0;for(int i=1;i<=n;i++){int p,l,x;cin>>p>>l>>x;level[i] = l;g[0][i] = p;for(int j=1;j<=x;j++){int a,b;cin>>a>>b;g[a][i] = min(g[a][i],b);}}int res = 0x3f3f3f3f;for(int i=level[1]-m;i<=level[1];++i)res = min(res,dijkstra(i,i+m));cout<<res;}