理解快速排序-编程知识

理解快速排序

首先了解以下快速排序

快速排序（QuickSort）是一种常用的排序算法，属于比较排序算法的一种。它是由英国计算机科学家Tony Hoare于1960年提出的，是一种分而治之（divide and conquer）的算法。

快速排序的基本思想是通过选择一个基准元素，将数组分成两个子数组，然后对这两个子数组进行递归排序。具体步骤如下：

选择基准元素： 从数组中选择一个元素作为基准元素，通常选择数组的第一个元素。
分区操作： 将数组中小于基准元素的元素移到基准元素的左边，大于基准元素的元素移到基准元素的右边。基准元素在这个过程中找到了最终的排序位置。这个操作称为分区操作。
递归排序： 对基准元素左右两侧的子数组分别进行递归排序。

这个过程递归进行，直到整个数组有序。由于快速排序采用了分治的思想，它的平均时间复杂度为O(n log n)，其中n是数组的长度。在最坏情况下，快速排序的时间复杂度为O(n^2)，但通常情况下它的性能很好，而且它是原地排序算法，不需要额外的空间。

快速排序是许多排序算法中最快的一种，它在实际应用中被广泛使用。

下面给大家画一下图来理解以下快速排序（以中间元素为基准）：

首先确定基准元素

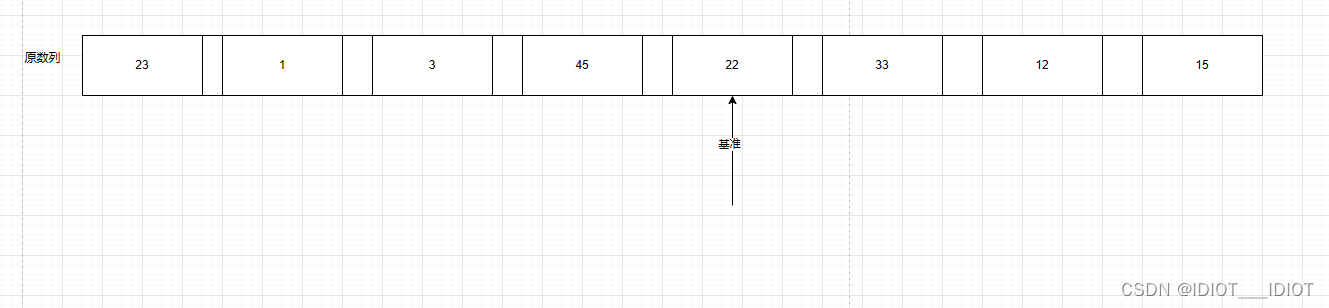
在这里插入图片描述

然后就是对序列进行遍历，如果比基准元素大的就放到右边，比基准元素小的就放到左边，确定一个变量left（排序的起点，这里为数列开始），从左边开始如果遇到一个比基准元素大的就停下，确定一个变量right（排序的终点，这里为数列结尾），从右边开始遇到一个比基准元素小的节点停止，然后交换两个停止索引的值，然后继续进行遍历，遇到上面同样的情况进行交换，如果left>right 就停止（此时第第一个分区结束），进行下一次的基准选择与分区，其实这里就是递归调用的抵挡。分为左右两边。

在这里插入图片描述

此时第一次区分结束，使得基准的左边都小于基准，右边都大于

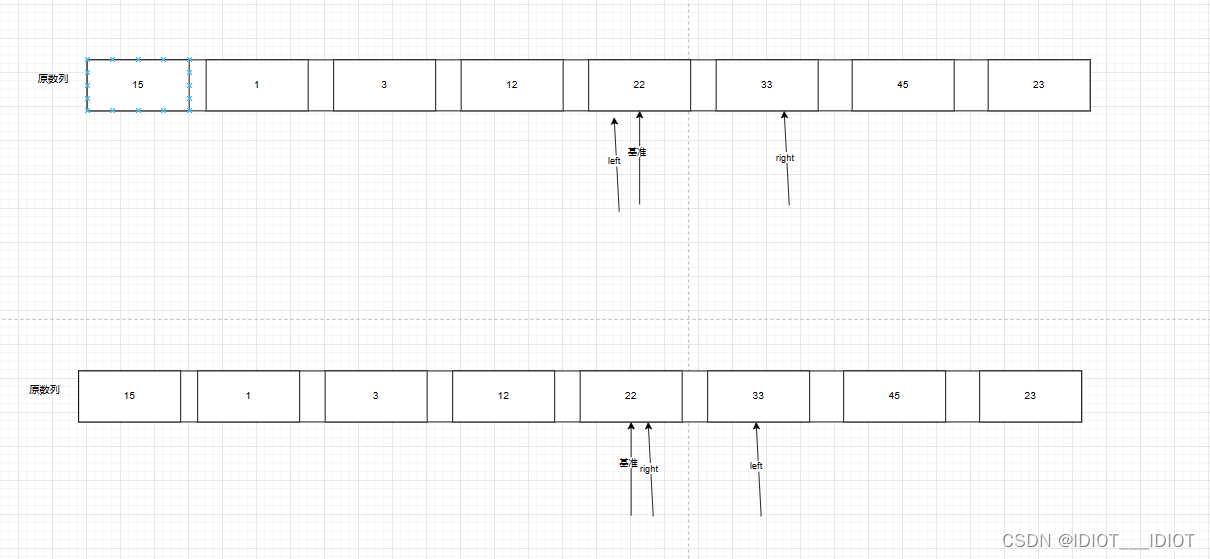
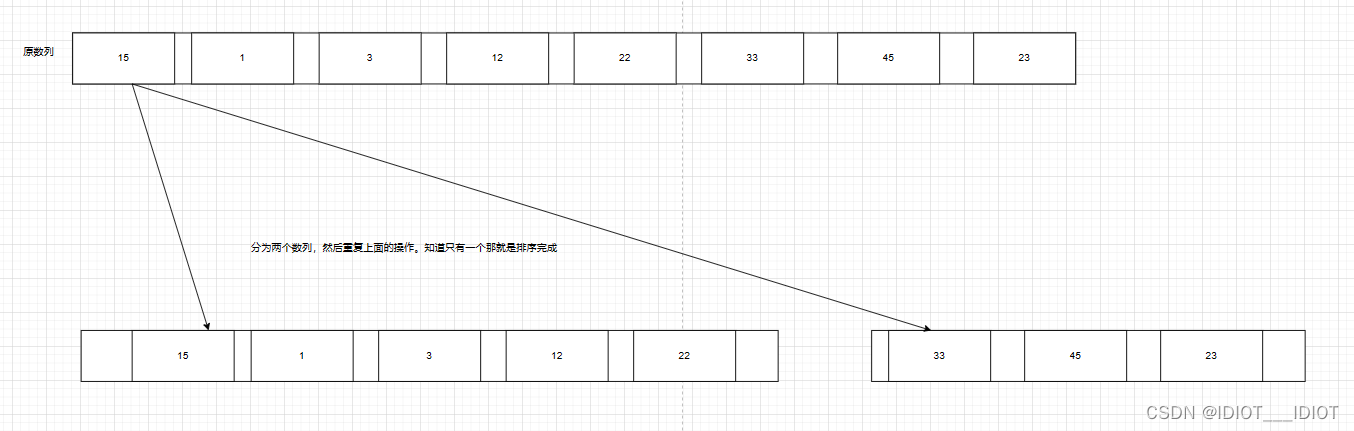
在这里插入图片描述

分为两个数列，然后重复上面的操作。知道只有一个那就是排序完成

在这里插入图片描述

代码实现

第一个版本

public static void method2(int[] arr,int left , int right){int start = left ;int end = right;if(start>=end){return;}while(left <= right){int pivot = arr[(left + right)/2];while(left<=right && arr[left]<pivot) left++;while(left<=right && arr[right]> pivot) right--;if(left <= right){int temp = arr[right];arr[right] = arr[left];arr[left] = temp;left ++;right--;}}method2(arr,start,right);method2(arr,left,end);}

第二个版本

public static void method1(int[] arr,int left,int right){if(left < right){int i = left -1 ;int pivot = arr[right];for(int j = left ; j< right ;j++){if(arr[j] < pivot){i++;int temp = arr[j];arr[j] = arr[i];arr[i] = temp;}}int pivotIndex = i + 1;int temp = arr[right];arr[right] = arr[pivotIndex];arr[pivotIndex] = temp;method1(arr,left,pivotIndex-1);method1(arr,pivotIndex+1,right);}}