什么是窗口?就是符合题目要求的区域内的数据,将每次符合数据的窗口内的数据记录下来,然后将窗口后移,寻找其他符合要求的数据,每次进入窗口和退出窗口都需要一定的要求
一、长度最小的子数组
LCR 008. 长度最小的子数组 - 力扣(LeetCode)

思路

代码
class Solution {
public:bool istarget(int x, int target){if (x >= target)return true;return false;}int minSubArrayLen(int target, vector<int>& nums) {//先判断是否有总和是否大于target,如果不是那么就直接返回0int judgesum = 0;for (auto e : nums){judgesum += e;}if (judgesum < target)return 0;int len = nums.size(), left = 0, right = 0;//开拓一个数组,放入符合条件的长度,之后进行遍历,进行排序,然后返回最小值vector<int> ans;int sum = 0;while (left < len && right < len){sum += nums[right];if (istarget(sum,target))//如果超过了{while (sum>=target){ans.push_back(right - left + 1);sum -= nums[left];++left;}++right;} else//不满足,那么右指针往后走 {++right;}}sort(ans.begin(), ans.end());return ans[0];}
};二、无重复字符的最长子串
LCR 016. 无重复字符的最长子串 - 力扣(LeetCode)

思路
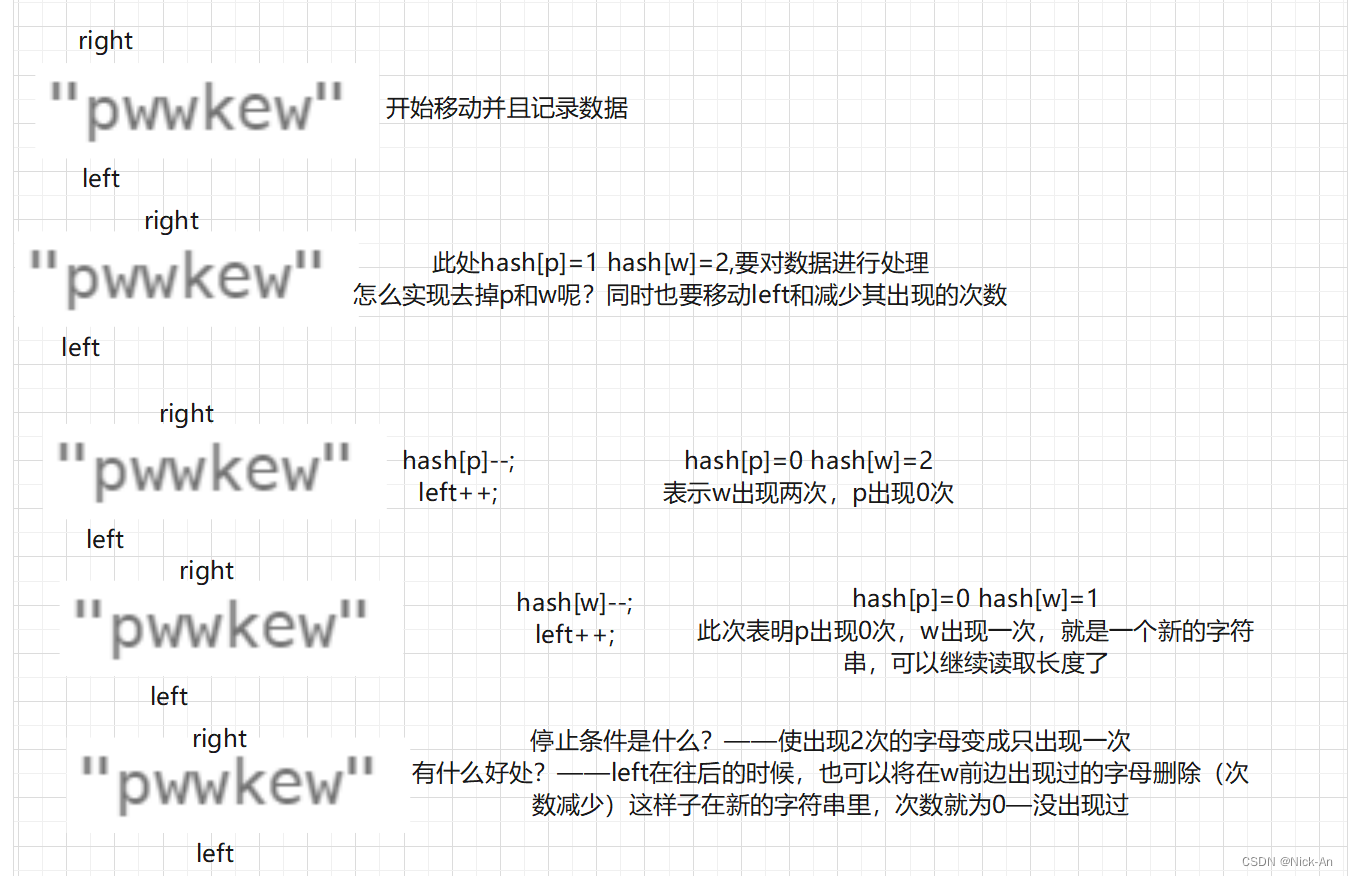
照常还是使用滑动窗口,符合要求的就进入窗口并且记录,不符合要求的就出窗口
这道题的重点就是在于如何判断已经出现过的字母——需要用到哈希表

但是这里会有特殊情况
若是在中间地方出现了重复的,例如pwwke,那么我们前边的pw这两个字母都不要了,重新统计
代码
int lengthOfLongestSubstring(string s) {unordered_map<char,int> mp;int l=0,r=0;int ans=0;while(r<s.size()){mp[s[r]]++;//右指针对应的下标的字母个数往上加while(mp[s[r]]==2)//如果对应的字母出现两次了,说明这时候就要更新开头的位置,并且要将其对应的字母的个数要重置,避免多余的删除{mp[s[l++]]--;}ans=max(ans,r-l+1);//每一次都要更新最长的长度r++;//右指针往后}return ans;}三、最大连续1的个数Ⅲ
1004. 最大连续1的个数 III - 力扣(LeetCode)

思路
这个题目其实可以暴力枚举,但是枚举终究是会超时的,那我们需要用什么来减少时间复杂度?
——滑动窗口

此处的重点是在于将统计翻转后连续1的个数——>一个连续数组里0的个数
然后,我们要注意
当0的个数=k的时候,不是立刻停止读取,而是要判断0下一个数字是否为0,若为0,那就停止right的移动。
若为1,那么right往后的话,连续数组里0的个数还是没有超过k,也就是翻转的次数没有超过k。
为了方便,我选择了当统计0的个数>3的时候,也就是读取到多余的一个0的时候,就开始移动窗口。
并且此题与上两题不同的是,这题是实时记录长度,其他两题是进入窗口后才进行数据的记录
代码
class Solution {
public:int longestOnes(vector<int>& nums, int k) {int ret=0;for(int left=0,right=0,zero=0;right<nums.size();right++){if(nums[right]==0)zero++;while(zero>k){if(nums[left++]==0)zero--; }ret=max(ret,right-left+1);}return ret;}
};四、将x减到0的最小操作数
1658. 将 x 减到 0 的最小操作数 - 力扣(LeetCode)

思路
这道题还是按照滑动窗口,但是题目中给到“移除数组最左端或最右边的元素”。
左右遍历是可以的,但会使代码量及其复杂,我们是否可以换个思路——找到连续的数组使其符合什么关系?

所以我们的思路就转换为——找到连续的数组,使其总和为sum-x,并且找到其最长的长度
代码
int minOperations(vector<int>& nums, int x) {int len=nums.size(),sum=0;for(auto e:nums){sum+=e;}int target=sum-x;int left=0,right=0,maxlen=-1,testsum=0;while(left<len&&right<len){testsum+=nums[right];if(testsum==target){maxlen=max(maxlen,right-left+1);++right;}if(testsum>target){while(testsum>target&&left<len){testsum-=nums[left++];}//去重后也需要进行一个判断if(testsum==target){maxlen=max(maxlen,right-left+1);++right;}}if(testsum<target){++right;}}if (maxlen == -1)//若还为-1,说明没有找到return -1;return (len-maxlen);//总长度减去连续的最长长度,便是两端最短的长度}未完待续.....