上链接:P4147 玉蟾宫 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)![]() https://www.luogu.com.cn/problem/P4147
https://www.luogu.com.cn/problem/P4147
上题干:
有一个NxM的矩阵,每个格子里写着R或者F。R代表障碍格子,F代表无障碍格子请找出其中的一个子矩阵,其元素均为‘F’,并且面积最大,输出它的面积*3的值
求最大子矩阵我们一般用到一个方法叫——悬线法;
下面来介绍悬线法:
我们找任意找一个非障碍格子作为底边的一个格子,从该点出发,引出3条直线,左直线,右直线,上直线。
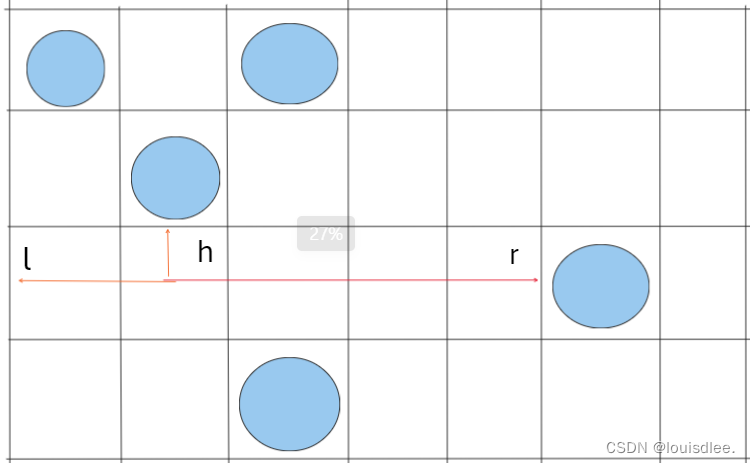
我们从这个点出发,向左一直延伸直到遇到障碍格,向右一直延伸一直延长到障碍格子,同理,向上也是。
第一步:
设置四个数组:
棋盘:char a[N][N];
左悬线数组:表示每个格子能向左延伸到的最远距离, int l[N][N];
右悬线 :表示每个格子能向右延伸到的最远距离,int r[N][N] ;
上悬线:表示每个格子能向上延伸到的最远距离 int h[N][N];
第二步:
求左悬线:
思路:
我们先将每个格子的向左能延伸到的最远距离初始化为该格子本身的列数,也就是它一开始只能延伸到它本身。
以第一行为例:

然后循环每一列,从最左边开始,当a[i][j]为空地,并且a[i][j-1]为空地的时候,该格子的左悬线能延伸到的位置就是左边一格能延伸到的位置。
所以有此代码:
for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)if (a[i][j] == 'F' and a[i][j - 1] == 'F')l[i][j] = l[i][j - 1];
这样就可以求出所有格子的左悬线了。
同理
求右悬线:
思路:
我们先将每个格子的向右能延伸到的最远距离初始化为该格子本身的列数,也就是它一开始只能延伸到它本身
循环每一列,从最右边开始,当a[i][j]为空地,并且a[i][j+1]为空地的时候,该格子的右悬线能延伸到的位置就是右边一格能延伸到的位置。
for (int i = 1; i <= n; i++)for (int j = m; j >= 1; j--)if (a[i][j] == 'F' and a[i][j + 1] == 'F')r[i][j] = r[i][j + 1];求上悬线:
思路:
我们先将每个格子的向上能延伸到的最远距离初始化为该格子本身的高度,即为1,也就是它一开始只能延伸到它本身
循环每一列,从任意一遍开始都行,我们以从左边开始为例子,当a[i][j]为空地,并且a[i-1][j]为空地的时候,该格子的上悬线能延伸到的位置就是上边一格能延伸到的位置。
for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)if (a[i][j] == 'F' and a[i - 1][j] == 'F')h[i][j] = h[i - 1][j] + 1;将这三个代码整合起来就是这样的:
for (int i = 1; i <= n; i++)
{for (int j = 1; j <= m; j++)if (a[i][j] == 'F' and a[i][j - 1] == 'F')l[i][j] = l[i][j - 1];for (int j = m; j >= 1; j--)if (a[i][j] == 'F' and a[i][j + 1] == 'F')r[i][j] = r[i][j + 1];for (int j = 1; j <= m; j++)if (a[i][j] == 'F' and a[i - 1][j] == 'F')h[i][j] = h[i - 1][j] + 1;
}第三步:
求每个格子以上悬线为高的矩形面积
到这里还没有结束,不要傻乎乎的就用每一个格子的三个悬线开始计算面积了。
我们应该可以注意到,有这样一种情况:

如果直接拿右悬线-左悬线 乘以高的话,求出来的面积 是绿色矩形的面积,然而实际上我们希望求的是在上悬线尽可能高的情况下的矩形面积(目的是使得枚举不重不漏)。
所以我们还需要修改一个条件,该格的左悬线应该为 (该格,和上面一格)的左悬线之间长度小的那一根。
由于l[i][j]代表的是该格向左能延伸到的最远的坐标(离得越远,坐标越小),所以我们需要让l[i][j]尽可能大,
同理,我们要让r[i][j]尽可能的小。
那么则有:
for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++) if (a[i][j] == 'F' and a[i - 1][j] == 'F') {r[i][j] = min(r[i][j], r[i - 1][j]);l[i][j] = max(l[i][j], l[i - 1][j]);}到这里就基本结束了。
第四步:
最后我们只需要打擂台,不断求出每个格子三悬线组成的面积的最大值就可以了。
也就是:
for (int i = 1; i <= n; i++) if (a[i][j] == 'F')ans = max(ans, h[i][j] * (r[i][j] - l[i][j] + 1));
总的来看,这道题一共有四个步骤,设三条悬线,求三条悬线,求以上悬线为高的矩形面积,打擂台求最大值。
上代码:
const int N = 1010;
int n, m, ans;
char a[N][N];
int h[N][N], l[N][N], r[N][N];
int main()
{ans = 0;cin >> n >> m;for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++){cin >> a[i][j];h[i][j] = 1, r[i][j] = l[i][j] = j;//初始化h,r,l}for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++)if (a[i][j] == 'F' and a[i][j - 1] == 'F')l[i][j] = l[i][j - 1];for (int j = m; j >= 1; j--)if (a[i][j] == 'F' and a[i][j + 1] == 'F')r[i][j] = r[i][j + 1];for (int j = 1; j <= m; j++)if (a[i][j] == 'F' and a[i - 1][j] == 'F')h[i][j] = h[i - 1][j] + 1;}for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++) {if (a[i][j] == 'F' and a[i - 1][j] == 'F') {r[i][j] = min(r[i][j], r[i - 1][j]);l[i][j] = max(l[i][j], l[i - 1][j]);}if (a[i][j] == 'F')ans = max(ans, h[i][j] * (r[i][j] - l[i][j] + 1));}}cout << 3 * ans;}